2020-2021學(xué)年黑龍江省牡丹江市三校聯(lián)誼高一（下）期中數(shù)學(xué)試卷

一、選擇題：本大題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一個(gè)選項(xiàng)是符合題目要求的。

• 1．設(shè)i是虛數(shù)單位，則復(fù)數(shù)

  2

  i

  1

  -

  i

  在復(fù)平面內(nèi)對(duì)應(yīng)的點(diǎn)位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  組卷：4031引用：57難度：0.9

  解析

• 2．已知△ABC中，內(nèi)角A，B，C的對(duì)邊分別為a,b,c,c=3，a=2，C=120°，則sinA=（　　）

  A． 3 6

  B． 3 3

  C． 1 6

  D． 1 3
  組卷：90引用：4難度：0.7

  解析

• 3．復(fù)數(shù)z=（1+i）（2-i）的共軛復(fù)數(shù)為（　　）

  A．-1+2i

  B．-1-2i

  C．3+i

  D．3-i
  組卷：5引用：2難度：0.8

  解析

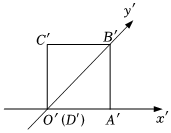• 4．如圖，正方形A'B'C'D'的邊長(zhǎng)為1，它是一個(gè)水平放置的平面圖形的直觀圖，原圖形的面積為（　　）

  A． 4 2

  B． 2 2

  C． 2

  D． 2 2
  組卷：71引用：4難度：0.8

  解析

• 5．已知z=

  （

  1

  +

  3

  i

  ）

  （

  3

  -

  i

  ）

  2

  3

  -

  4

  i

  ，則|z|=（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：4引用：1難度：0.8

  解析

• 6．已知燈塔A在海洋觀察站C的北偏東65°，距離海洋觀察站C的距離為akm,燈塔B在海洋觀察站C的南偏東55°，距離海洋觀察站C的距離為3akm,則燈塔A與燈塔B的距離為（　　）

  A．a(chǎn)km

  B． 3 akm

  C． 7 akm

  D．2akm
  組卷：50引用：3難度：0.7

  解析

• 7．如圖，四邊形ABCD為平行四邊形，

  AE

  =

  1

  2

  AB

  ，

  DF

  =

  1

  2

  FC

  ，若

  DE

  =

  λ

  AC

  +

  μ

  AF

  ，則λ+μ的值為（　　）

  A． 1 2

  B． 2 3

  C． - 1 3

  D．-1
  組卷：617引用：5難度：0.6

  解析

四、解答題：本題共6小題，共70分。解答應(yīng)寫出必要的文字說明、證明過程及演算步驟。

• 21．已知單位向量

  a

  與

  b

  的夾角是鈍角，當(dāng)t∈R時(shí)，|

  a

  -t

  b

  |的最小值為

  3

  2

  ．
  （1）求向量

  a

  與

  b

  的夾角；
  （2）若

  c

  =λ

  a

  +（1-λ）

  b

  ，其中λ∈R，求|

  c

  |的最小值．
  組卷：65引用：2難度：0.6

  解析

• 22．如圖，在三棱臺(tái)ABC-DEF中，平面ABED⊥平面BCFE，BA⊥BC，BC=3，BE=DE=DA=

  1

  2

  AB=1．
  （Ⅰ）求證：AE⊥平面BCFE；
  （Ⅱ）求直線DF與平面AEF所成角的正弦值．
  組卷：220引用：3難度：0.5

  解析