2021-2022學年四川省資陽市安岳縣興隆中學七年級（下）期中數學試卷

一、選擇題。（本大題共10個小題，每小題4分，共40分。在每小題給出的四個選項中，只有一個選項是符合題目的要求的。）

• 1．若x=-3是方程2（x-m）=6的解，則m的值為（　　）

  A．6

  B．-6

  C．12

  D．-12
  組卷：2145引用：29難度：0.9

  解析

• 2．不等式組

  x - 1 ＞ 0

  4 - 2 x ≥ 0

  的解集在數軸上表示為（　　）

  A．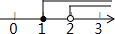

  B．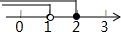

  C．

  D．
  組卷：495引用：15難度：0.9

  解析

• 3．若a＞b,則下列不等式中，不成立的是（　　）

  A．a+5＞b+5

  B．a-5＞b-5

  C．5a＞5b

  D．-5a＞-5b
  組卷：280引用：14難度：0.9

  解析

• 4．若方程3（2x-1）=3x的解與關于x的方程6-2a=2（x+3）的解相同，則a的值為（　　）

  A．2

  B．-2

  C．1

  D．-1
  組卷：373引用：4難度：0.9

  解析

• 5．一球鞋廠，現打折促銷賣出330雙球鞋，比上個月多賣10%，設上個月賣出x雙，列出方程（　　）

  A．10%x=330	B．（1-10%）x=330
  C．（1-10%）2x=330	D．（1+10%）x=330
  組卷：4886引用：29難度：0.7

  解析

• 6．若關于x的不等式組

  x - m ＞ 0

  x + 3 ＞ 2 （ x + 2 ）

  無解，則m的取值范圍為（　　）

  A．m≥-1

  B．m＞-1

  C．m≤-1

  D．m＜-1
  組卷：328引用：2難度：0.7

  解析

• 7．若購買甲商品3件，乙商品2件，丙商品1件，共需140元；購買甲商品1件，乙商品2件，丙商品3件，共需100元；那么購買甲商品1件，乙商品1件，丙商品1件，共需（　　）元．

  A．50

  B．60

  C．70

  D．80
  組卷：396引用：6難度：0.7

  解析

• 8．8個一樣大小的長方形恰好拼成一個大的長方形（如圖），若大長方形的寬為8cm,則每一個小長方形的面積為（　　）

  A．8cm2

  B．15cm2

  C．16cm2

  D．20cm2
  組卷：541引用：18難度：0.9

  解析

三、解答題。

• 24．使方程（組）與不等式（組）同時成立的未知數的值稱為此方程（組）和不等式（組）的“理想解”．
  例：已知方程2x-3=1與不等式x+3＞0，當x=2時，2x-3=2×2-3=1，x+3=2+3=5＞0同時成立，則稱“x=2”是方程2x-3=1與不等式x+3＞0的“理想解”．
  （1）已知①x-

  1

  2

  ＞

  3

  2

  ，②2（x+3）＜4，③

  x

  -

  1

  2

  ＜

  3

  ，試判斷方程2x+3=1的解是否為它與它們中某個不等式的“理想解”；
  （2）若

  x = x 0

  y = y 0

  是方程x-2y=4與不等式組

  x ＞ 3

  y ＜ 1

  的“理想解”，求x₀+2y₀的取值范圍；
  （3）當實數a、b、c滿足a＜b＜c且a+b+c=0時，x=m恒為方程ax=c與不等式組

  x - 1 ≥ t + s

  4 x - 4 ≤ 2 t + s

  的“理想解”，求t、s的取值范圍．
  組卷：485引用：4難度：0.4

  解析

• 25．如圖1，在長方形ABCD中，AB=12cm,BC=6cm,點P沿AB邊從點A開始向點B以2cm/s的速度移動；點Q沿DA邊從點D開始向點A以1厘米/秒的速度移動．如果P、Q同時出發，用t（秒）表示移動的時間．
  （1）當t為何值時，線段AQ的長度等于線段AP的長度？
  （2）當t為何值時，AQ與AP的長度之和是長方形周長的

  1

  4

  ？
  （3）如圖2，P、Q到達B、A后繼續運動，P點到達C點后都停止運動．當t為何值時，線段AQ的長等于線段CP的長的一半？
  組卷：30引用：3難度：0.2

  解析