2016-2017學(xué)年江蘇省蘇州市浮橋中學(xué)八年級(jí)(上)國(guó)慶數(shù)學(xué)作業(yè)(全等三角形)
發(fā)布:2024/4/20 14:35:0
一、選擇題(每題3分,共24分)
-
 1.如圖,OA=OB,OC=OD,∠O=50°,∠D=35°,則∠AEC等于( )
1.如圖,OA=OB,OC=OD,∠O=50°,∠D=35°,則∠AEC等于( )A.60° B.50° C.45° D.30° 組卷:843引用:109難度:0.9 -
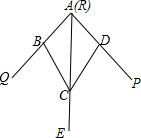 2.如圖,小敏做了一個(gè)角平分儀ABCD,其中AB=AD,BC=DC.將儀器上的點(diǎn)A與∠PRQ的頂點(diǎn)R重合,調(diào)整AB和AD,使它們分別落在角的兩邊上,過(guò)點(diǎn)A,C畫(huà)一條射線AE,AE就是∠PRQ的平分線.此角平分儀的畫(huà)圖原理是:根據(jù)儀器結(jié)構(gòu),可得△ABC≌△ADC,這樣就有∠QAE=∠PAE.則說(shuō)明這兩個(gè)三角形全等的依據(jù)是( )
2.如圖,小敏做了一個(gè)角平分儀ABCD,其中AB=AD,BC=DC.將儀器上的點(diǎn)A與∠PRQ的頂點(diǎn)R重合,調(diào)整AB和AD,使它們分別落在角的兩邊上,過(guò)點(diǎn)A,C畫(huà)一條射線AE,AE就是∠PRQ的平分線.此角平分儀的畫(huà)圖原理是:根據(jù)儀器結(jié)構(gòu),可得△ABC≌△ADC,這樣就有∠QAE=∠PAE.則說(shuō)明這兩個(gè)三角形全等的依據(jù)是( )A.SAS B.ASA C.AAS D.SSS 組卷:5711引用:83難度:0.9 -
3.已知△A1B1C1,△A2B2C2的周長(zhǎng)相等,現(xiàn)有兩個(gè)判斷:
①若A1B1=A2B2,A1C1=A2C2,則△A1B1C1≌△A2B2C2;
②若∠A1=∠A2,∠B1=∠B2,則△A1B1C1≌△A2B2C2,
對(duì)于上述的兩個(gè)判斷,下列說(shuō)法正確的是( )A.①正確,②錯(cuò)誤 B.①錯(cuò)誤,②正確 C.①,②都錯(cuò)誤 D.①,②都正確 組卷:6212引用:78難度:0.4 -
 4.如圖,已知點(diǎn)A、D、C、F在同一條直線上,AB=DE,BC=EF,要使△ABC≌△DEF,還需要添加一個(gè)條件是( )
4.如圖,已知點(diǎn)A、D、C、F在同一條直線上,AB=DE,BC=EF,要使△ABC≌△DEF,還需要添加一個(gè)條件是( )A.∠BCA=∠F B.∠B=∠E C.BC∥EF D.∠A=∠EDF 組卷:2335引用:119難度:0.9 -
 5.如圖,已知∠1=∠2,AC=AD,增加下列條件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED成立的條件有( )
5.如圖,已知∠1=∠2,AC=AD,增加下列條件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED成立的條件有( )A.4個(gè) B.3個(gè) C.2個(gè) D.1個(gè) 組卷:3356引用:174難度:0.7 -
 6.如圖,△ABD與△ACE均為正三角形,且AB<AC,則BE與CD之間的大小關(guān)系是( )
6.如圖,△ABD與△ACE均為正三角形,且AB<AC,則BE與CD之間的大小關(guān)系是( )A.BE=CD B.BE>CD C.BE<CD D.大小關(guān)系不確定 組卷:374引用:21難度:0.9 -
 7.如圖,在△ABC中,AB=AC,∠ABC、∠ACB的平分線BD,CE相交于O點(diǎn),且BD交AC于點(diǎn)D,CE交AB于點(diǎn)E.某同學(xué)分析圖形后得出以下結(jié)論:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE;上述結(jié)論一定正確的是( )
7.如圖,在△ABC中,AB=AC,∠ABC、∠ACB的平分線BD,CE相交于O點(diǎn),且BD交AC于點(diǎn)D,CE交AB于點(diǎn)E.某同學(xué)分析圖形后得出以下結(jié)論:①△BCD≌△CBE;②△BAD≌△BCD;③△BDA≌△CEA;④△BOE≌△COD;⑤△ACE≌△BCE;上述結(jié)論一定正確的是( )A.①②③ B.②③④ C.①③⑤ D.①③④ 組卷:721引用:58難度:0.9 -
 8.如圖所示,已知△ABC和△DCE均是等邊三角形,點(diǎn)B,C,E在同一條直線上,AE與BD與BD交于點(diǎn)O,AE與CD交于點(diǎn)G,AC與BD交于點(diǎn)F,連接OC,F(xiàn)G,其中正確結(jié)論的個(gè)數(shù)是( )
8.如圖所示,已知△ABC和△DCE均是等邊三角形,點(diǎn)B,C,E在同一條直線上,AE與BD與BD交于點(diǎn)O,AE與CD交于點(diǎn)G,AC與BD交于點(diǎn)F,連接OC,F(xiàn)G,其中正確結(jié)論的個(gè)數(shù)是( )
①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.A.1個(gè) B.2個(gè) C.3個(gè) D.4個(gè) 組卷:1054引用:40難度:0.5
三、解答題(共76分)
-
 24.兩個(gè)大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一條直線上,連接DC.
24.兩個(gè)大小不同的等腰直角三角形三角板如圖1所示放置,圖2是由它抽象出的幾何圖形,AB=AC,AE=AD,∠BAC=∠EAD=90°,B,C,E在同一條直線上,連接DC.
(1)請(qǐng)找出圖2中與△ABE全等的三角形,并給予證明(說(shuō)明:結(jié)論中不得含有未標(biāo)識(shí)的字母);
(2)證明:DC⊥BE.組卷:1239引用:54難度:0.5 -
25.問(wèn)題背景:
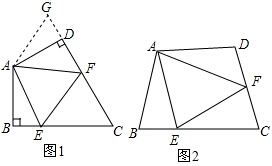
(1)如圖1:在四邊形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F(xiàn)分別是BC,CD上的點(diǎn).且∠EAF=60°.探究圖中線段BE,EF,F(xiàn)D之間的數(shù)量關(guān)系.小王同學(xué)探究此問(wèn)題的方法是,延長(zhǎng)FD到點(diǎn)G.使DG=BE.連接AG,先證明△ABE≌△ADG,再證明△AEF≌△AGF,可得出結(jié)論,他的結(jié)論應(yīng)是 .
探索延伸:
(2)如圖2,若在四邊形ABCD中,AB=AD,∠B+∠D=180°.E,F(xiàn)分別是BC,CD上的點(diǎn),且∠EAF=∠BAD,上述結(jié)論是否仍然成立,并說(shuō)明理由.12組卷:7075引用:43難度:0.5


