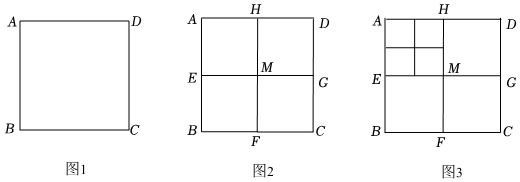
將正方形ABCD(如圖1)作如下劃分,第1次劃分:分別連接正方形ABCD對邊的中點(如圖2),得線段HF和EG,它們交于點M,此時圖2中共有5個正方形;第2次劃分:將圖2左上角正方形AEMH再劃分,得圖3,則圖3中共有9個正方形;
(1)若把左上角的正方形依次劃分下去,則第100次劃分后,圖中共有401401個正方形;
(2)繼續劃分下去,第n次劃分后圖中共有4n+14n+1個正方形;
(3)能否將正方形ABCD劃分成有2018個正方形的圖形?如果能,請算出是第幾次劃分,如果不能,需說明理由.
(4)如果設原正方形的邊長為1,通過不斷地分割該面積為1的正方形,并把數量關系和幾何圖形巧妙地結合起來,可以很容易得到一些計算結果,試著探究求出下面表達式的結果.計算34(1+14+142+143+……+14n)(直接寫出答案即可)
3
4
1
4
1
4
2
1
4
3
1
4
n
【考點】規律型:圖形的變化類.
【答案】401;4n+1
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/20 4:0:1組卷:273引用:5難度:0.7
相似題
-
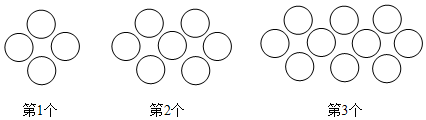
1.觀察下列圖形的構成規律,按此規律,第20個圖形中棋子的個數為 .
 發布:2025/6/25 6:30:1組卷:53引用:2難度:0.5
發布:2025/6/25 6:30:1組卷:53引用:2難度:0.5 -
2.在同一平面內的n條直線兩兩相交,最多共有28個交點,則n=.
發布:2025/6/24 21:0:1組卷:216引用:5難度:0.7 -
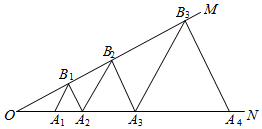 3.如圖,∠MON=30°,點A1,A2,A3,A4,…在射線ON上,點B1,B2,B3,…在射線OM上,且△A1B1A2,△A2B2A3,△A3B3A4,…均為等邊三角形,以此類推,若OA1=1,則△A2021B2021A2022的邊長為.發布:2025/6/25 8:30:1組卷:663引用:9難度:0.5
3.如圖,∠MON=30°,點A1,A2,A3,A4,…在射線ON上,點B1,B2,B3,…在射線OM上,且△A1B1A2,△A2B2A3,△A3B3A4,…均為等邊三角形,以此類推,若OA1=1,則△A2021B2021A2022的邊長為.發布:2025/6/25 8:30:1組卷:663引用:9難度:0.5


