2021-2022學年河南省信陽市高三(上)開學數學試卷(理科)
發布:2025/6/29 0:0:12
一、選擇題:本題共12小題,每小題5分,共60分。在每小題給出的四個選項中,只有一項是符合題目要求的。
-
1.已知復數z滿足
,則z2=( )iz=32+12iA. 12+32iB. 12-32iC. -12-32iD. -12+32i組卷:143引用:4難度:0.8 -
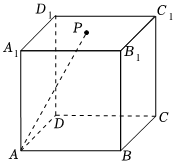 2.如圖,點P是棱長為2的正方體ABCD-A1B1C1D1表面上的一個動點,直線AP與平面ABCD所成的角為45°,則點P的軌跡長度為?( )
2.如圖,點P是棱長為2的正方體ABCD-A1B1C1D1表面上的一個動點,直線AP與平面ABCD所成的角為45°,則點P的軌跡長度為?( )A. π+42B. 42πC. 23D. 32+π組卷:459引用:4難度:0.6 -
3.已知集合A={x∈N|x2<8x},B={2,3,6},C={2,3,7},則B∪(?AC)=( )
A.{2,3,4,5} B.{2,3,4,5,6} C.{1,2,3,4,5,6} D.{1,3,4,5,6,7} 組卷:59引用:5難度:0.8 -
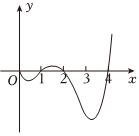 4.已知奇函數f(x)在[0,+∞)上的部分圖象如圖所示,則不等式f(x)≥0在[-4,4]上的解集為( )
4.已知奇函數f(x)在[0,+∞)上的部分圖象如圖所示,則不等式f(x)≥0在[-4,4]上的解集為( )A.[-4,-2]∪[1,2]∪{4} B.[-3,-2]∪[-1,0]∪[1,2]∪{-4,4} C.[-2,-1]∪[1,2]∪{-4,4} D.[-4,-2]∪[-1,0]∪[1,2]∪{4} 組卷:15引用:1難度:0.8 -
5.從甲、乙等6名志愿者中隨機選3名參加社區服務工作,則甲、乙都入選的概率為( )
A. 16B. 15C. 14D. 13組卷:70引用:1難度:0.7 -
6.如圖,直線y=ax-
的圖象可能是( )1aA. 
B. 
C. 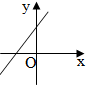
D. 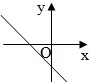 組卷:74引用:10難度:0.9
組卷:74引用:10難度:0.9 -
7.已知橢圓
,過橢圓左焦點的直線與橢圓相交于A,B兩點,直線l的傾斜角為60°,且x2a2+y2b2=1(a>b>0),則橢圓的離心率為( )FA=2BFA. 25B. 22C. 12D. 23組卷:50引用:1難度:0.6 -
8.若x,y滿足
,且z=y-x的最小值為-4,則k的值為( )x+y-2≥0kx-y+2≥0y≥0A.2 B.-2 C. 12D.- 12組卷:2158引用:56難度:0.7 -
9.已知
為自然對數的底數),a=ln22,b=1e(e,則a,b,c的大小關系為( )c=ln63A.a>b>c B.a>c>b C.b>a>c D.b>c>a 組卷:168引用:2難度:0.6 -
10.設函數
,若f(x)=2lnxx,x>0sin(ωx+π6),-π≤x≤0恰有5個不同零點,則正實數ω的范圍為( )y=f(x)-12A. (103,4]B. [103,4)C. (2,103]D. [2,103)組卷:62引用:3難度:0.5 -
11.已知直線l,m和平面α,β,下列命題正確的是( )
A.m∥l,l∥α?m∥α B.l∥β,m∥β,l?α,m?α?α∥β C.l∥m,l?α,m?β?α∥β D.l∥β,m∥β,l?α,m?α,l∩m=M?α∥β 組卷:24引用:1難度:0.6 -
12.為了得到函數y=sin 3x+cos 3x+1的圖象,可以將函數y=
sin 3x的圖象( )2A.向右平移 個單位,向下平移1個單位π12B.向左平移 個單位,向下平移1個單位π12C.向右平移 個單位,向上平移1個單位π12D.向左平移 個單位,向上平移1個單位π12組卷:304引用:6難度:0.7
二、填空題:本題共4小題,每小題5分,共20分。
-
13.在△ABC中,若AB=2,∠B=
,∠C=5π12,則BC=.π4組卷:675引用:5難度:0.8 -
14.已知直線l:y=2x-10與雙曲線
的一條漸近線平行,且經過雙曲線的一個焦點,則雙曲線的標準方程為 .x2a2-y2b2=1(a>0,b>0)組卷:174引用:3難度:0.6 -
15.若向量
,且a=(1,m),b=(2n,10),則mn=.a∥b組卷:14引用:2難度:0.8 -
16.用過球心的平面將一個球分成兩個半球,則一個半球的表面積與原來整球的表面積之比為.
組卷:25引用:3難度:0.7
三、解答題:共70分。解答應寫出文字說明、證明過程或演算步驟,第17~21題為必考題,每個試題考生都必須作答,第22、23題為選考題,考生根據要求作答。(一)必考題:共60分。
-
17.在10件產品中,有3件一等品,4件二等品,3件三等品.從這10件產品中任取3件,求:
(I)取出的3件產品中一等品件數X的分布列和數學期望;
(II)取出的3件產品中一等品件數多于二等品件數的概率.組卷:704引用:13難度:0.1 -
18.已知函數f(x)=x3-x,g(x)=2x-3.
(Ⅰ)求曲線y=f(x)在點(1,f(1))處的切線方程;
(Ⅱ)求函數f(x)在[0,2]上的最大值;
(Ⅲ)求證:存在唯一的x0,使得f(x0)=g(x0).組卷:117引用:9難度:0.3 -
19.在直角坐標系xOy中,直線l的參數方程為
(t為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為ρ=2sinθ.x=3+ty=5+3t
(1)求直線l的普通方程及曲線C的直角坐標方程;
(2)設點M的直角坐標為(,5),直線l與曲線C交于A,B兩點,求3的值.1|MA|+1|MB|組卷:129引用:2難度:0.5 -
20.已知數列{an}的首項a1=1且滿足
.4anan+1=an-3an+1(n∈N*)
(1)證明:是等比數列;{1an+2}
(2)數列{bn}滿足,b1=13,記bn+1=2n+12n+3bn,求數列{cn}的前n項和Tn.cn=2an+1anbn組卷:402引用:8難度:0.5 -
21.在平面直角坐標系xOy中,F1(-3,0),F2(3,0),點P是平面上一點,使△PF1F2的周長為16.求點P的軌跡方程.
組卷:7引用:1難度:0.5
(二)選考題:共10分。請考生在第22、23題中任選一題作答,如果多做,則按所做的第一題計分。[選修4-4:坐標系與參數方程]
-
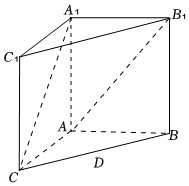 22.如圖,在直三棱柱ABC-A1B1C1中,AA1=AC=4,AB=3,BC=5,點D是線段BC的中點.
22.如圖,在直三棱柱ABC-A1B1C1中,AA1=AC=4,AB=3,BC=5,點D是線段BC的中點.
(1)求證:AB⊥A1C;
(2)求二面角D-CA1-A的余弦值.組卷:339引用:6難度:0.6
[選修4-5:不等式選講]
-
23.已知a>0,b>0,c>0,
+1a3+1b3+3abc的最小值為m.1c3
(Ⅰ)求m的值;
(Ⅱ)解關于x的不等式|x+1|-2x<m.組卷:29引用:4難度:0.6


