當前位置：試卷中心 > 試卷詳情

2022-2023學年河南省許昌市禹州高級中學菁華校區高二（上）測評數學試卷（1月份）

發布：2025/6/29 1:0:12

一、單項選擇題：

1．若兩圓x²+y²+2
m
x+m-4=0（m＞0）和x²+y²-4
n
y-1+4n=0（n＞0）恰有三條公切線，則
1
m
+
1
n
的最小值為（　　）
A．
1
9
B．
4
9
C．1 D．3
組卷：273引用：4難度：0.5
解析
2．以橢圓
x
2
25
+
y
2
9
=1的左焦點為焦點的拋物線的標準方程是（　　）
A．y²=16x B．y²=-8x C．y²=-16x D．x²=-16y
組卷：212引用：6難度：0.9
解析
3．已知等差數列{a_n}的前n項和為S_n，對任意的n∈N^*，均有S₅≤S_n成立，則
a
8
a
6
的值的取值范圍是（　　）
A．（3，+∞） B．[3，+∞）
C．（-∞，-3）∪[3，+∞） D．（-∞，-3]∪[3，+∞）
組卷：363引用：5難度：0.5
解析
4．已知復數z滿足
3
+
i
z
=
1
-
i
，則|z|=（　　）
A．
5
B．2 C．
3
D．
2
組卷：207引用：5難度：0.5
解析
5．邊長
2
為的正方形ABCD沿對角線BD折成直二面角，E、F分別為AD、BC的中點，O是正方形ABCD的中心，則∠EOF的大小為（　　）
A．60° B．120° C．45° D．135°
組卷：107引用：1難度：0.5
解析
6．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的離心率為
5
，其中一條漸近線與圓（x-2）²+（y-3）²=1交于A，B兩點，則|AB|=（　　）
A．
1
5
B．
5
5
C．
2
5
5
D．
4
5
5
組卷：3126引用：3難度：0.6
解析
7．某中學為提高學生的健康水平，增設了每天40分鐘的體育鍛煉課程，學生可以在跳繩、羽毛球、乒乓球、籃球、排球等課程中選擇一門．為了解該校學生參與乒乓球運動的情況，在全校班級中隨機抽取了7個班（將其編號為1，2，…，7），如表是這7個班參與乒乓球運動的人數統計表：

班編號 1 2 3 4 5 6 7

人數/人 15 10 14 15 9 11 13

若從這7個班中隨機選取2個進行調查研究，則選出的2個班中至少有1個班參與乒乓球運動的人數超過12人的概率為（　　）
A．
4
7
B．
2
3
C．
5
6
D．
6
7
組卷：85引用：2難度：0.7
解析
8．已知O為空間任意一點，A，B，C，P滿足任意三點不共線，但四點共面，且
BP
=m
OA
+
OB
+
OC
，則m的值為（　　）
A．-1 B．2 C．-2 D．-3
組卷：589引用：11難度：0.9
解析
9．橢圓
x
2
16
+
y
2
12
=
1
的離心率為（　　）
A．
1
3
B．
1
2
C．
3
3
D．
2
2
組卷：123引用：2難度：0.9
解析
10．已知 M（-2，0），圓C：x²-4x+y²=0，動圓P經過M點且與圓C相切，則動圓圓心P的軌跡方程是（　　）
A．x²-
y
2
3
=1（x≥1） B．
x
2
3
-y²=1（x≥
3
）
C．x²-
y
2
3
=1 D．
x
2
3
-y²=1
組卷：95引用：2難度：0.7
解析
11．油紙傘是中國傳統工藝品，至今已有1000多年的歷史，為宣傳和推廣這一傳統工藝，北京市文化宮于春分時節開展油紙傘文化藝術節．活動中將油紙傘撐開后擺放在戶外展覽場地上，如圖所示，該傘的傘沿是一個半徑為
2
的圓，圓心到傘柄底端距離為
2
，陽光照射油紙傘在地面形成了一個橢圓形影子（春分時，北京的陽光與地面夾角為60°），若傘柄底端正好位于該橢圓的焦點位置，則該橢圓的離心率為（　　）
A．
2
-
3
B．
2
-
1
C．
3
-
1
D．
2
2
組卷：119引用：10難度：0.5
解析
12．已知集合A={1，2，3}，B={3，4}，則A∩B=（　　）
A．{1，2，3} B．{1，3} C．{3} D．?
組卷：2引用：1難度：0.8
解析

二、填空題：本大題共4小題，每小題5分，共20分.

13．在棱長為a的正方體ABCD-A₁B₁C₁D₁中，向量
B
A
1
與向量
AC
所成的角為
．
組卷：41引用：6難度：0.7
解析
14．雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線方程為y=2x,且焦點到漸近線的距離為2，則該雙曲線的焦距為
．
組卷：128引用：3難度：0.5
解析
15．若4^x=9^y=6，則
1
x
+
1
y
=

．
組卷：2917引用：4難度：0.5
解析
16．有窮等差數列{a_n}的各項均為正數，若a₂₀₂₃=3，則
2
a
2000
+
1
2
a
2046
的最小值是
．
組卷：73引用：3難度：0.6
解析

三、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

17．已知等差數列{a_n}的前四項和為10，且a₂，a₃，a₇成等比數列．
（1）求數列{a_n}通項公式；
（2）設
b
n
=
a
n
+
2
n
，求數列{b_n}的前n項和S_n．
組卷：495引用：12難度：0.7
解析
18．已知圓C經過兩點A（2，2），B（3，3），且圓心C在直線x-y+1=0上．
（1）求圓C的標準方程；
（2）設直線l：y=kx+1與圓C相交于M，N兩點，O為坐標原點，若
OM
?
ON
=
64
5
，求|MN|的值．
組卷：182引用：3難度：0.6
解析
19．已知拋物線C：y²=2px（p＞0）的焦點為F，M（1，y₀）（y₀＞0）是拋物線上一點且三角形MOF的面積為
1
8
（其中O為坐標原點），不過點M的直線l與拋物線C交于P，Q兩點，且以PQ為直徑的圓經過點M，過點M作MN⊥PQ交PQ于點N．
（1）求拋物線C的方程；
（2）求證直線PQ恒過定點，并求出點N的軌跡方程．
組卷：146引用：3難度：0.6
解析
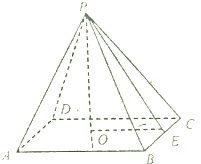20．已知正四棱錐P-ABCD中，AB=6cm,側面與底面ABCD所成角的大小為45°
（1）求正四棱錐的體積；
（2）側棱與底面所成角的大小（精確到1度）
組卷：3引用：0難度：0.9
解析
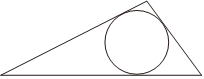21．已知三角形的三邊為a,b,c,設p=
1
2
（a+b+c），求證：
（1）三角形的面積S=
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
．
（2）r為三角形內切圓的半徑，則r=
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
p
．
（3）把邊BC，CA，AB上的高分別記為h_a，h_b，h_c，則．
h_a=
2
a
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
，h_b=
2
b
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
，h_c=
2
c
p
（
p
-
a
）
（
p
-
b
）
（
p
-
c
）
．
組卷：176引用：2難度：0.9
解析
22．從橢圓
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
上一點P向x軸引垂線，垂足恰為橢圓的左焦點F₁，A為橢圓的右頂點，B是橢圓的上頂點，且
AB
=
λ
OP
（
λ
＞
0
）
．
（1）求該橢圓的離心率．
（2）若該橢圓的準線方程是
x
=±
2
5
，求橢圓方程．
組卷：44引用：4難度：0.1
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（3，+∞）	B．[3，+∞）
C．（-∞，-3）∪[3，+∞）	D．（-∞，-3]∪[3，+∞）

A．x²- y 2 3 =1（x≥1）	B． x 2 3 -y²=1（x≥ 3 ）
C．x²- y 2 3 =1	D． x 2 3 -y²=1

班編號	1	2	3	4	5	6	7
人數/人	15	10	14	15	9	11	13

2022-2023學年河南省許昌市禹州高級中學菁華校區高二（上）測評數學試卷（1月份）

一、單項選擇題：

1．若兩圓x2+y2+2mx+m-4=0（m＞0）和x2+y2-4ny-1+4n=0（n＞0）恰有三條公切線，則1m+1n的最小值為（ ）

2．以橢圓x225+y29=1的左焦點為焦點的拋物線的標準方程是（ ）

3．已知等差數列{an}的前n項和為Sn，對任意的n∈N*，均有S5≤Sn成立，則a8a6的值的取值范圍是（ ）

4．已知復數z滿足3+iz=1-i，則|z|=（ ）

5．邊長2為的正方形ABCD沿對角線BD折成直二面角，E、F分別為AD、BC的中點，O是正方形ABCD的中心，則∠EOF的大小為（ ）

6．已知雙曲線x2a2-y2b2=1（a＞0，b＞0）的離心率為5，其中一條漸近線與圓（x-2）2+（y-3）2=1交于A，B兩點，則|AB|=（ ）

8．已知O為空間任意一點，A，B，C，P滿足任意三點不共線，但四點共面，且BP=mOA+OB+OC，則m的值為（ ）

9．橢圓x216+y212=1的離心率為（ ）

10．已知 M（-2，0），圓C：x2-4x+y2=0，動圓P經過M點且與圓C相切，則動圓圓心P的軌跡方程是（ ）

12．已知集合A={1，2，3}，B={3，4}，則A∩B=（ ）

二、填空題：本大題共4小題，每小題5分，共20分.

13．在棱長為a的正方體ABCD-A1B1C1D1中，向量BA1與向量AC所成的角為．

14．雙曲線x2a2-y2b2=1（a＞0，b＞0）的一條漸近線方程為y=2x,且焦點到漸近線的距離為2，則該雙曲線的焦距為 ．

15．若4x=9y=6，則1x+1y= ．

16．有窮等差數列{an}的各項均為正數，若a2023=3，則2a2000+12a2046的最小值是 ．

三、解答題：本大題共6小題，共70分.解答應寫出文字說明，證明過程或演算步驟.

17．已知等差數列{an}的前四項和為10，且a2，a3，a7成等比數列．（1）求數列{an}通項公式；（2）設bn=an+2n，求數列{bn}的前n項和Sn．

18．已知圓C經過兩點A（2，2），B（3，3），且圓心C在直線x-y+1=0上．（1）求圓C的標準方程；（2）設直線l：y=kx+1與圓C相交于M，N兩點，O為坐標原點，若OM?ON=645，求|MN|的值．

20．已知正四棱錐P-ABCD中，AB=6cm,側面與底面ABCD所成角的大小為45°（1）求正四棱錐的體積；（2）側棱與底面所成角的大小（精確到1度）

22．從橢圓x2a2+y2b2=1（a＞b＞0）上一點P向x軸引垂線，垂足恰為橢圓的左焦點F1，A為橢圓的右頂點，B是橢圓的上頂點，且AB=λOP（λ＞0）．（1）求該橢圓的離心率．（2）若該橢圓的準線方程是x=±25，求橢圓方程．

1．若兩圓x²+y²+2
m
x+m-4=0（m＞0）和x²+y²-4
n
y-1+4n=0（n＞0）恰有三條公切線，則
1
m
+
1
n
的最小值為（　　）

2．以橢圓
x
2
25
+
y
2
9
=1的左焦點為焦點的拋物線的標準方程是（　　）

3．已知等差數列{a_n}的前n項和為S_n，對任意的n∈N^*，均有S₅≤S_n成立，則
a
8
a
6
的值的取值范圍是（　　）

4．已知復數z滿足
3
+
i
z
=
1
-
i
，則|z|=（　　）

5．邊長
2
為的正方形ABCD沿對角線BD折成直二面角，E、F分別為AD、BC的中點，O是正方形ABCD的中心，則∠EOF的大小為（　　）

6．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的離心率為
5
，其中一條漸近線與圓（x-2）²+（y-3）²=1交于A，B兩點，則|AB|=（　　）

8．已知O為空間任意一點，A，B，C，P滿足任意三點不共線，但四點共面，且
BP
=m
OA
+
OB
+
OC
，則m的值為（　　）

9．橢圓
x
2
16
+
y
2
12
=
1
的離心率為（　　）

10．已知 M（-2，0），圓C：x²-4x+y²=0，動圓P經過M點且與圓C相切，則動圓圓心P的軌跡方程是（　　）

12．已知集合A={1，2，3}，B={3，4}，則A∩B=（　　）

13．在棱長為a的正方體ABCD-A₁B₁C₁D₁中，向量
B
A
1
與向量
AC
所成的角為
．

14．雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的一條漸近線方程為y=2x,且焦點到漸近線的距離為2，則該雙曲線的焦距為
．

15．若4^x=9^y=6，則
1
x
+
1
y
=

．

16．有窮等差數列{a_n}的各項均為正數，若a₂₀₂₃=3，則
2
a
2000
+
1
2
a
2046
的最小值是
．

17．已知等差數列{a_n}的前四項和為10，且a₂，a₃，a₇成等比數列．
（1）求數列{a_n}通項公式；
（2）設
b
n
=
a
n
+
2
n
，求數列{b_n}的前n項和S_n．

18．已知圓C經過兩點A（2，2），B（3，3），且圓心C在直線x-y+1=0上．
（1）求圓C的標準方程；
（2）設直線l：y=kx+1與圓C相交于M，N兩點，O為坐標原點，若
OM
?
ON
=
64
5
，求|MN|的值．

20．已知正四棱錐P-ABCD中，AB=6cm,側面與底面ABCD所成角的大小為45°
（1）求正四棱錐的體積；
（2）側棱與底面所成角的大小（精確到1度）