2021年西藏拉薩市高考數(shù)學(xué)二模試卷（文科）
發(fā)布：2025/6/29 5:0:12
一、選擇題：本題共12小題，每小題5分，在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。
-
1．若方程
所表示的曲線(xiàn)為C，給出下列四個(gè)命題：x24-t+y2t-1=1
①若C為橢圓，則1＜t＜4；
②若C為雙曲線(xiàn)，則t＞4或t＜1；
③曲線(xiàn)C不可能是圓；
④若，曲線(xiàn)C為橢圓，且焦點(diǎn)坐標(biāo)為1＜t＜52；若t＜1，曲線(xiàn)C為雙曲線(xiàn)，且虛半軸長(zhǎng)為（±5-2t，0）．1-t
則為真命題的是（ ）組卷：18引用：2難度：0.7 -
2．將菱形ABCD沿對(duì)角線(xiàn)AC折起，當(dāng)四面體B-ACD體積最大時(shí)，它的內(nèi)切球和外接球表面積之比為（ ）
組卷：296引用：3難度：0.5 -
3．已知定義在實(shí)數(shù)集R上的函數(shù)f（x）滿(mǎn)足f（1）=3，且f（x）的導(dǎo)數(shù)f′（x）在R上恒有f′（x）＜2（x∈R），則不等式f（x）＜2x+1的解集為（ ）
組卷：413引用：11難度：0.7 -
4．設(shè)集合A={x|x2-9＜0}，B={x|-1＜x≤5}，則A∩B=（ ）
組卷：23引用：2難度：0.9 -
5．樣本中共有5個(gè)個(gè)體，其值分別為x1，x2，x3，x4，x5．若該樣本的平均數(shù)為3，則3x1+1，3x2+1，3x3+1，3x4+1，3x5+1的平均數(shù)為（ ）
組卷：94引用：2難度：0.8 -
6．已知拋物線(xiàn)C：y2=2px（p＞0）經(jīng)過(guò)點(diǎn)M（x0，3），點(diǎn)M到拋物線(xiàn)C的焦點(diǎn)F的距離為3，則拋物線(xiàn)C的準(zhǔn)線(xiàn)方程為（ ）
組卷：181引用：4難度：0.7 -
7．已知數(shù)列{an}為等比數(shù)列，a5=1，a9=81，則a7=（ ）
組卷：806引用：10難度：0.9 -
8．已知
=2，則sinθcosθ的值是（ ）sinθ+cosθsinθ-cosθ組卷：706引用：12難度：0.9 -
9．在菱形ABCD中，與
相等的向量可以是（ ）AB組卷：192引用：4難度：0.7 -
10．設(shè)
，則z的共軛復(fù)數(shù)的虛部為（ ）z=2+i1-i組卷：109引用：4難度：0.8 -
11．國(guó)防部新聞發(fā)言人在2020年9月24日舉行的例行記者會(huì)上指出：“臺(tái)灣是中國(guó)不可分割的一部分，解放軍在臺(tái)海地區(qū)組織實(shí)兵演練，展現(xiàn)的是捍衛(wèi)國(guó)家主權(quán)和領(lǐng)土完整的決心和能力”，如圖為我空軍戰(zhàn)機(jī)在海面上空繞臺(tái)巡航．已知海面上的大氣壓強(qiáng)是760mmHg,大氣壓強(qiáng)p（單位：mmHg）和高度h（單位：m）之間的關(guān)系為p=760e-hk（e是自然對(duì)數(shù)的底數(shù)，k是常數(shù)），根據(jù)實(shí)驗(yàn)知500m高空處的大氣壓強(qiáng)是700mmHg,則我軍戰(zhàn)機(jī)在1000m高空處的大氣壓強(qiáng)約是（結(jié)果保留整數(shù)）（ ）組卷：260引用：9難度：0.9 -
12．系統(tǒng)找不到該試題
二、填空題：本題共4小題，每小題5分。
-
13．若實(shí)數(shù)x、y滿(mǎn)足約束條件
，則z=2x+y的最小值是 ．x+2≤0，x+y+4≥0x-y+2≥0，組卷：13引用：1難度：0.8 -
14．命題“?x＞1，使得x2≥2”的否定是．
組卷：120引用：7難度：0.9 -
15．如圖是一個(gè)正方體的平面展開(kāi)圖，在這個(gè)正方體中，下列說(shuō)法中，正確的序號(hào)是 ．
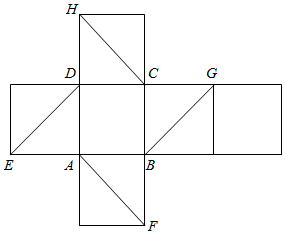
①直線(xiàn)AF與直線(xiàn)DE相交；
②直線(xiàn)CH與直線(xiàn)DE平行；
③直線(xiàn)BG與直線(xiàn)DE是異面直線(xiàn)；
④直線(xiàn)CH與直線(xiàn)BG成60°角．組卷：64引用：5難度：0.7 -
16．已知圓C經(jīng)過(guò)兩點(diǎn)P（-1，-3），Q（2，6），且圓心在直線(xiàn)x+2y-4=0上，若直線(xiàn)l的方程為x+m（y-1）+1=0（m∈R），圓心C到直線(xiàn)l的距離是1，則m的值是 ．
組卷：18引用：2難度：0.8
三、解答題：解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟。
-
，
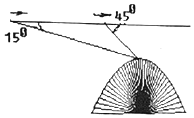17．航空測(cè)量組的飛機(jī)航線(xiàn)和山頂在同一鉛直平面內(nèi)，已知飛機(jī)的高度為海拔10千米，速度為180千米/小時(shí)．飛機(jī)先看到山頂?shù)母┙菫?5°，經(jīng)過(guò)420秒后又看到山頂?shù)母┙菫?5°，求山頂?shù)暮０胃叨龋ㄈ?div dealflag="1" class="MathJye" mathtag="math">2=1.4）．3=1.7
組卷：18引用：3難度：0.5
18．在直角坐標(biāo)系xOy中，曲線(xiàn)C的參數(shù)方程是x=-1+2cosφ y=2sinφ
（φ為參數(shù)），以坐標(biāo)原點(diǎn)為極點(diǎn)，x軸的正半軸為極軸建立極坐標(biāo)系．
（1）求曲線(xiàn)C的極坐標(biāo)方程；
（2）已知曲線(xiàn)C上兩點(diǎn)A，B的極坐標(biāo)分別為A（ρ1，α），B（ρ2，α+π2），求證：ρ12+ρ22+9ρ21+9ρ22=16．
x = - 1 + 2 cosφ |
y = 2 sinφ |
π
2
9
ρ
2
1
+
9
ρ
2
2
組卷：55引用：1難度：0.5
19．為了對(duì)某課題進(jìn)行研究，用分層抽樣方法從三所高校A，B，C的相關(guān)人員中抽取若干人組成研究小組，有關(guān)數(shù)據(jù)見(jiàn)表（單位：人）
| 高校 | 相關(guān)人數(shù) | 抽取人數(shù) |
| A | 18 | x |
| B | 36 | 2 |
| C | 54 | y |
（2）若從高校B、C抽取的人中選2人作專(zhuān)題發(fā)言，求這2人都來(lái)自高校C的概率．
組卷：747引用：47難度：0.5
20．已知函數(shù)g（x）=ax2-（a+2）x,h（x）=lnx,令f（x）=g（x）+h（x）．
（1）當(dāng)a=1時(shí)，求函數(shù)y=g（x）在x=1處的切線(xiàn)方程；
（2）當(dāng)a為正數(shù)且1≤x≤e時(shí)，f（x）min=-2，求a的最小值；
（3）若f（x1）-f（x2）x1-x2＞-2對(duì)一切0＜x1＜x2都成立，求a的取值范圍．
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
組卷：401引用：8難度：0.5
21．證明題：
（1）已知a≥b＞0，求證：2a3-b3≥2ab2-a2b；
（2）求證：a-a-1＜a-2-a-3（其中a≥3）．
a
-
a
-
1
＜
a
-
2
-
a
-
3
組卷：44引用：4難度：0.6
請(qǐng)考生在第22、23題中任選一題作答，如果多做，則按所做的第一題計(jì)分。[選修4-4：坐標(biāo)系與參數(shù)方程]
-
22．已知橢圓C：
的離心率為x2a2+y2b2=1（a＞b＞0），左、右頂點(diǎn)分別為A、B，點(diǎn)P、Q為橢圓上異于A(yíng)、B的兩點(diǎn)，△PAB面積的最大值為2．32
（1）求橢圓C的方程；
（2）設(shè)直線(xiàn)AP、BQ的斜率分別為k1、k2，且3k1=5k2．求證：直線(xiàn)PQ經(jīng)過(guò)定點(diǎn)．組卷：81引用：2難度：0.5
[選修4-5：不等式選講]
-
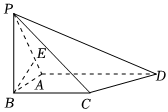23．如圖，在四棱錐P-ABCD中，平面PAB⊥平面ABCD，AB⊥BC，AD∥BC，AD=3，．PA=BC=2AB=2，PB=3
（1）求證：BC⊥PB；
（2）求平面PCD與平面ABCD夾角的余弦值；
（3）棱PA上是否存在點(diǎn)E，它與點(diǎn)B到平面PCD的距離相等，若存在求線(xiàn)段BE的長(zhǎng)；若不存在說(shuō)明理由．組卷：21引用：2難度：0.5