2022-2023學年天津七中高三（上）期中數(shù)學試卷

一、選擇題（本大題共9小題，共45分.在每小題列出的選項中，選出符合題目的一項）

• 1．已知

  a

  =

  lo

  g

  3

  π

  ，

  b

  =

  1

  log

  3

  π

  -

  1

  ，

  c

  =

  1

  2

  -

  log

  3

  π

  ，則（　　）

  A．a(chǎn)＜b＜c

  B．b＜c＜a

  C．c＜a＜b

  D．a(chǎn)＜c＜b
  組卷：86引用：2難度：0.6

  解析

• 2．已知函數(shù)f（x）=tan（ωx-φ）（ω＞0，0＜φ＜π）與直線y=a交于A，B兩點，且線段AB長度的最小值為

  π

  3

  ，若將函數(shù)f（x）的圖象向左平移

  π

  12

  個單位后恰好關(guān)于原點對稱，則φ的最大值為（　　）

  A． π 8

  B． π 4

  C． 3 π 4

  D． 7 π 8
  組卷：244引用：5難度：0.5

  解析

• 3．“中國剩余定理”又稱“孫子定理”，最早可見于我國南北朝時期的數(shù)學著作《孫子算經(jīng)》，1852年，英國傳教士偉烈亞力將該解法傳至歐洲，1874年，英國數(shù)學家馬西森指出此法符合1801年由高斯得到的關(guān)于同余式解法的一般性定理，因而西方稱之為“中國剩余定理”．此定理講的是關(guān)于整除的問題，現(xiàn)將1到2023這2023個數(shù)中，能被7除余1且被9除余1的數(shù)按從小到大的順序排成一列，構(gòu)成數(shù)列{a_n}，則該數(shù)列的和為（　　）

  A．30014

  B．30016

  C．33296

  D．33297
  組卷：24引用：1難度：0.7

  解析

• 4．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  的左、右焦點分別為F₁，F(xiàn)₂．橢圓C在第一象限存在點M，使得|MF₁|=|F₁F₂|，直線F₁M與y軸交于點A，且F₂A是∠MF₂F₁的角平分線，則橢圓C的離心率為（　　）

  A． 6 - 1 2

  B． 5 - 1 2

  C． 1 2

  D． 3 - 1 2
  組卷：225引用：2難度：0.5

  解析

• 5．定義在（0，+∞）上的函數(shù)f（x）滿足

  xf

  ′

  （

  x

  ）

  +

  1

  ＞

  0

  ，

  f

  （

  2

  ）

  =

  ln

  1

  2

  ，則不等式f（e^x）+x＞0的解集為（　　）

  A．（0，2ln2）

  B．（0，ln2）

  C．（ln2，1）

  D．（ln2，+∞）
  組卷：263引用：5難度：0.5

  解析

• 6．函數(shù)y=|cosx|的一個單調(diào)減區(qū)間是（　　）

  A． （ - π 4 ， π 4 ）

  B． （ π 4 ， 3 π 4 ）

  C． （ π ， 3 π 2 ）

  D． （ 3 π 2 ， 2 π ）
  組卷：317引用：1難度：0.8

  解析

• 7．已知△ABC是面積為

  3

  的等邊三角形，且其頂點都在球O的表面上，若球心O到面ABC的距離為1，則球O的表面積為（　　）

  A．20π

  B． 28 3 π

  C．16π

  D． 16 3 π
  組卷：280引用：1難度：0.8

  解析

• 8．設(shè)集合

  A

  =

  {

  x

  |

  x

  +

  1

  x

  -

  4

  ≤

  0

  }

  ，B={x|-1＜x＜3}，則A∩（?_RB）=（　　）

  A．{x|3≤x≤4或x=-1}	B．{x|3≤x≤4}
  C．{x|3≤x＜4或x=-1}	D．{x|3≤x＜4}
  組卷：133引用：2難度：0.8

  解析
• 9．系統(tǒng)找不到該試題

二、填空題（本大題共6小題，共30.0分）

• 10．已知復數(shù)

  z

  =

  1

  -

  2

  i

  i

  （i是虛數(shù)單位），則z的虛部是

  ．
  組卷：35引用：1難度：0.8

  解析

• 11．

  1

  x

  3

  ?

  （

  x

  +

  2

  x

  ）

  6

  的展開式中常數(shù)項為

  ．
  組卷：314引用：4難度：0.7

  解析

• 12．正實數(shù)x,y滿足

  1

  x

  +

  4

  y

  =

  2

  ，且不等式

  x

  +

  y

  4

  ≥

  m

  2

  -

  m

  恒成立，則實數(shù)m的取值范圍為

  ．
  組卷：643引用：11難度：0.6

  解析

• 13．已知函數(shù)

  f

  （

  x

  ）

  =

  2

  ef

  ′

  （

  e

  ）

  lnx

  -

  x

  e

  ，則函數(shù)f（x）的最大值為

  ．
  組卷：15引用：2難度：0.6

  解析

• 14．甲乙兩人各射擊一次．擊中目標的概率分別為

  2

  3

  和

  3

  4

  ．假設(shè)兩人射擊是否擊中目標相互之間沒有影響，每次射擊是否擊中目標相互之間也沒有影響，求兩人各射擊2次．甲恰好擊中目標2次且乙恰好擊中目標一次的概率為

  ．
  組卷：112引用：3難度：0.7

  解析

• 15．在數(shù)列a_n中，a₁=a,a₂=b,且a_n=|a_n-1|-a_n-2，n=3，4，5，…．
  給出下列命題：
  ①?a,b∈R，使得a₁，a₂，a₃均為負數(shù)；
  ②?a,b∈R，使得a₁，a₂，a₃均為正數(shù)；
  ③若a=5，b=1，則a₈₈=-3．
  其中真命題的序號為

  ．（填出所有真命題的序號）
  組卷：7引用：4難度：0.7

  解析

三、解答題（本大題共5小題，共75分.解答應(yīng)寫出文字說明，證明過程或演算步驟）

• 16．已知函數(shù)

  f

  （

  x

  ）

  =

  ln

  （

  2

  x

  +

  a

  ）

  （

  a

  ∈

  R

  ）

  ．
  （1）若函數(shù)F（x）=f（x）-ln[（2-a）x+3a-3]有唯一零點，求實數(shù)a的取值范圍；
  （2）若對任意實數(shù)

  m

  ∈

  [

  3

  4

  ，

  1

  ]

  ，對任意x₁，x₂∈[m,4m-1]，恒有|f（x₁）-f（x₂）|≤ln2成立，求正實數(shù)a的取值范圍．
  組卷：218引用：5難度：0.3

  解析

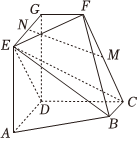• 17．如圖，AD∥BC且AD=2BC，AD⊥CD，EG∥AD且EG=AD，CD∥FG且CD=2FG，DG⊥平面ABCD，DA=DC=DG=2．
  （1）若M為CF的中點，N為EG的中點，求證：MN∥平面CDE；
  （2）求二面角E-BC-F的正弦值；
  （3）若點P在線段DG上，且直線BP與平面ADGE所成的角為60°，求點P到平面CDE的距離．
  組卷：60引用：6難度：0.5

  解析

• 18．在△ABC中，a=3，

  b

  =

  7

  ，c=2，求∠B，S_△ABC．
  組卷：4引用：1難度：0.7

  解析

• 19．在△ABC中，a=3，

  b

  =

  7

  ，c=2，求∠B，S_△ABC．
  組卷：8引用：1難度：0.8

  解析

• 20．已知數(shù)列{a_n}為等差數(shù)列，a₁=1，公差d＞0，數(shù)列{b_n}為等比數(shù)列，且a₂=b₂，a₈=b₄，a₃₂=b₆（n∈N^*）．
  （1）求數(shù)列{b_n}的公比q；
  （2）設(shè)

  c

  n

  =

  a

  n

  ?

  b

  2

  n

  ，數(shù)列{c_n}的前n項和為T_n，求滿足

  T

  n

  ＞

  4

  a

  n

  +

  1

  的n的最小值．
  組卷：20引用：2難度：0.5

  解析