當前位置：試卷中心 > 試卷詳情

2022年湖南省高考數學調研試卷（3月份）

發布：2025/6/29 10:0:14

一、單選題（本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

1．據研究，人的智力高低可以用智商（IQ）來衡量，且IQ～N（100，15²），若定義IQ∈[0，70）稱為智商低下，IQ∈[70，85）稱為智商中下，IQ∈[85，115）稱為智商正常，IQ∈[115，130）稱為智商優秀，IQ∈[130，+∞）稱為智商超常，則一般人群中智商優秀所占的比例約為（　　）（參考數據：若X～N（μ，σ²），則P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤μ+3σ）≈0.9973．）
A．13.59% B．15.65% C．27.18% D．29.14%
組卷：131引用：2難度：0.8
解析
2．若雙曲線C₁：y²-3x²=λ（λ≠0）的右焦點與拋物線C₂；y²=8x的焦點重合，則實數λ=（　　）
A．±3 B．-
3
C．3 D．-3
組卷：146引用：4難度：0.6
解析
3．
（
x
+
1
x
）
9
展開式中的第四項是（　　）
A．56x³ B．84x³ C．56x⁴ D．84x⁴
組卷：66引用：4難度：0.9
解析
4．如圖1所示，宮燈又稱宮廷花燈，是中國彩燈中富有特色的漢民族傳統手工藝品之一．圖2是小明為自家設計的一個花燈的直觀圖，該花燈由上面的正六棱臺與下面的正六棱柱組成，若正六棱臺的上、下兩個底面的邊長分別為4dm和2dm,正六棱臺與正六棱柱的高分別為1dm和6dm,則該花燈的表面積為（　　）
?
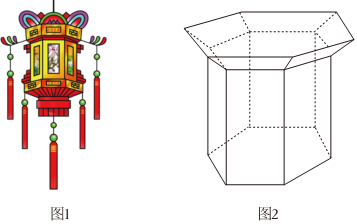A．
（
108
+
30
3
）
d
m
2
B．
（
72
+
30
3
）
d
m
2
C．
（
64
+
24
3
）
d
m
2
D．
（
48
+
24
3
）
d
m
2
組卷：90引用：1難度：0.7
解析
5．已知集合U={-1，0，1，2，3}，集合P={0，1，2}，集合Q={-1，0}，則（?_UP）∪Q=（　　）
A．{3} B．{-1} C．{-1，1，2，3} D．{-1，0，3}
組卷：122引用：4難度：0.9
解析
6．已知函數f（x）=nx+lnx（n∈N^*）的圖象在點
（
1
n
，
f
（
1
n
）
）
處的切線的斜率為a_n，則數列
{
1
a
n
a
n
+
1
}
的前n項和S_n為（　　）
A．
1
n
+
1
B．
3
n
2
+
5
n
2
（
n
+
1
）
（
n
+
2
）
C．
n
4
（
n
+
1
）
D．
3
n
2
+
5
n
8
（
n
+
1
）
（
n
+
2
）
組卷：170引用：7難度：0.7
解析
7．若冪函數f（x）的圖象經過點
（
9
，
1
3
）
，則f（2）=（　　）
A．
2
2
B．
2
C．
1
4
D．4
組卷：13引用：2難度：0.7
解析
8．已知i為虛數單位，且復數a²-1+（a-1）i是純虛數，則實數a的值為（　　）
A．1或-1 B．1 C．-1 D．0
組卷：362引用：4難度：0.9
解析

二、多選題（本大題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求，全部選對的得5分，部分選對的得2分，有選錯的得0分。）

9．將函數
f
（
x
）
=
cos
（
ωx
-
π
3
）
（
ω
＞
0
）
的圖象向右平移
π
6
個單位長度后，得到函數g（x）的圖象，若g（x）為奇函數，則ω的取值可以為（　　）
A．1 B．6 C．7 D．8
組卷：30引用：3難度：0.7
解析

10．已知函數
f
（
x
）
=
3
sinωx
+
cosωx
（
ω
＞
0
）
，下列說法中正確的有（　　）

A．若ω=1，則f（x）在

（

，

）

上是單調增函數

B．若

（

）

（

）

，則正整數ω的最小值為2

C．若ω=2，則把函數y=f（x）的圖象向右平移

個單位長度，所得到的圖象關于原點對稱

D．若f（x）在（0，π）上有且僅有3個零點，則

＜

≤

組卷：115引用：4難度：0.6

解析

11．圓C：x²+y²+4x-6y-3=0，直線l：3x-4y-7=0，點P在圓C上，點Q在直線l上，則下列結論正確的是（　　）

A．直線l與圓C相交

B．|PQ|的最小值是1

C．從Q點向圓C引切線，切線長的最小值是3

D．直線y=k（x-2）+4與曲線y=1+

有兩個不同的交點，則實數k的取值范圍是

（

，

]

組卷：244引用：8難度：0.5

解析

12．下列說法正確的是（　　）

A．用簡單隨機抽樣的方法從含有50個個體的總體中抽取一個容量為5的樣本，則個體m被抽到的概率是0.1

B．已知一組數據1，2，3，3，4，5的眾數大于中位數

C．數據27，12，14，30，15，17，19，23的第70百分位數是21

D．甲乙丙三種個體按3：1：2的比例分層抽樣，如果抽取的甲個體數為9，則樣本容量為18

組卷：224引用：5難度：0.8

解析

三、填空題（本大題共4小題，每小題5分，共20分。）

13．已知平面α的一個法向量為（3λ，6，λ+6），平面β的一個法向量為（λ+1，3，2λ），若α∥β，則λ=
．
組卷：55引用：4難度：0.9
解析
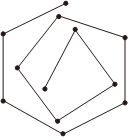14．如圖，畫一個正三角形，不畫第三邊；接著畫正方形，對這個正方形，不畫第四邊，接著畫正五邊形；對這個正五邊形不畫第五邊，接著畫正六邊形；……，這樣無限畫下去，形成一條無窮伸展的等邊折線．設第n條線段與第n+1條線段所夾的角為
θ
n
（
n
∈
N
*
，
θ
n
∈
（
0
，
π
）
）
，則θ₂₀₂₂=
．
組卷：88引用：3難度：0.6
解析
15．函數
f
（
x
）
=
|
x
-
2
|
-
|
x
+
2
|
的值域為
．
組卷：311引用：1難度：0.8
解析
16．過拋物線y²=px（p＞0）的焦點F作傾斜角為45°的直線交拋物線于A，B兩點，若線段AB的長為8，則p=

．
組卷：23引用：2難度：0.5
解析

四、解答題：（本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。）

17．已知數列{a_n}的前n項和為S_n，且S_n=2a_n-n.
（Ⅰ）證明數列{a_n+1}是等比數列，求數列{a_n}的通項公式；
（Ⅱ）記b_n=
1
a
n
+
1
+
1
a
n
a
n
+
1
，求數列{b_n}的前n項和T_n．
組卷：145引用：3難度：0.5
解析
18．已知函數f（x）=xcosx,g（x）=asinx.
（1）若a=1，證明：當x∈（0，π）時，x＞g（x）＞f（x）；
（2）當x∈（-π，0）∪（0，π）時，
f
（
x
）
g
（
x
）
＜
sinx
x
，求a的取值范圍．
組卷：18引用：4難度：0.6
解析
19．在一次環保知識競賽中，有6道選擇題和2道判斷題放在一起供抽取，某支代表隊要抽3次，每次只抽一道題回答．
（Ⅰ）不放回的抽取試題，求恰好在第三次抽到判斷題的概率；
（Ⅱ）有放回的抽取試題，求在三次抽取中抽到判斷題的個數ξ的概率分布及ξ的期望．
組卷：19引用：2難度：0.3
解析
20．已知橢圓C：
x
2
4
+
y
2
3
=1的左、右頂點分別為A，B，右焦點為F，過點A且斜率為k（k≠0）的直線l交橢圓C于點P．
（1）若|AP|=
12
2
7
，求k的值；
（2）若圓F是以F為圓心，1為半徑的圓，連接PF，線段PF交圓F于點T，射線AP上存在一點Q，使得
QT
?
BT
為定值，證明：點Q在定直線上．
組卷：69引用：1難度：0.5
解析
21．在三角形ABC中，已知
tan
B
=
1
2
，
cos
C
=
-
10
10
．
（1）求角A的值；
（2）若△ABC的面積為
3
10
，求邊BC的長．
組卷：238引用：2難度：0.5
解析
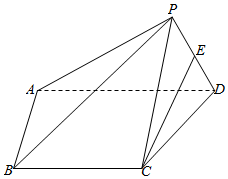22．如圖，已知四棱錐P-ABCD，AD∥BC且AB⊥AD，
AD
=
6
2
，AB=4，
BC
=
4
2
，△PAD的面積等于
12
2
，E是PD是中點．
（Ⅰ）求四棱錐P-ABCD體積的最大值；
（Ⅱ）若
PB
=
4
5
，
tan
∠
PAD
=
2
2
．
（ⅰ）求證：AD⊥PC；
（ⅱ）求直線CE與平面PBC所成角的正弦值．
組卷：445引用：2難度：0.3
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ 108 + 30 3 ） d m 2	B．（ 72 + 30 3 ） d m 2
C．（ 64 + 24 3 ） d m 2	D．（ 48 + 24 3 ） d m 2

A． 1 n + 1	B． 3 n 2 + 5 n 2 （ n + 1 ）（ n + 2 ）
C． n 4 （ n + 1 ）	D． 3 n 2 + 5 n 8 （ n + 1 ）（ n + 2 ）

2022年湖南省高考數學調研試卷（3月份）

一、單選題（本大題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。）

2．若雙曲線C1：y2-3x2=λ（λ≠0）的右焦點與拋物線C2；y2=8x的焦點重合，則實數λ=（ ）

3．（x+1x）9展開式中的第四項是（ ）

5．已知集合U={-1，0，1，2，3}，集合P={0，1，2}，集合Q={-1，0}，則（?UP）∪Q=（ ）

6．已知函數f（x）=nx+lnx（n∈N*）的圖象在點（1n，f（1n））處的切線的斜率為an，則數列{1anan+1}的前n項和Sn為（ ）

7．若冪函數f（x）的圖象經過點（9，13），則f（2）=（ ）

8．已知i為虛數單位，且復數a2-1+（a-1）i是純虛數，則實數a的值為（ ）

二、多選題（本大題共4小題，每小題5分，共20分。在每小題給出的選項中，有多項符合題目要求，全部選對的得5分，部分選對的得2分，有選錯的得0分。）

9．將函數f（x）=cos（ωx-π3）（ω＞0）的圖象向右平移π6個單位長度后，得到函數g（x）的圖象，若g（x）為奇函數，則ω的取值可以為（ ）

10．已知函數f（x）=3sinωx+cosωx（ω＞0），下列說法中正確的有（ ）

11．圓C：x2+y2+4x-6y-3=0，直線l：3x-4y-7=0，點P在圓C上，點Q在直線l上，則下列結論正確的是（ ）

12．下列說法正確的是（ ）

三、填空題（本大題共4小題，每小題5分，共20分。）

13．已知平面α的一個法向量為（3λ，6，λ+6），平面β的一個法向量為（λ+1，3，2λ），若α∥β，則λ=．

15．函數f（x）=|x-2|-|x+2|的值域為 ．

16．過拋物線y2=px（p＞0）的焦點F作傾斜角為45°的直線交拋物線于A，B兩點，若線段AB的長為8，則p= ．

四、解答題：（本大題共6小題，共70分。解答應寫出文字說明、證明過程或演算步驟。）

17．已知數列{an}的前n項和為Sn，且Sn=2an-n.（Ⅰ）證明數列{an+1}是等比數列，求數列{an}的通項公式；（Ⅱ）記bn=1an+1+1anan+1，求數列{bn}的前n項和Tn．

18．已知函數f（x）=xcosx,g（x）=asinx.（1）若a=1，證明：當x∈（0，π）時，x＞g（x）＞f（x）；（2）當x∈（-π，0）∪（0，π）時，f（x）g（x）＜sinxx，求a的取值范圍．

21．在三角形ABC中，已知tanB=12，cosC=-1010．（1）求角A的值；（2）若△ABC的面積為310，求邊BC的長．

22．如圖，已知四棱錐P-ABCD，AD∥BC且AB⊥AD，AD=62，AB=4，BC=42，△PAD的面積等于122，E是PD是中點．（Ⅰ）求四棱錐P-ABCD體積的最大值；（Ⅱ）若PB=45，tan∠PAD=22．（ⅰ）求證：AD⊥PC；（ⅱ）求直線CE與平面PBC所成角的正弦值．

2．若雙曲線C₁：y²-3x²=λ（λ≠0）的右焦點與拋物線C₂；y²=8x的焦點重合，則實數λ=（　　）

3．
（
x
+
1
x
）
9
展開式中的第四項是（　　）

5．已知集合U={-1，0，1，2，3}，集合P={0，1，2}，集合Q={-1，0}，則（?_UP）∪Q=（　　）

6．已知函數f（x）=nx+lnx（n∈N^*）的圖象在點
（
1
n
，
f
（
1
n
）
）
處的切線的斜率為a_n，則數列
{
1
a
n
a
n
+
1
}
的前n項和S_n為（　　）

7．若冪函數f（x）的圖象經過點
（
9
，
1
3
）
，則f（2）=（　　）

8．已知i為虛數單位，且復數a²-1+（a-1）i是純虛數，則實數a的值為（　　）

9．將函數
f
（
x
）
=
cos
（
ωx
-
π
3
）
（
ω
＞
0
）
的圖象向右平移
π
6
個單位長度后，得到函數g（x）的圖象，若g（x）為奇函數，則ω的取值可以為（　　）

10．已知函數
f
（
x
）
=
3
sinωx
+
cosωx
（
ω
＞
0
）
，下列說法中正確的有（　　）

11．圓C：x²+y²+4x-6y-3=0，直線l：3x-4y-7=0，點P在圓C上，點Q在直線l上，則下列結論正確的是（　　）

12．下列說法正確的是（　　）

13．已知平面α的一個法向量為（3λ，6，λ+6），平面β的一個法向量為（λ+1，3，2λ），若α∥β，則λ=
．

15．函數
f
（
x
）
=
|
x
-
2
|
-
|
x
+
2
|
的值域為
．

16．過拋物線y²=px（p＞0）的焦點F作傾斜角為45°的直線交拋物線于A，B兩點，若線段AB的長為8，則p=

．

17．已知數列{a_n}的前n項和為S_n，且S_n=2a_n-n.
（Ⅰ）證明數列{a_n+1}是等比數列，求數列{a_n}的通項公式；
（Ⅱ）記b_n=
1
a
n
+
1
+
1
a
n
a
n
+
1
，求數列{b_n}的前n項和T_n．

18．已知函數f（x）=xcosx,g（x）=asinx.
（1）若a=1，證明：當x∈（0，π）時，x＞g（x）＞f（x）；
（2）當x∈（-π，0）∪（0，π）時，
f
（
x
）
g
（
x
）
＜
sinx
x
，求a的取值范圍．

21．在三角形ABC中，已知
tan
B
=
1
2
，
cos
C
=
-
10
10
．
（1）求角A的值；
（2）若△ABC的面積為
3
10
，求邊BC的長．