當前位置：試卷中心 > 試卷詳情

2024年河南省信陽市羅山縣三校聯考高考數學二模試卷

發布：2025/6/29 12:0:14

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是正確的．請把正確的選項填涂在答題卡相應的位置上．

1．若α∈（0，
π
2
），tan2α=
cosα
2
-
sinα
，則tanα=（　　）
A．
15
15
B．
5
5
C．
5
3
D．
15
3
組卷：701引用：19難度：0.7
解析
2．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右焦點為F，若過點F且傾斜角為60°的直線與雙曲線的右支有且只有一個交點，則此雙曲線離心率的取值范圍是（　　）
A．（1，2] B．
（
1
，
3
]
C．（2，+∞） D．[2，+∞）
組卷：450引用：2難度：0.7
解析
3．已知角α的終邊過點P（-6，8），則cosα的值是（　　）
A．
-
3
5
B．
3
5
C．
-
4
5
D．
4
5
組卷：73引用：2難度：0.9
解析
4．已知函數
f
（
x
）
=
3
x
，

x
≤
0
lo
g
2
x

，
x
＞
0
，則
f
（
f
（
1
2
）
）
的值是（　　）
A．-1 B．3 C．
1
3
D．
3
組卷：2746引用：17難度：0.9
解析
5．如圖，圓臺的高為4，上、下底面半徑分別為3，5，O₁，O₂分別為下底面圓和上底面圓的圓心，M，N分別在上、下底面圓的圓周上，且
?
O
2
M
，
O
1
N
?
=
120
°
，則
|
MN
|
=（　　）
A．
65
B．
5
2
C．
35
D．5
組卷：24引用：1難度：0.5
解析
6．已知集合A={1，2，3}，B={3，4}，則A∩B=（　　）
A．{1，2，3} B．{1，3} C．{3} D．?
組卷：2引用：1難度：0.8
解析
7．圓x²+y²-4x-4y-10=0上的點到直線x+y-14=0的最大距離與最小距離的差是（　　）
A．30 B．18 C．6
2
D．5
2
組卷：297引用：4難度：0.7
解析
8．在等差數列{a_n}中，a₁+a₂=1，a₃+a₄=5，則a₂₀₂₂+a₂₀₂₃=（　　）
A．2022 B．2023 C．4043 D．4044
組卷：171引用：2難度：0.7
解析

二、選擇題：本題共3小題，每小題5分，共15分．在每小題給出的選項中，有多項符合題目要．全部選對的得5分，部分選對的得2分，有選錯的得0分．

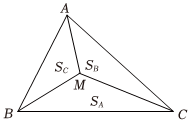9．“奔馳定理”因其幾何表示酷似奔馳的標志得來，是平面向量中一個非常優美的結論．奔馳定理與三角形四心（重心、內心、外心、垂心）有著神秘的關聯．它的具體內容是：已知M是△ABC內一點，△BMC，△AMC，△AMB的面積分別為S_A，S_B，S_C，且
S
A
?
MA
+
S
B
?
MB
+
S
c
?
MC
=
0
．以下命題正確的有（　　）

A．若S_A：S_B：S_C=1：1：1，則M為△ABC的重心

B．若M為△ABC的內心，則

C．若∠BAC=45°，∠ABC=60°，M為△ABC的外心，則

：

D．若M為△ABC的垂心，

，則

cos

∠

AMB

組卷：948引用：20難度：0.5

解析

10．已知曲線C上的點P（x,y）滿足方程x|x-1|+y|y-1|=0，則下列結論中正確的是（　　）

A．當x∈[-1，2]時，曲線C的長度為

B．當x∈[-1，2]時，

的最大值為1，最小值為-

C．曲線C與x軸、y軸所圍成的封閉圖形的面積和為

D．若平行于x軸的直線與曲線C交于A，B，M三個不同的點，其橫坐標分別為x₁，x₂，x₃，則x₁+x₂+x₃的取值范圍是（2，

）

組卷：61引用：6難度：0.5

解析

11．已知向量
a
=
（
1
，
1
，-
1
）
，
b
=
（
2
，-
1
，
0
）
，
c
=
（
0
，
1
，-
2
）
，則下列結論正確的是（　　）
A．
a
?
（
b
+
c
）
=
4
B．
（
a
-
b
）
?
（
b
-
c
）
=
-
8
C．記
a
與
b
-
c
的夾角為θ，則
cosθ
=
1
3
D．若
（
a
+
λ
b
）
⊥
c
，則λ=3
組卷：82引用：3難度：0.7
解析

三、填空題：本題共3小題，每小題5分，共15分．

12．已知圓的方程是（x-1）²+（y-1）²=1，則過點A（2，4）與圓相切的直線方程是
．
組卷：36引用：3難度：0.5
解析
13．對于任意實數x,不等式|x+1|+|x-2|≥a²-2a恒成立，則實數a的取值范圍是
．
組卷：14引用：1難度：0.5
解析
14．已知橢圓
E
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左，右焦點分別為F₁，F₂，過F₂的直線與E交于點A，B，直線l為E在點A處的切線，點B關于l的對稱點為M．由橢圓的光學性質知，F₁，A，M三點共線．若|AB|=a,
|
B
F
1
|
|
M
F
1
|
=
5
7
，則
|
B
F
2
|
|
A
F
1
|
=
．
組卷：79引用：1難度：0.7
解析

四、解答題：本題共5小題，共80分，解答應寫出文字說明、證明過程或演算步驟．

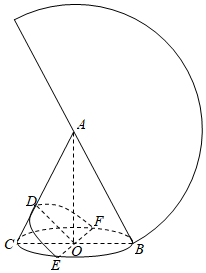15．如圖，圓錐的展開側面圖是一個半圓，BC、EF是底面圓O的兩條互相垂直的直徑，D為母線AC的中點，已知過EF與D的平面與圓錐側面的交線是以D為頂點、DO為對稱軸的拋物線的一部分．
（1）證明：圓錐的母線與底面所成的角為
π
3
；
（2）若圓錐的側面積為8π，求拋物線焦點到準線的距離．
組卷：51引用：1難度：0.6
解析

16．第17屆亞運會將于2014年9月18日至10月4日在韓國仁川進行，為了搞好接待工作，組委會招募了16名男志愿者和14名女志愿者，調查發現，男、女志愿者中分別有10人和6人喜愛運動，其余不喜愛．
（1）根據調查數據制作2×2列聯表；
（2）根據列聯表的獨立性檢驗，能否認為性別與喜愛運動有關？

參考數據當Χ²≤2.706時，無充分證據判定變量A，B有關聯，可以認為兩變量無關聯；

當Χ²＞2.706時，有90%把握判定變量A，B有關聯；

當Χ²＞3.841時，有95%把握判定變量A，B有關聯；

當Χ²＞6.635時，有99%把握判定變量A，B有關聯．

（參考公式：
Χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，其中n=a+b+c+d.）

組卷：10引用：3難度：0.5

解析

17．已知等差數列{a_n}的前n項和為S_n，a₃=3，S₄=10，求數列{
1
S
n
}的前n項和T_n．
組卷：31引用：1難度：0.8
解析
18．關于函數f（x）=
a
x
+lnx.
①x=2是f（x）的極小值點；②f（x）在（1，a）處的切線垂直于直線x-y=0．
（1）從條件①，②中選一個，求a的值；
（2）在（1）的結果下，若對任意兩個正實數x₁，x₂，且x₁≠x₂，有f（x₁）=f（x₂），求證：x₁+x₂＞2a.
組卷：35引用：1難度：0.5
解析
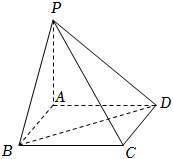19．如圖，在四棱錐P-ABCD中，底面ABCD是邊長為1的正方形，PA⊥底面ABCD，PA=AB．
（1）證明：平面PBD⊥平面PAC；
（2）點M在平面PBD內，直線AM⊥平面PBD，求四棱錐M-ABCD的體積．
組卷：137引用：2難度：0.6
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

參考數據	當Χ²≤2.706時，無充分證據判定變量A，B有關聯，可以認為兩變量無關聯；
	當Χ²＞2.706時，有90%把握判定變量A，B有關聯；
	當Χ²＞3.841時，有95%把握判定變量A，B有關聯；
	當Χ²＞6.635時，有99%把握判定變量A，B有關聯．

2024年河南省信陽市羅山縣三校聯考高考數學二模試卷

一、選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是正確的．請把正確的選項填涂在答題卡相應的位置上．

1．若α∈（0，π2），tan2α=cosα2-sinα，則tanα=（ ）

2．已知雙曲線x2a2-y2b2=1（a＞0，b＞0）的右焦點為F，若過點F且傾斜角為60°的直線與雙曲線的右支有且只有一個交點，則此雙曲線離心率的取值范圍是（ ）

3．已知角α的終邊過點P（-6，8），則cosα的值是（ ）

4．已知函數f（x）=3x， x≤0log2x ，x＞0，則f（f（12））的值是（ ）

5．如圖，圓臺的高為4，上、下底面半徑分別為3，5，O1，O2分別為下底面圓和上底面圓的圓心，M，N分別在上、下底面圓的圓周上，且?O2M，O1N?=120°，則|MN|=（ ）

6．已知集合A={1，2，3}，B={3，4}，則A∩B=（ ）

7．圓x2+y2-4x-4y-10=0上的點到直線x+y-14=0的最大距離與最小距離的差是（ ）

8．在等差數列{an}中，a1+a2=1，a3+a4=5，則a2022+a2023=（ ）

二、選擇題：本題共3小題，每小題5分，共15分．在每小題給出的選項中，有多項符合題目要．全部選對的得5分，部分選對的得2分，有選錯的得0分．

10．已知曲線C上的點P（x,y）滿足方程x|x-1|+y|y-1|=0，則下列結論中正確的是（ ）

11．已知向量a=（1，1，-1），b=（2，-1，0），c=（0，1，-2），則下列結論正確的是（ ）

三、填空題：本題共3小題，每小題5分，共15分．

12．已知圓的方程是（x-1）2+（y-1）2=1，則過點A（2，4）與圓相切的直線方程是．

13．對于任意實數x,不等式|x+1|+|x-2|≥a2-2a恒成立，則實數a的取值范圍是 ．

14．已知橢圓E：x2a2+y2b2=1（a＞b＞0）的左，右焦點分別為F1，F2，過F2的直線與E交于點A，B，直線l為E在點A處的切線，點B關于l的對稱點為M．由橢圓的光學性質知，F1，A，M三點共線．若|AB|=a,|BF1||MF1|=57，則|BF2||AF1|=．

四、解答題：本題共5小題，共80分，解答應寫出文字說明、證明過程或演算步驟．

17．已知等差數列{an}的前n項和為Sn，a3=3，S4=10，求數列{1Sn}的前n項和Tn．

19．如圖，在四棱錐P-ABCD中，底面ABCD是邊長為1的正方形，PA⊥底面ABCD，PA=AB．（1）證明：平面PBD⊥平面PAC；（2）點M在平面PBD內，直線AM⊥平面PBD，求四棱錐M-ABCD的體積．

1．若α∈（0，
π
2
），tan2α=
cosα
2
-
sinα
，則tanα=（　　）

2．已知雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右焦點為F，若過點F且傾斜角為60°的直線與雙曲線的右支有且只有一個交點，則此雙曲線離心率的取值范圍是（　　）

3．已知角α的終邊過點P（-6，8），則cosα的值是（　　）

4．已知函數
f
（
x
）
=
3
x
，

x
≤
0
lo
g
2
x

，
x
＞
0
，則
f
（
f
（
1
2
）
）
的值是（　　）

5．如圖，圓臺的高為4，上、下底面半徑分別為3，5，O₁，O₂分別為下底面圓和上底面圓的圓心，M，N分別在上、下底面圓的圓周上，且
?
O
2
M
，
O
1
N
?
=
120
°
，則
|
MN
|
=（　　）

6．已知集合A={1，2，3}，B={3，4}，則A∩B=（　　）

7．圓x²+y²-4x-4y-10=0上的點到直線x+y-14=0的最大距離與最小距離的差是（　　）

8．在等差數列{a_n}中，a₁+a₂=1，a₃+a₄=5，則a₂₀₂₂+a₂₀₂₃=（　　）

10．已知曲線C上的點P（x,y）滿足方程x|x-1|+y|y-1|=0，則下列結論中正確的是（　　）

11．已知向量
a
=
（
1
，
1
，-
1
）
，
b
=
（
2
，-
1
，
0
）
，
c
=
（
0
，
1
，-
2
）
，則下列結論正確的是（　　）

12．已知圓的方程是（x-1）²+（y-1）²=1，則過點A（2，4）與圓相切的直線方程是
．

13．對于任意實數x,不等式|x+1|+|x-2|≥a²-2a恒成立，則實數a的取值范圍是
．

17．已知等差數列{a_n}的前n項和為S_n，a₃=3，S₄=10，求數列{
1
S
n
}的前n項和T_n．

19．如圖，在四棱錐P-ABCD中，底面ABCD是邊長為1的正方形，PA⊥底面ABCD，PA=AB．
（1）證明：平面PBD⊥平面PAC；
（2）點M在平面PBD內，直線AM⊥平面PBD，求四棱錐M-ABCD的體積．