當前位置：試卷中心 > 試卷詳情

2025年廣東省高考數學試卷（新高考Ⅰ）

發布：2025/6/29 12:0:14

一、選擇題：本大題共8小題，每小題5分，共計40分。每小題給出的四個選項中，只有一個選項是正確的。請把正確的選項填涂在答題卡相應的位置上。

1．在平面直角坐標系中，O為坐標原點，已知圓O的半徑為3，直線l₁，l₂互相垂直，垂足為M（1，
5
），且l₁與圓O相交于A，C兩點，l₂與圓O相交于B，D兩點，則四邊形ABCD的面積的最大值為（　　）
A．10 B．12 C．13 D．15
組卷：169引用：5難度：0.5
解析
2．下列各物理量表示向量的是（　　）
A．質量 B．距離 C．力 D．體重
組卷：34引用：1難度：0.7
解析
3．王老師在課堂中與學生探究某雙曲線的性質時，有四位同學分別給出了一個結論：
甲：該雙曲線的實軸長是
4
3
；
乙：該雙曲線的虛軸長是2；
丙：該雙曲線的焦距為8；
丁：該雙曲線的離心率為
2
3
3
．
如果只有一位同學的結論是錯誤的，那么這位同學是（　　）
A．甲 B．乙 C．丙 D．丁
組卷：70引用：3難度：0.7
解析
4．已知集合A={0，2}，集合B={-2，-1，0}，則A∩B=（　　）
A．{0} B．{0，2} C．{-2，-1，0} D．{-2，-1，0，2}
組卷：27引用：1難度：0.9
解析
5．與函數
y
=
tan
（
2
x
+
π
4
）
的圖象不相交的一條直線是（　　）
A．
x
=
π
2
B．
y
=
π
2
C．
x
=
π
8
D．
y
=
π
8
組卷：458引用：10難度：0.8
解析
6．已知全集U={x∈N||x-3|≤3}，集合A={2，4}，則?_UA=（　　）
A．{2，4} B．{1，3，5，6}
C．{0，1，2，3，5，6} D．{0，1，3，5，6}．
組卷：47引用：2難度：0.7
解析
7．設
a
=
3
1
15
，
b
=
1
5
1
3
，c=log₁₅
1
3
，則a,b,c的大小關系是（　　）
A．a＜b＜c B．a＜c＜b C．c＜a＜b D．c＜b＜a
組卷：106引用：2難度：0.8
解析
8．復數
z
=
5
+
5
i
1
-
3
i
的實部與虛部之和為（　　）
A．1 B．-1 C．3 D．-3
組卷：375引用：3難度：0.8
解析

二、選擇題：本題共3小題，每小題6分，共18分。在每小題給出的選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。

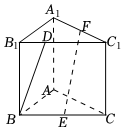9．如圖，在直三棱柱ABC-A₁B₁C₁中，∠BAC=90°，AB=AC=AA₁=2，E，F分別是BC，A₁C₁的中點，D在線段B₁C₁上，則下列說法中正確的有（　　）
A．EF∥平面AA₁B₁B
B．若D是B₁C₁的中點，則BD⊥EF
C．若
EF
在平面ABC上的投影向量為
EH
，則
EH
?
BC
=
2
D．當cos＜
BD
，
EF
＞=
3
10
10
時，線段BD的長為
3
2
2
組卷：153引用：1難度：0.5
解析

10．已知拋物線C：y²=4x的焦點為F，過點F的直線交C于兩點M（x₁，y₁），N（x₂，y₂），點M在準線l上的射影為A，則（　　）

A．若x₁+x₂=6，則|MN|=8

B．若點P的坐標為（2，1），則|MP|+|MF|的最小值為4

C．

D．若直線過點（0，1）且與拋物線C有且僅有一個公共點，則滿足條件的直線有2條

組卷：159引用：6難度：0.5

解析

11．在△ABC中，角A，B，C所對的邊分別為a,b,c,下列說法中正確的是（　　）
A．若A＞B，則sinA＞sinB
B．若
a
cos
B
=
b
cos
A
，則△ABC為一定是等腰三角形
C．
a
sin
A
=
b
+
c
sin
B
+
sin
C
D．若△ABC為銳角三角形，則sinA＞cosB
組卷：48引用：2難度：0.6
解析

三、填空題：本大題共3小題，每小題5分，共計15分。

12．已知{a_n}是無窮等比數列，若{a_n}的每一項都等于它后面所有項的k倍，則實數k的取值范圍是
．
組卷：99引用：2難度：0.5
解析
13．已知f（x）=x²+2xf'（1），則f（x）在x=-
1
2
的切線方程為

．
組卷：29引用：1難度：0.7
解析
14．已知離散型隨機變量ξ的分布如表：若隨機變量ξ的期望值
E
（
ξ
）
=
1
2
，則D（2ξ+1）=
．

ξ -2 0 2

P a b
1
2

組卷：182引用：1難度：0.6
解析

四、解答題：本題共5小題，共77分。解答應寫出文字說明、證明過程或演算步驟。

15．已知函數
f
（
x
）
=
ln
（
2
x
+
a
）
（
a
∈
R
）
．
（1）若函數F（x）=f（x）-ln[（2-a）x+3a-3]有唯一零點，求實數a的取值范圍；
（2）若對任意實數
m
∈
[
3
4
，
1
]
，對任意x₁，x₂∈[m,4m-1]，恒有|f（x₁）-f（x₂）|≤ln2成立，求正實數a的取值范圍．
組卷：218引用：5難度：0.3
解析
16．已知正項等差數列{a_n}的前n項和為S_n，且
21
∑
i
=
1
1
a
i
a
i
+
1
=
7
10
，a_n+2-a_n=
2
3
．
（1）求S_n；
（2）若b_n=（9a_n-29）?2^n-1，求數列{b_n}的前n項和T_n．
組卷：145引用：2難度：0.4
解析
17．已知橢圓E：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）的長軸長是短軸長的兩倍，且過點（-
3
，
1
2
）．
（Ⅰ）求橢圓E的方程；
（Ⅱ）設橢圓E的下頂點為點A．若不過點A且不垂直于坐標軸的直線l交橢圓E于P，Q兩點，直線AP，AQ分別與x軸交于M，N兩點．若M，N的橫坐標之積是2，證明：直線l過定點．
組卷：95引用：5難度：0.3
解析
18．如圖，三棱柱ABC-A₁B₁C₁中，側面BB₁C₁C為菱形，B₁C的中點為O，AC=AB₁．

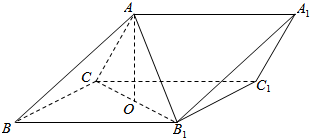
（1）文字敘述平面與平面垂直判定定理；
（2）求證：平面ABO⊥平面ACB₁．
組卷：29引用：1難度：0.3
解析

19．為進一步保護環境，加強治理空氣污染，某市環保監測部門對市區空氣質量進行調研，隨機抽查了市區100天的空氣質量等級與當天空氣中SO₂的濃度（單位：μg/m³），整理數據得到表：

SO₂的濃度
空氣質量等級 [0，50] （50，150] （150，475]

1（優） 28 6 2

2（良） 5 7 8

3（輕度污染） 3 8 9

4（中度污染） 1 12 11

若某天的空氣質量等級為1或2，則稱這天“空氣質量好”，若某天的空氣質量等級為3或4，則稱這天“空氣質量不好”，根據上述數據，回答以下問題．
（1）估計事件“該市一天的空氣質量好，且SO₂的濃度不超過150”的概率；
（2）完成下面的2×2列聯表．

SO₂的濃度合計

[0，150] （150，475]

空氣質量好 ___ _ _

空氣質量不好 _ _ _

合計 _ _ ___

（3）根據（2）中的列聯表，依據小概率值a=0.01的獨立性檢驗，能否據此推斷該市一天的空氣質量與當天SO₂的濃度有關？
附：
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，其中n=a+b+c+d.

a 0.05 0.025 0.010 0.001

x_a 3.841 5.024 6.635 10.828

組卷：15引用：1難度：0.8

解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

	SO₂的濃度		合計
	[0，150]	（150，475]	合計
空氣質量好	_____	_____	_____
空氣質量不好	_____	_____	_____
合計	_____	_____	_____

A．{2，4}	B．{1，3，5，6}
C．{0，1，2，3，5，6}	D．{0，1，3，5，6}．

SO₂的濃度空氣質量等級	[0，50]	（50，150]	（150，475]
1（優）	28	6	2
2（良）	5	7	8
3（輕度污染）	3	8	9
4（中度污染）	1	12	11

2025年廣東省高考數學試卷（新高考Ⅰ）

一、選擇題：本大題共8小題，每小題5分，共計40分。每小題給出的四個選項中，只有一個選項是正確的。請把正確的選項填涂在答題卡相應的位置上。

1．在平面直角坐標系中，O為坐標原點，已知圓O的半徑為3，直線l1，l2互相垂直，垂足為M（1，5），且l1與圓O相交于A，C兩點，l2與圓O相交于B，D兩點，則四邊形ABCD的面積的最大值為（ ）

2．下列各物理量表示向量的是（ ）

4．已知集合A={0，2}，集合B={-2，-1，0}，則A∩B=（ ）

5．與函數y=tan（2x+π4）的圖象不相交的一條直線是（ ）

6．已知全集U={x∈N||x-3|≤3}，集合A={2，4}，則?UA=（ ）

7．設a=3115，b=1513，c=log1513，則a,b,c的大小關系是（ ）

8．復數z=5+5i1-3i的實部與虛部之和為（ ）

二、選擇題：本題共3小題，每小題6分，共18分。在每小題給出的選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。

9．如圖，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AC=AA1=2，E，F分別是BC，A1C1的中點，D在線段B1C1上，則下列說法中正確的有（ ）

10．已知拋物線C：y2=4x的焦點為F，過點F的直線交C于兩點M（x1，y1），N（x2，y2），點M在準線l上的射影為A，則（ ）

11．在△ABC中，角A，B，C所對的邊分別為a,b,c,下列說法中正確的是（ ）

三、填空題：本大題共3小題，每小題5分，共計15分。

12．已知{an}是無窮等比數列，若{an}的每一項都等于它后面所有項的k倍，則實數k的取值范圍是．

13．已知f（x）=x2+2xf'（1），則f（x）在x=-12的切線方程為 ．

14．已知離散型隨機變量ξ的分布如表：若隨機變量ξ的期望值E（ξ）=12，則D（2ξ+1）=． ξ -2 0 2 P a b 12

四、解答題：本題共5小題，共77分。解答應寫出文字說明、證明過程或演算步驟。

15．已知函數f（x）=ln（2x+a）（a∈R）．（1）若函數F（x）=f（x）-ln[（2-a）x+3a-3]有唯一零點，求實數a的取值范圍；（2）若對任意實數m∈[34，1]，對任意x1，x2∈[m,4m-1]，恒有|f（x1）-f（x2）|≤ln2成立，求正實數a的取值范圍．

16．已知正項等差數列{an}的前n項和為Sn，且21∑i=11aiai+1=710，an+2-an=23．（1）求Sn；（2）若bn=（9an-29）?2n-1，求數列{bn}的前n項和Tn．

18．如圖，三棱柱ABC-A1B1C1中，側面BB1C1C為菱形，B1C的中點為O，AC=AB1．（1）文字敘述平面與平面垂直判定定理；（2）求證：平面ABO⊥平面ACB1．

1．在平面直角坐標系中，O為坐標原點，已知圓O的半徑為3，直線l₁，l₂互相垂直，垂足為M（1，
5
），且l₁與圓O相交于A，C兩點，l₂與圓O相交于B，D兩點，則四邊形ABCD的面積的最大值為（　　）

2．下列各物理量表示向量的是（　　）

4．已知集合A={0，2}，集合B={-2，-1，0}，則A∩B=（　　）

5．與函數
y
=
tan
（
2
x
+
π
4
）
的圖象不相交的一條直線是（　　）

6．已知全集U={x∈N||x-3|≤3}，集合A={2，4}，則?_UA=（　　）

7．設
a
=
3
1
15
，
b
=
1
5
1
3
，c=log₁₅
1
3
，則a,b,c的大小關系是（　　）

8．復數
z
=
5
+
5
i
1
-
3
i
的實部與虛部之和為（　　）

9．如圖，在直三棱柱ABC-A₁B₁C₁中，∠BAC=90°，AB=AC=AA₁=2，E，F分別是BC，A₁C₁的中點，D在線段B₁C₁上，則下列說法中正確的有（　　）

10．已知拋物線C：y²=4x的焦點為F，過點F的直線交C于兩點M（x₁，y₁），N（x₂，y₂），點M在準線l上的射影為A，則（　　）

11．在△ABC中，角A，B，C所對的邊分別為a,b,c,下列說法中正確的是（　　）

12．已知{a_n}是無窮等比數列，若{a_n}的每一項都等于它后面所有項的k倍，則實數k的取值范圍是
．

13．已知f（x）=x²+2xf'（1），則f（x）在x=-
1
2
的切線方程為

．

14．已知離散型隨機變量ξ的分布如表：若隨機變量ξ的期望值
E
（
ξ
）
=
1
2
，則D（2ξ+1）=
．

ξ -2 0 2

P a b
1
2

16．已知正項等差數列{a_n}的前n項和為S_n，且
21
∑
i
=
1
1
a
i
a
i
+
1
=
7
10
，a_n+2-a_n=
2
3
．
（1）求S_n；
（2）若b_n=（9a_n-29）?2^n-1，求數列{b_n}的前n項和T_n．

18．如圖，三棱柱ABC-A₁B₁C₁中，側面BB₁C₁C為菱形，B₁C的中點為O，AC=AB₁．

（1）文字敘述平面與平面垂直判定定理；
（2）求證：平面ABO⊥平面ACB₁．