北師大版（2019）必修第二冊《1.3 弧度制》2021年同步練習卷（3）

一、單選題

• 1．在單位圓中，200°的圓心角所對的弧長為（　　）

  A． 7 π 10

  B． 10 π 9

  C．9π

  D．10π
  組卷：486引用：2難度：0.9

  解析

• 2．30°的弧度數為（　　）

  A． π 2

  B． π 6

  C． π 4

  D． π 3
  組卷：518引用：3難度：0.9

  解析

• 3．已知集合A={第二象限角}，B={鈍角}，C={小于180°的角}，則A，B，C關系正確的是（　　）

  A．B=A∩C

  B．A?C

  C．B∪C=C

  D．A=B=C
  組卷：935引用：2難度：0.8

  解析

• 4．蚊香具有悠久的歷史，我國蚊香的發明與古人端午節的習俗有關．如圖，為某校數學社團用數學軟件制作的“蚊香”．畫法如下：在水平直線上取長度為1的線段AB，作一個等邊三角形ABC，然后以點B為圓心，AB為半徑逆時針畫圓弧交線段CB的延長線于點D（第一段圓弧），再以點C為圓心，CD為半徑逆時針畫圓弧交線段AC的延長線于點E，再以點A為圓心，AE為半徑逆時針畫圓弧…．以此類推，當得到的“蚊香”恰好有9段圓弧時，“蚊香”的長度為（　　）
  

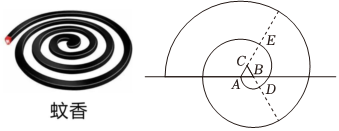
  A．14π

  B．18π

  C．24π

  D．30π
  組卷：308引用：10難度：0.7

  解析

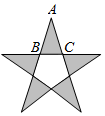• 5．德國著名的天文學家開普勒說過：“幾何學里有兩件寶，一個是勾股定理，另一個是黃金分割．如果把勾股定理比作黃金礦的話，那么可以把黃金分割比作鉆石礦，”黃金三角形有兩種，其中底與腰之比為黃金分割比的黃金三角形被認為是最美的三角形，它是兩底角為72°的等腰三角形（另一種是兩底角為36°的等腰三角形）．例如，五角星由五個黃金三角形與一個正五邊形組成，如圖所示，在其中一個黃金△ABC中，

  BC

  AC

  =

  5

  -

  1

  2

  ，根據這些信息，可得sin54°=（　　）

  A． 1 + 5 4

  B． 3 + 5 8

  C． 4 + 5 8

  D． 1 - 2 5 4
  組卷：91引用：4難度：0.7

  解析

• 6．坐標平面內點P的坐標為（sin5，cos5），則點P位于第（　　）象限．

  A．一

  B．二

  C．三

  D．四
  組卷：1088引用：7難度：0.8

  解析

• 7．自行車的大鏈輪有88齒，小鏈輪有20齒，當大鏈輪逆時針轉過一周時，小鏈輪轉過的弧度數是（　　）

  A． 5 π 11

  B． 44 π 5

  C． 5 π 22

  D． 22 π 5
  組卷：65引用：3難度：0.8

  解析

• 8．若角θ=120°，則角θ對應的弧度數是（　　）

  A． 2 π 3

  B． 3 π 4

  C． 7 π 12

  D． 5 π 6
  組卷：22引用：2難度：0.8

  解析

• 9．設計一個商標圖案如圖中陰影部分，矩形ABCD中，AB=2BC，且AB=8cm,以點A為圓心，AD為半徑作圓與BA的延長線相交于點F，則商標圖案的面積等于（　　）

  A．（4π+8）cm2

  B．（4π+16）cm2

  C．（3π+8）cm2

  D．（3π+16）cm2
  組卷：433引用：1難度：0.7

  解析

二、多選題

• 10．下列弧度與角度的轉化正確的是（　　）

  A． - 240 °= - 4 π 3

  B． 5 π 3 = 330 °

  C． 225 °= 5 π 4

  D． - 7 π 4 = - 310 °
  組卷：109引用：3難度：0.7

  解析

三、填空題

• 11．若兩個圓心角相同的扇形的面積之比為1：4，則這兩個扇形的周長之比為

  ．
  組卷：2引用：0難度：0.9

  解析

• 12．下列說法：①第二象限角比第一象限角大；②設θ是第二象限角，則

  tan

  θ

  2

  ＞

  cot

  θ

  2

  ；③三角形的內角是第一象限角或第二象限角；④函數y=sin|x|是最小正周期為π的周期函數；⑤在△ABC中，若sinA＞sinB，則A＞B．其中正確的是

  ．（寫出所有正確說法的序號）
  組卷：163引用：1難度：0.7

  解析

• 13．角α的終邊在第二、四象限的角平分線上，則角α的集合為

  （用弧度制表示）
  組卷：166引用：3難度：0.9

  解析

• 14．已知扇形的中心角為2弧度，扇形的半徑為3，則此扇形的弧長為

  ．
  組卷：129引用：1難度：0.8

  解析

四、解答題

• 15．設角α₁=-570°，α₂=750°，β₁=

  3

  5

  π，β₂=-

  7

  3

  π．
  （1）將α₁，α₂用弧度制表示出來，并指出它們各自所在的象限；
  （2）將β₁，β₂用角度制表示出來，并在-720°～0°之間找出與它們有相同終邊的所有角．
  組卷：31引用：2難度：0.6

  解析

• 16．把下列角度化成弧度：
  （1）22°30'；
  （2）-210°；
  （3）1200°．
  組卷：129引用：5難度：0.7

  解析

• 17．在0°～360°范圍內，找出與下列各角終邊相同的角，并判斷它們是第幾象限角．
  （1）-150°；
  （2）650°；
  （3）-950°15'．
  組卷：19引用：1難度：0.7

  解析

• 18．已知一扇形的圓心角為α，半徑為R，弧長為L（α＞0）．
  （1）已知扇形的周長為10cm,面積是4cm²，求扇形的圓心角；
  （2）若扇形周長為20cm,當扇形的圓心角α為多少弧度時，這個扇形的面積最大？
  組卷：64引用：2難度：0.7

  解析

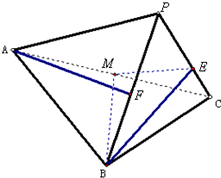• 19．在三棱錐P-ABC中，F，M分別是棱PB，AC的中點，E為PC上一動點．
  （1）若AF∥平面MEB，試確定點E的位置，并證明你的結論．
  （2）在滿足（1）的條件下，求三棱錐C-MEB與三棱錐C-PAB的體積比．
  組卷：32引用：1難度：0.3

  解析

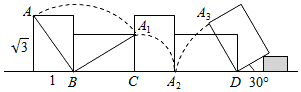• 20．如圖，已知一長為

  3

  dm,寬為1dm的長方形木塊在桌面上做無滑動的翻滾，翻滾到第三面時被一小木板擋住，使木塊底面與桌面成30°的角．求點A走過的路程及走過的弧所對應的扇形的總面積．
  組卷：105引用：2難度：0.9

  解析