當前位置：試卷中心 > 試卷詳情

2020-2021學年陜西省延安市富縣高級中學高一（下）期中數學試卷

發布：2025/6/29 16:0:14

一、選擇題（每小題5分，共60分）

1．函數y=
2
sinx
x
2
+
1
（x∈[-2，2]）的圖象大致為（　　）
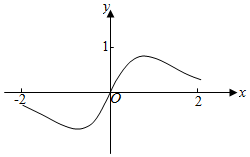
A． B．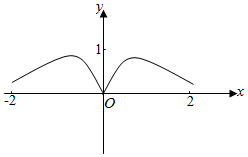
C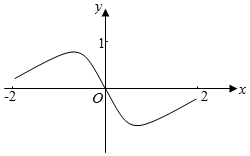． D．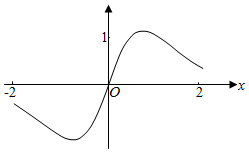
組卷：105引用：2難度：0.6
解析
2．函數f（x），g（x）由下列表格給出，則f（g（3））=（　　）

x 1 2 3 4

f（x） 2 4 3 1

g（x） 3 1 2 4

A．4 B．3 C．2 D．1
組卷：234引用：13難度：0.9
解析
3．已知函數f（x）=sin（2x+
π
6
），則要得到函數f（x）的圖象只需將函數g（x）=sin2x的圖象（　　）
A．向左平移
π
6
個單位長度
B．向右平移
π
6
個單位長度
C．向左平移
π
12
個單位長度
D．向右平移
π
12
個單位長度
組卷：43引用：5難度：0.9
解析
4．2019冠狀病毒病（CoronaVirusDisease2019（COVID-19））是由新型冠狀病毒（2019-nCoV）引發的疾病，目前全球感染者以百萬計．我國在黨中央、國務院、中央軍委的堅強領導下，已經率先控制住疫情，但目前疫情防控形勢依然嚴峻，湖北省中小學依然延期開學，所有學生按照停課不停學的要求，居家學習．小李同學在居家學習期間，從網上購買了一套高考數學沖刺模擬試卷，快遞員計劃在下午4：00～5：00之間送貨到小區門口的快遞柜中，小李同學父親參加防疫志愿服務，按規定，他換班回家的時間在下午4：30～5：00，則小李父親收到試卷無需等待的概率為（　　）
A．
1
8
B．
1
4
C．
3
4
D．
7
8
組卷：204引用：1難度：0.6
解析
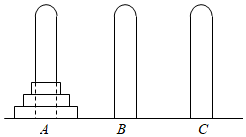5．古印度“漢諾塔問題”：一塊黃銅平板上裝著A，B，C三根金銅石細柱，其中細柱A上套著n個大小不等的環形金盤，大的在下、小的在上．將這些盤子全部轉移到另一根柱子上，移動規則如下：一次只能將一個金盤從一根柱子轉移到另外一根柱子上，不允許將較大盤子放在較小盤子上面．若A柱上現有3個金盤（如圖），將A柱上的金盤全部移到B柱上，至少需要移動次數為（　　）
A．5 B．7 C．9 D．11
組卷：84引用：4難度：0.4
解析
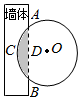6．“圓材埋壁”是《九章算術》中的一個問題：“今有圓材，埋在壁中，不知大小，以鋸鋸之，學會一寸，鋸道長一尺，問徑幾何？”其意為：今有一圓柱形木材，埋在墻壁中，不知道大小，用鋸取鋸它，鋸口深一寸，鋸道長一尺，問這塊圓柱形木材的直徑是多少？現有圓柱形木材一部分埋在墻壁中，截面如圖所示，已知弦AB=1尺，弓形高CD=1寸，則陰影部分面積約為（　　）（注：π≈3.14，sin22.5°≈
5
13
，1尺=10寸）
A．6.33平方寸 B．6.35平方寸 C．6.37平方寸 D．6.39平方寸
組卷：202引用：5難度：0.6
解析
7．若b＞a＞0，滿足tanα=
a
2
-
b
2
2
ab
，且sinα=
b
2
-
a
2
a
2
+
b
2
的角α的集合是（　　）
A．{α|0＜α＜
π
2
} B．{α|
π
2
+2kπ≤α≤π+2kπ，k∈Z}
C．{α|2kπ≤α≤π+2kπ，k∈Z} D．{α|
π
2
+2kπ＜α＜π+2kπ，k∈Z}
組卷：95引用：1難度：0.5
解析
8．函數y=2cosx+1（x∈[0，2π]）的單調遞減區間為（　　）
A．[0，2π] B．[0，π] C．[π，2π] D．
[
π
2
，
3
π
2
]
組卷：411引用：2難度：0.7
解析
9．要得到函數y=2sin（3x-
π
3
）的圖象，只需將函數y=2sin3x的圖象（　　）
A．向左平移
π
9
個單位 B．向左平移
π
3
個單位
C．向右平移
π
9
個單位 D．向右平移
π
3
個單位
組卷：231引用：2難度：0.8
解析
10．已知α為第二象限角，則（　　）
A．cosα-sinα＞0 B．sinα+cosα＞0
C．sin2α＜0 D．sinαtanα＞0
組卷：249引用：4難度：0.7
解析
11．半徑為4，圓心角為
π
4
的扇形的弧長為（　　）
A．
π
4
B．
π
2
C．π D．
3
π
4
組卷：469引用：3難度：0.9
解析
12．與角-330°終邊相同的最小正角是（　　）
A．-30° B．330° C．30° D．60°
組卷：1076引用：8難度：0.9
解析

二、填空題（每小題5分，共20分）

13．若f（x）≥h（x）=ax+b≥g（x），則定義h（x）為曲線f（x），g（x）的φ線．已知f（x）=tanx,
x∈[0，
π
2
），g（x）=sinx,x∈[0，
π
2
），則f（x），g（x）的φ線為
．
組卷：241引用：6難度：0.7
解析
14．若sin（x-
π
6
）=-
1
3
，則sin（2x+
π
6
）=
．
組卷：359引用：8難度：0.7
解析
15．已知數列{a_n}，a₁=1，a_n+1=
a
n
1
+
2
a
n
（n∈N^*），寫出這個數列的前4項，并根據規律，寫出這個數列的一個通項公式

．
組卷：13引用：1難度：0.5
解析
16．已知直線方程為
3
x
+
3
y
+
1
=
0
，則直線的傾斜角為
．
組卷：17引用：2難度：0.9
解析

三、解答題（共70分）

17．某校高一舉行了一次數學競賽，為了了解本次競賽學生的成績情況，從中抽取了部分學生的分數（得分取正整數，滿分為100）作為樣本（樣本容量為n）進行統計，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分組作出頻率分布直方圖，已知得分在[50，60），[90，100]的頻數分別為8，2．
（1）求樣本容量n和頻率分布直方圖中的x,y的值；
（2）估計本次競賽學生成績的中位數；
（3）在選取的樣本中，從競賽成績在80分以上（含80分）的學生中隨機抽取2名學生，求所抽取的2名學生中至少有一人得分在[90，100]內的概率．
組卷：615引用：9難度：0.3
解析
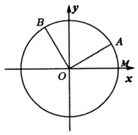18．如圖，已知單位圓O與x軸正半軸相交于點M，點A，B在單位圓上，其中點A在第一象限，且∠AOB=
π
2
，記∠MOA=α，∠MOB=β．
（Ⅰ）若α=
π
6
，求點A，B的坐標；
（Ⅱ）若點A的坐標為（
4
5
，m），求sinα-sinβ的值．
組卷：523引用：5難度：0.5
解析
19．求cos105°的值．
組卷：1引用：1難度：0.7
解析
20．（1）求
8
2
3
+
lg
3
1000
-
lg
3
的值；
（2）已知tanα=2，求
sin
（
π
+
α
）
-
sin
（
3
2
π
-
α
）
sin
（
π
-
α
）
+
2
cos
（
2
π
-
α
）
．
組卷：195引用：2難度：0.8
解析
21．已知函數
f
（
x
）
=
x
-
1
x
．
（1）判斷函數f（x）的奇偶性；
（2）根據定義證明函數
f
（
x
）
=
x
-
1
x
在區間
（
0
，
+
∞
）
上單調遞增．
組卷：390引用：6難度：0.7
解析
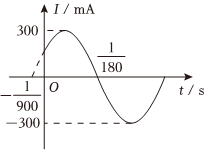22．某用電器電流I（mA）隨時間t（s）變化的關系式為
I
（
t
）
=
A
sin
（
ωt
+
φ
）
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
，如圖是其部分圖像．
（1）求I（t）=Asin（ωt+φ）的解析式；
（2）若該用電器核心部件有效工作的電流|I|必須大于150mA，則在1個周期內，該用電器核心部件的有效工作時間是多少？（電流的正負表示電流的正反方向）
組卷：8引用：1難度：0.5
解析

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．{α\|0＜α＜ π 2 }	B．{α\| π 2 +2kπ≤α≤π+2kπ，k∈Z}
C．{α\|2kπ≤α≤π+2kπ，k∈Z}	D．{α\| π 2 +2kπ＜α＜π+2kπ，k∈Z}

A．向左平移 π 9 個單位	B．向左平移 π 3 個單位
C．向右平移 π 9 個單位	D．向右平移 π 3 個單位

A．cosα-sinα＞0	B．sinα+cosα＞0
C．sin2α＜0	D．sinαtanα＞0

A．	B．
C．	D．

x	1	2	3	4
f（x）	2	4	3	1
g（x）	3	1	2	4

2020-2021學年陜西省延安市富縣高級中學高一（下）期中數學試卷

一、選擇題（每小題5分，共60分）

1．函數y=2sinxx2+1（x∈[-2，2]）的圖象大致為（ ）

2．函數f（x），g（x）由下列表格給出，則f（g（3））=（ ） x 1 2 3 4 f（x） 2 4 3 1 g（x） 3 1 2 4

3．已知函數f（x）=sin（2x+π6），則要得到函數f（x）的圖象只需將函數g（x）=sin2x的圖象（ ）

7．若b＞a＞0，滿足tanα=a2-b22ab，且sinα=b2-a2a2+b2的角α的集合是（ ）

8．函數y=2cosx+1（x∈[0，2π]）的單調遞減區間為（ ）

9．要得到函數y=2sin（3x-π3）的圖象，只需將函數y=2sin3x的圖象（ ）

10．已知α為第二象限角，則（ ）

11．半徑為4，圓心角為π4的扇形的弧長為（ ）

12．與角-330°終邊相同的最小正角是（ ）

二、填空題（每小題5分，共20分）

13．若f（x）≥h（x）=ax+b≥g（x），則定義h（x）為曲線f（x），g（x）的φ線．已知f（x）=tanx,x∈[0，π2），g（x）=sinx,x∈[0，π2），則f（x），g（x）的φ線為．

14．若sin（x-π6）=-13，則sin（2x+π6）=．

15．已知數列{an}，a1=1，an+1=an1+2an（n∈N*），寫出這個數列的前4項，并根據規律，寫出這個數列的一個通項公式 ．

16．已知直線方程為3x+3y+1=0，則直線的傾斜角為．

三、解答題（共70分）

18．如圖，已知單位圓O與x軸正半軸相交于點M，點A，B在單位圓上，其中點A在第一象限，且∠AOB=π2，記∠MOA=α，∠MOB=β．（Ⅰ）若α=π6，求點A，B的坐標；（Ⅱ）若點A的坐標為（45，m），求sinα-sinβ的值．

19．求cos105°的值．

20．（1）求823+lg31000-lg3的值；（2）已知tanα=2，求sin（π+α）-sin（32π-α）sin（π-α）+2cos（2π-α）．

21．已知函數f（x）=x-1x．（1）判斷函數f（x）的奇偶性；（2）根據定義證明函數f（x）=x-1x在區間（0，+∞）上單調遞增．

1．函數y=
2
sinx
x
2
+
1
（x∈[-2，2]）的圖象大致為（　　）

2．函數f（x），g（x）由下列表格給出，則f（g（3））=（　　）

x 1 2 3 4

f（x） 2 4 3 1

g（x） 3 1 2 4

3．已知函數f（x）=sin（2x+
π
6
），則要得到函數f（x）的圖象只需將函數g（x）=sin2x的圖象（　　）

7．若b＞a＞0，滿足tanα=
a
2
-
b
2
2
ab
，且sinα=
b
2
-
a
2
a
2
+
b
2
的角α的集合是（　　）

8．函數y=2cosx+1（x∈[0，2π]）的單調遞減區間為（　　）

9．要得到函數y=2sin（3x-
π
3
）的圖象，只需將函數y=2sin3x的圖象（　　）

10．已知α為第二象限角，則（　　）

11．半徑為4，圓心角為
π
4
的扇形的弧長為（　　）

12．與角-330°終邊相同的最小正角是（　　）

13．若f（x）≥h（x）=ax+b≥g（x），則定義h（x）為曲線f（x），g（x）的φ線．已知f（x）=tanx,
x∈[0，
π
2
），g（x）=sinx,x∈[0，
π
2
），則f（x），g（x）的φ線為
．

14．若sin（x-
π
6
）=-
1
3
，則sin（2x+
π
6
）=
．

15．已知數列{a_n}，a₁=1，a_n+1=
a
n
1
+
2
a
n
（n∈N^*），寫出這個數列的前4項，并根據規律，寫出這個數列的一個通項公式

．

16．已知直線方程為
3
x
+
3
y
+
1
=
0
，則直線的傾斜角為
．

18．如圖，已知單位圓O與x軸正半軸相交于點M，點A，B在單位圓上，其中點A在第一象限，且∠AOB=
π
2
，記∠MOA=α，∠MOB=β．
（Ⅰ）若α=
π
6
，求點A，B的坐標；
（Ⅱ）若點A的坐標為（
4
5
，m），求sinα-sinβ的值．

20．（1）求
8
2
3
+
lg
3
1000
-
lg
3
的值；
（2）已知tanα=2，求
sin
（
π
+
α
）
-
sin
（
3
2
π
-
α
）
sin
（
π
-
α
）
+
2
cos
（
2
π
-
α
）
．

21．已知函數
f
（
x
）
=
x
-
1
x
．
（1）判斷函數f（x）的奇偶性；
（2）根據定義證明函數
f
（
x
）
=
x
-
1
x
在區間
（
0
，
+
∞
）
上單調遞增．