當前位置：試卷中心 > 試卷詳情

2023-2024學年江西省贛州市立德虔州高級中學高三（下）期中數學試卷

發布：2025/6/29 16:0:15

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個選項中，只有一項是符合題目要求的。

1．若a=0.6e^0.4，b=2-ln4，c=e-2，則a,b,c 的大小關系為（　　）
A．a＞b＞c B．a＞c＞b C．b＞c＞a D．c＞b＞a
組卷：63引用：3難度：0.4
解析
2．已知
a
，
b
是兩個單位向量，且
?
a
，
b
?
=
60
°
，若
c
=
2
a
-
b
，則
cos
?
a
，
c
?
=（　　）
A．
1
2
B．
3
2
C．
1
3
D．
3
3
組卷：194引用：5難度：0.8
解析
3．已知a,b,c,均大于1，滿足
2
a
-
1
a
-
1
=
2
+
2
lo
g
2
a
,
3
b
-
2
b
-
1
=
3
+
3
lo
g
3
b
,
5
c
-
4
c
-
1
=
5
+
5
lo
g
5
c
，則下列不等式成立的是（　　）
A．c＜b＜a B．c＜a＜b C．a＜c＜b D．a＜b＜c
組卷：104引用：3難度：0.5
解析
4．在復平面內，復數
5
i
2
-
i
的對應點位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：546引用：12難度：0.9
解析
5．若直線l：y=x+b與曲線C：
x
=
2
-
y
2
有且僅有一個公共點，則實數b的取值范圍是（　　）
A．
（
-
2
，
2
]
∪
{
-
2
}
B．
[
-
2
，
2
]
∪
{
-
2
}
C．（-2，2） D．{-2，2}
組卷：221引用：4難度：0.5
解析
6．已知有限集X，Y，定義集合X-Y={x|x∈X，且x?Y}，|X|表示集合X中的元素個數．若x={1，2，3，4}，Y={3，4，5}，則|（X-Y）∪（Y-X）|=（　　）
A．3 B．4 C．5 D．6
組卷：132引用：2難度：0.6
解析
7．已知x+y=1，x＞0，y＞0，則
1
2
x
+
x
y
+
1
的最小值為（　　）
A．
4
3
B．
5
4
C．1 D．
2
3
3
組卷：387引用：3難度：0.5
解析
8．設S_n為數列{a_n}的前n項和，若2S_n=3a_n-3，則a₄=（　　）
A．27 B．81 C．93 D．243
組卷：319引用：5難度：0.7
解析

二、選擇題：本題共3小題，每小題6分，共18分。在每小題給出的四個選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。

9．已知數列{a_n}滿足a₁=2，a_n+1=
a
n
+
1
，
n
為奇數
a
n
+
3
，
n
為偶數
，
，記b_n=a_2n-1，則（　　）
A．b₁=3 B．b₂=6 C．b_n+1-b_n=4 D．b_n=4n+2
組卷：164引用：4難度：0.5
解析

10．已知函數
f
（
x
）
=
4
cos
（
2
x
-
π
3
）
，則（　　）

A．f（x）圖象的對稱中心為

（

kπ

，

）

，k∈Z

B．f（x）的單調遞減區間為

（

kπ

，

kπ

）

，k∈Z

C．為了得到函數y=4cos2x的圖象，可將f（x）的圖象上所有的點向左平移

個單位長度

D．為了得到函數y=4sin2x的圖象，可將f（x）的圖象上所有的點向右平移

個單位長度

組卷：33引用：2難度：0.8

解析

11．空氣質量指數分為“優”“良”“輕度污染”“中度污染”“重度污染”“嚴重污染”六個等級，指數越大說明污染的情況越嚴重，對人體危害越大，這六個等級分別對應的指數范圍為[0，50]，[51，100]，[101，150]，[151，200]，[201，300]，[301，500]，如圖是湘陰縣連續14天的空氣質量指數趨勢圖，下面說法正確的是（　　）

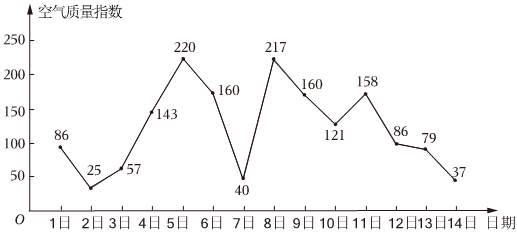
A．這14天中有4天空氣質量指數為“良”

B．從2日到5日空氣質量越來越差

C．這14天中空氣質量指數的中位數是103

D．連續三天中空氣質量指數方差最小的是9日到11日

組卷：6引用：3難度：0.7

解析

三、填空題：本題共3小題，每小題5分，共15分。

12．在正四棱柱ABCD-A₁B₁C₁D₁中，AB=1，AA₁=3，點M在棱BB₁上，BD₁⊥平面ACM，則三棱錐B-ACM的外接球的表面積為
．
組卷：17引用：1難度：0.5
解析
13．黨的十九大報告提出“鄉村振興戰略”，要“推動城鄉義務教育一體化發展，高度重視農村義務教育”．為了響應報告精神，某師范大學6名畢業生主動申請到某貧困山區的鄉村小學工作，若將這6名畢業生分配到該山區的3所鄉村小學，每所學校至少分配1人，則分配方案的總數為
．
組卷：295引用：5難度：0.6
解析
14．
（
y
x
-
1
）
（
2
x
+
y
）
5
的展開式中，x²y³的系數為
．（用數字作答）
組卷：243引用：6難度：0.8
解析

四、解答題：本題共5小題，共77分。解答應寫出文字說明、證明過程或演算步驟。

15．某少數民族的刺繡有著悠久的歷史，圖中（1）、（2）、（3）、（4）為她們刺繡最簡單的四個圖案，這些圖案都是由小正方形構成，小正方形數越多越漂亮，按同樣的規律刺繡（小正方形的擺放規律相同），設第n個圖形包含f（n）個小正方形．

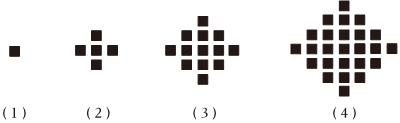
（1）求f（6）的值；
（2）求出f（n）的表達式．
組卷：17引用：1難度：0.5
解析
16．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0），離心率為
1
2
，短軸長為2
3
，A₁，A₂為橢圓的左、右頂點，P為橢圓上任一點（不同于A₁，A₂），直線A₁P，A₂P分別與直線l：x=4交于M，N兩點．
（1）求橢圓C的標準方程；
（2）若F為橢圓右焦點，試判斷
FM
?
FN
是否為定值，若為定值，求出該值；若不為定值，請說明理由．
組卷：71引用：1難度：0.5
解析
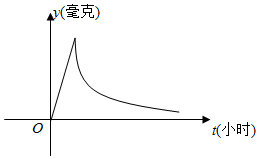17．為了預防流感，某學校對教室用藥熏消毒法進行消毒，已知藥物釋放過程中，室內每立方米空氣中含藥量y（毫克）與時間t（小時）成正比．已知6分鐘后藥物釋放完畢，藥物釋放完畢后，y與t的函數關系是為y=（
1
16
）

t
-
1
10
，如圖所示，根據圖中提供的信息，回答下列問題：
（1）求從藥物釋放開始，每立方米空氣中的含藥量y（毫克）與時間t（小時）之間的函數關系式；
（2）據測定，當空氣中每立方米的含藥量降低到0.125毫克以下時，學生方可進教室，那么從藥物釋放開始，至少需要經過多少分鐘后，學生才能回到教室？
組卷：51引用：1難度：0.5
解析
18．為了解某市區高中學生的閱讀時間，從該市區隨機抽取了800名學生進行調查，得到了這800名學生一周的平均閱讀時間（單位：小時），并將樣本數據分成九組，繪制成如圖所示的頻率分布直方圖．

（1）求a的值；
（2）為進一步了解這800名學生閱讀時間的分配情況，從周平均閱讀時間在（12，14]，（14，16]，（16，18]三組內的學生中，采用分層抽樣的方法抽取了10人，現從這10人中隨機抽取3人，記周平均閱讀時間在（14，16]內的學生人數為X，求X的分布列和數學期望；
（3）以樣本的頻率估計概率，從該市區學生周平均閱讀時間在（8，14]內中隨機抽取20名學生．這20名學生中，周平均閱讀時間在（10，12]內的學生最可能有多少名？
組卷：80引用：5難度：0.5
解析
19．已知f（x）=e^x-ax-1．
（1）當a=2時，討論f（x）的單調區間；
（2）若f（x）在定義域R內單調遞增，求a的取值范圍．
組卷：207引用：7難度：0.7
解析