精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

當前位置：試卷中心 > 試卷詳情

2019-2020學年廣西河池市高二（下）期末數學試卷（理科）

發布：2025/10/6 18:0:20

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．在等差數列{a_n}中，2a₅₁₀-a₈=4，則{a_n}的前2023項和S₂₀₂₃=（　　）
A．2023 B．4046 C．6069 D．8092
組卷：75引用：3難度：0.8
2．如圖為某幾何體的三視圖（圖中網格紙上每個小正方形的邊長為1），則該幾何體的體積等于（　　）
A．π+12 B．
5
π
3
+
12
C．π+4 D．
5
π
3
+
4
組卷：33引用：5難度：0.7
3．若雙曲線
x
2
a
2
+
y
2
b
2
=1（a＞0，b＞0）的漸近線與拋物線y=x²+1相切，則此雙曲線的離心率為（　　）
A．
3
B．2 C．
5
D．3
組卷：14引用：2難度：0.6
4．設A，B為直線y=x與圓x²+y²=1的兩個交點，則|AB|=（　　）
A．1 B．
2
C．
3
D．2
組卷：694引用：21難度：0.9
5．若a=log₃0.6，b=3^0.6，c=0.6³，則a,b,c的大小關系為（　　）
A．a＜c＜b B．c＜a＜b C．b＜a＜c D．a＜b＜c
組卷：49引用：2難度：0.9
6．函數f（x）的圖象如圖所示，下列數值排序正確的是（　　）
A．0＜f'（2）＜f'（3）＜f（3）-f（2）
B．0＜f'（3）＜f（3）-f（2）＜f'（2）
C．0＜f'（3）＜f'（2）＜f（3）-f（2）
D．0＜f（3）-f（2）＜f'（2）＜f'（3）
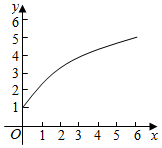組卷：107引用：11難度：0.7
7．已知z∈C，且（z-i）?（
z
+i）=1，i為虛數單位，則|z-3-5i|的最大值是（　　）
A．5 B．6 C．7 D．8
組卷：101引用：1難度：0.7
8．已知集合A={1，2，3，4，5，6}，a∈A，b∈A，則“使函數f（x）=ln（x²+ax+b）的定義域為R”的概率為（　　）
A．
13
36
B．
15
36
C．
17
36
D．
19
36
組卷：90引用：2難度：0.9
9．若sin2a=
2
2
，則sin⁴a+cos⁴a的值是（　　）
A．
1
2
B．
3
5
C．
2
-
2
2
D．
3
4
組卷：36引用：7難度：0.9
10．已知函數f（x）=sin（ωx+φ）在區間
（
π
6
，
2
π
3
）
單調遞增，直線
x
=
π
6
和
x
=
2
π
3
為函數y=f（x）的圖象的兩條對稱軸，則f（0）=（　　）
A．
-
3
2
B．
-
1
2
C．
1
2
D．
3
2
組卷：266引用：6難度：0.7

11．下面幾種推理過程是演繹推理的是（　　）

A．兩條直線平行，同旁內角互補，如果∠A與∠B是兩條平行直線的同旁內角，則∠A+∠B=180°

B．某校高三（1）班有55人，（2）班有54人，（3）班有52人，由此得高三所有班人數超過50人

C．由平面三角形的性質，推測空間四面體的性質

D．在數列{a_n}中，a₁=1，a_n=

（a_n-1+

）（n≥2），由此歸納出{a_n}的通項公式

組卷：78引用：12難度：0.9

12．已知集合A={x|x²+2x-8≥0}，B={x|-2＜x＜3}，則A∩B=（　　）
A．（2，3） B．[2，3） C．[-4，2] D．（-4，3）
組卷：641引用：6難度：0.8

二、填空題：本大題共4小題，每小題5分，共20分.

13．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左焦點為F，過點F且與C的一條漸近線平行的直線l與圓x²+y²=a²相交于A，B兩點，且|AB|=b,則C的離心率為
．
組卷：45引用：3難度：0.5
14．若向量
a
=（1，x），
b
=（2，1），滿足條件
a
⊥
b
，則x=
．
組卷：38引用：4難度：0.7
15．設x,y滿足條件
y
≥
1
x
+
y
≤
2
x
-
2
y
+
4
≥
0
，則z=x+2y的最大值為
．
組卷：7引用：4難度：0.6
16．M是圓C：x²+y²=1上的動點，點N（2，0），則線段MN的中點P的軌跡方程是
．
組卷：12引用：3難度：0.5

三、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

17．已知各項均為正數的數列{a_n}的前n項和為S_n，且對任意的n∈N^*，都有2S_n=n²+n.
（Ⅰ）求數列{a_n}的通項公式；
（Ⅱ）數列{b_n}滿足b₁=1，2b_n+1-b_n=0（n∈N^*），若c_n=a_nb_n，求數列{c_n}的前n項和為T_n；
（Ⅲ）在（Ⅱ）的條件下，問是否存在整數m,使得對任意的正整數n,都有m-2＜T_n＜m+2，若存在，求出m的值，若不存在，說明理由．
組卷：28引用：1難度：0.3
18．如圖，PO是三棱錐P-ABC的高，PA=PB，AB⊥AC，E是PB的中點．
（1）求證：OE∥平面PAC；
（2）若∠ABO=∠CBO=30°，PO=3，PA=5．
①求二面角C-AE-B所成平面角的正弦值．
②在線段CE上是否存在一點M，使得直線MO與平面BCP所成角為30°？
組卷：126引用：1難度：0.3
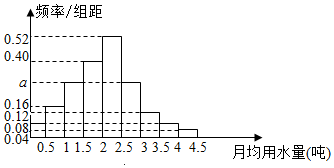19．我國是世界上嚴重缺水的國家，城市缺水問題較為突出．某市政府為了鼓勵居民節約用水，計劃在本市試行居民生活用水定額管理，即確定一個合理的居民月用水量標準x（噸），用水量不超過x的部分按平價收費，超出x的部分按議價收費．為了了解全市居民用水量的分布情況，通過抽樣，獲得了100位居民某年的月均用水量（單位：噸），將數據按照[0，0.5），[0.5，1），…，[4，4.5]分成9組，制成了如圖所示的頻率分布直方圖．
（Ⅰ）求直方圖中a的值；
（Ⅱ）若該市政府希望使85%的居民每月的用水量不超過標準x（噸），估計x的值，并說明理由；
（Ⅲ）已知平價收費標準為4元/噸，議價收費標準為8元/噸．當x=3時，估計該市居民的月平均水費．（同一組中的數據用該組區間的中點值代替）
組卷：119引用：3難度：0.1
20．設函數f（x）=e^mx+x²-mx.
（1）證明：f（x）在（-∞，0）單調遞減，在（0，+∞）單調遞增；
（2）若對于任意x₁，x₂∈[-1，1]，都有|f（x₁）-f（x₂）|≤e-1，求m的取值范圍．
組卷：2369引用：29難度：0.3
21．在△ABC中，A，B，C的對邊分別為a,b,c,acosB-2acosC=（2c-b）cosA．
（1）若c=
3
a,求cosB的值；
（2）若b=1，∠BAC的平分線AD交BC于點D，求AD長度的取值范圍．
組卷：1786引用：14難度：0.6
22．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（a＞0，b＞0）的右焦點F在直線2x-y-2=0上，A，B分別為C的左、右頂點，且|AF|=3|BF|．
（1）求C的標準方程；
（2）過點D（4，0）的直線l與C交于P，Q兩點，線段PQ的中點為N，若直線AN的斜率為
2
5
，求直線l的斜率．
組卷：54引用：2難度：0.4

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2019-2020學年廣西河池市高二（下）期末數學試卷（理科）

一、選擇題：本大題共12小題，每小題5分，共60分.在每小題給出的四個選項中，只有一項是符合題目要求的.

1．在等差數列{an}中，2a510-a8=4，則{an}的前2023項和S2023=（ ）

2．如圖為某幾何體的三視圖（圖中網格紙上每個小正方形的邊長為1），則該幾何體的體積等于（ ）

3．若雙曲線x2a2+y2b2=1（a＞0，b＞0）的漸近線與拋物線y=x2+1相切，則此雙曲線的離心率為（ ）

4．設A，B為直線y=x與圓x2+y2=1的兩個交點，則|AB|=（ ）

5．若a=log30.6，b=30.6，c=0.63，則a,b,c的大小關系為（ ）

6．函數f（x）的圖象如圖所示，下列數值排序正確的是（ ）

7．已知z∈C，且（z-i）?（z+i）=1，i為虛數單位，則|z-3-5i|的最大值是（ ）

8．已知集合A={1，2，3，4，5，6}，a∈A，b∈A，則“使函數f（x）=ln（x2+ax+b）的定義域為R”的概率為（ ）

9．若sin2a=22，則sin4a+cos4a的值是（ ）

10．已知函數f（x）=sin（ωx+φ）在區間（π6，2π3）單調遞增，直線x=π6和x=2π3為函數y=f（x）的圖象的兩條對稱軸，則f（0）=（ ）

11．下面幾種推理過程是演繹推理的是（ ）

12．已知集合A={x|x2+2x-8≥0}，B={x|-2＜x＜3}，則A∩B=（ ）

二、填空題：本大題共4小題，每小題5分，共20分.

13．已知雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左焦點為F，過點F且與C的一條漸近線平行的直線l與圓x2+y2=a2相交于A，B兩點，且|AB|=b,則C的離心率為 ．

14．若向量a=（1，x），b=（2，1），滿足條件a⊥b，則x=．

15．設x,y滿足條件y≥1x+y≤2x-2y+4≥0，則z=x+2y的最大值為 ．

16．M是圓C：x2+y2=1上的動點，點N（2，0），則線段MN的中點P的軌跡方程是 ．

三、解答題：本大題共6小題，共70分.解答應寫出必要的文字說明、證明過程及演算步驟.

18．如圖，PO是三棱錐P-ABC的高，PA=PB，AB⊥AC，E是PB的中點．（1）求證：OE∥平面PAC；（2）若∠ABO=∠CBO=30°，PO=3，PA=5．①求二面角C-AE-B所成平面角的正弦值．②在線段CE上是否存在一點M，使得直線MO與平面BCP所成角為30°？

20．設函數f（x）=emx+x2-mx.（1）證明：f（x）在（-∞，0）單調遞減，在（0，+∞）單調遞增；（2）若對于任意x1，x2∈[-1，1]，都有|f（x1）-f（x2）|≤e-1，求m的取值范圍．

21．在△ABC中，A，B，C的對邊分別為a,b,c,acosB-2acosC=（2c-b）cosA．（1）若c=3a,求cosB的值；（2）若b=1，∠BAC的平分線AD交BC于點D，求AD長度的取值范圍．

1．在等差數列{a_n}中，2a₅₁₀-a₈=4，則{a_n}的前2023項和S₂₀₂₃=（　　）

2．如圖為某幾何體的三視圖（圖中網格紙上每個小正方形的邊長為1），則該幾何體的體積等于（　　）

3．若雙曲線
x
2
a
2
+
y
2
b
2
=1（a＞0，b＞0）的漸近線與拋物線y=x²+1相切，則此雙曲線的離心率為（　　）

4．設A，B為直線y=x與圓x²+y²=1的兩個交點，則|AB|=（　　）

5．若a=log₃0.6，b=3^0.6，c=0.6³，則a,b,c的大小關系為（　　）

6．函數f（x）的圖象如圖所示，下列數值排序正確的是（　　）

7．已知z∈C，且（z-i）?（
z
+i）=1，i為虛數單位，則|z-3-5i|的最大值是（　　）

8．已知集合A={1，2，3，4，5，6}，a∈A，b∈A，則“使函數f（x）=ln（x²+ax+b）的定義域為R”的概率為（　　）

9．若sin2a=
2
2
，則sin⁴a+cos⁴a的值是（　　）

10．已知函數f（x）=sin（ωx+φ）在區間
（
π
6
，
2
π
3
）
單調遞增，直線
x
=
π
6
和
x
=
2
π
3
為函數y=f（x）的圖象的兩條對稱軸，則f（0）=（　　）

11．下面幾種推理過程是演繹推理的是（　　）

12．已知集合A={x|x²+2x-8≥0}，B={x|-2＜x＜3}，則A∩B=（　　）

13．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左焦點為F，過點F且與C的一條漸近線平行的直線l與圓x²+y²=a²相交于A，B兩點，且|AB|=b,則C的離心率為
．

14．若向量
a
=（1，x），
b
=（2，1），滿足條件
a
⊥
b
，則x=
．

15．設x,y滿足條件
y
≥
1
x
+
y
≤
2
x
-
2
y
+
4
≥
0
，則z=x+2y的最大值為
．

16．M是圓C：x²+y²=1上的動點，點N（2，0），則線段MN的中點P的軌跡方程是
．

18．如圖，PO是三棱錐P-ABC的高，PA=PB，AB⊥AC，E是PB的中點．
（1）求證：OE∥平面PAC；
（2）若∠ABO=∠CBO=30°，PO=3，PA=5．
①求二面角C-AE-B所成平面角的正弦值．
②在線段CE上是否存在一點M，使得直線MO與平面BCP所成角為30°？

20．設函數f（x）=e^mx+x²-mx.
（1）證明：f（x）在（-∞，0）單調遞減，在（0，+∞）單調遞增；
（2）若對于任意x₁，x₂∈[-1，1]，都有|f（x₁）-f（x₂）|≤e-1，求m的取值范圍．

21．在△ABC中，A，B，C的對邊分別為a,b,c,acosB-2acosC=（2c-b）cosA．
（1）若c=
3
a,求cosB的值；
（2）若b=1，∠BAC的平分線AD交BC于點D，求AD長度的取值范圍．