當前位置：試卷中心 > 試卷詳情

2020-2021學年黑龍江省八校高二（上）期中數學試卷

發布：2025/10/6 19:0:16

一、選擇題（本大題共12小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．用“輾轉相除法”求得360和504的最大公約數是（　　）
A．72 B．36 C．24 D．2520
組卷：29引用：9難度：0.9
2．已知
1
4
＜
a
＜
2
3
，則關于x的方程
x
2
-
（
a
+
1
）
x
+
1
4
a
2
+
1
2
=
0
有解的概率為（　　）
A．
2
5
B．
1
8
C．
3
4
D．
1
6
組卷：56引用：4難度：0.7
3．已知a＞0，b＞0，若a+b=4，則（　　）
A．a²+b²有最小值 B．
ab
有最小值
C．
1
a
+
1
b
有最大值 D．
1
a
+
b
有最大值
組卷：2991引用：16難度：0.7
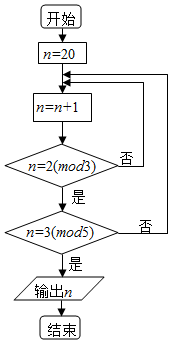4．中國古代數學著作《孫子算經》中有這樣一道算術題：“今有物不知其數，三三數之余二，五五數之余三，問物幾何？”人們把此類題目稱為“中國剩余定理”，若正整數N除以正整數m后的余數為n,則記為N=n（modm），例如11=2（mod3）．現將該問題以程序框圖的算法給出，執行該程序框圖，則輸出的n等于（　　）
A．21 B．22 C．23 D．24
組卷：129引用：27難度：0.9
5．已知△ABC中，
（
AB
?
BC
）
：
（
BC
?
CA
）
：
（
CA
?
AB
）
=
1
：
2
：
3
，則△ABC的形狀為（　　）
A．．鈍角三角形 B．等邊三角形
C．直角三角形 D．非等腰銳角三角形
組卷：22引用：2難度：0.9
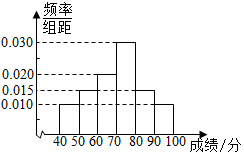6．在某次高中學科競賽中，4000名考生的參賽成績統計如圖所示，60分以下視為不及格，若同一組中數據用該組區間中點作代表，則下列說法中有誤的是（　　）
A．成績在[70，80]分的考生人數最多
B．考生競賽成績的中位數為75分
C．不及格的考生人數為1000人
D．考生競賽成績的平均分約70.5分
組卷：126引用：4難度：0.7
7．如圖所示的程序框圖運行的結果為（　　）
A．1022 B．1024 C．2044 D．2048
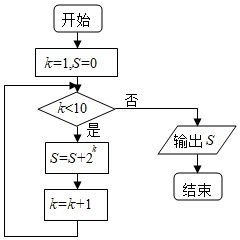組卷：34引用：6難度：0.9
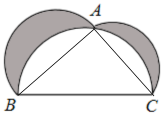8．如圖來自古希臘數學家希波克拉底所研究的幾何圖形，此圖由三個半圓構成，三個半圓的直徑分別為直角△ABC的斜邊BC，直角邊AB，AC．若AB=4，AC=3，在整個圖形中隨機取一點，則此點取自陰影部分的概率為（π≈3）（　　）
A．
23
25
B．
16
25
C．
25
41
D．
16
41
組卷：20引用：1難度：0.5
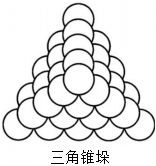9．朱世杰（1249年-1314年），字漢卿，號松庭，元代數學家、教育家，畢生從事數學教育，有“中世紀世界最偉大的數學家”之譽．他的一部名著《算學啟蒙》是中國最早的科普著作，該書中有名的是“堆垛問題”，其中有一道問題如下：今有三角錐垛果子，每面底子四十四個，問共積幾何？含義如下：把一樣大小的果子堆垛成正三棱錐形（如圖所示，給出了5層三角錐垛俯視示意圖），底面每邊44個果子，頂部僅一個果子，從頂層向下數，每
層的果子數分別為1，3，6，10，15，21，…，共有44層，問全垛共有多少個果子？則該三角錐垛從頂層向下數前40層的果子總數為（　　）
（參考公式：1+2²+3²+…+n²=
1
6
n（n+1）（2n+1））
A．12 341 B．11 480 C．10 280 D．8 436
組卷：66引用：3難度：0.6
10．側棱長為
2
3
的正四棱錐V-ABCD內，有一半球，其大圓面落在正四棱錐底面上，且與正四棱錐的四個側面相切，當正四棱錐的體積最大時，該半球的半徑為（　　）
A．1 B．
2
C．
2
2
D．2
組卷：203引用：2難度：0.5

11．下列有關一元線性回歸分析的命題正確的是（　　）

A．在兒子身高Y關于父親身高x的經驗回歸方程

957

839

中，若父親身高每增加1cm,其兒子身高平均增加約0.839cm

B．經驗回歸直線是經過散點圖中樣本數據點最多的那條直線

C．若兩個變量的線性相關程度越強，則樣本相關系數r就越接近于1

D．若甲、乙兩個模型的決定系數R²分別為0.87和0.78，則模型乙的擬合效果更好

組卷：224引用：3難度：0.7

12．用秦九韶算法計算多項式f（x）=x⁶-12x⁵+60x⁴-160x³+240x²-192x+64，當x=2時，v₃的值為（　　）
A．0 B．-32 C．80 D．-80
組卷：318引用：9難度：0.9

二、填空題（本大題共4小題，每小題5分，共20分，將答案填在題中的橫線上）

13．一組數據從小到大排列為：1，2，a,5，且中位數是3，則其方差大小是
．
組卷：68引用：2難度：0.8
14．在△ABC中，已知B=120°，
AC
=
19
，AB=2，則BC=
．
組卷：132引用：3難度：0.8
15．設一個正方體與底面邊長為2
3
，側棱長為
10
的正四棱錐的體積相等，則該正方體的棱長為

．
組卷：279引用：2難度：0.7
16．遠古時期，人們通過在繩子上打結來記錄數量，即“結繩計數”如圖所示的是一位母親記錄的孩子自出生后的天數，在從右向左依次排列的不同繩子上打結，滿六進一，根據圖示可知，孩子已經出生的天數是
．
組卷：112引用：1難度：0.8

三、解答題（本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟）

17．△ABC中，三個內角A、B、C所對的邊分別為a、b、c,若B=60°，a=（
3
-1）c.
（1）求角A的大小；
（2）已知當x∈[
π
6
，
π
2
]時，函數f（x）=cos2x+asinx的最大值為3，求△ABC的面積．
組卷：56引用：11難度：0.5

18．某印刷企業為了研究某種圖書每冊的成本費y（單位：元）與印刷數量x（單位：千冊）的關系，收集了一些數據并進行了初步整理，得到了下面的散點圖及一些統計量的值．

x

y

u

7
∑
i
=
1
（
x
i
-
x
）
2

7
∑
i
=
1
（
x
i
-
x
）
（
y
i
-
y
）

7
∑
i
=
1
（
u
i
-
u
）
2

7
∑
i
=
1
（
u
i
-
u
）
（
y
i
-
y
）

5 3.5 0.2 2 30 0.7 7

表中
u
i
=
1
x
i
，
u
=
1
7
7
∑
i
=
1
u
i
．
（1）根據散點圖判斷：y=a+bx與
y
=
c
+
d
x
哪一個模型更適合作為該圖書每冊的成本費y與印刷數量x的回歸方程？（只要求給出判斷，不必說明理由）
（2）根據（1）的判斷結果及表中數據建立y關于x的回歸方程（結果精確到0.1）；
（3）若該圖書每冊的定價為9元，則至少應該印刷多少冊，才能使銷售利潤不低于80000元（假設能夠全部售出）．
附：對于一組數據（ω₁，v₁），（ω₂，v₂），…，（ω_n，v_n），其回歸直線v=βω+α的斜率和截距的最小二乘法估計分別為：
?
β
=
m
∑
i
=
1
（
ω
i
-
ω
）
（
v
i
-
v
）
m
∑
i
=
1
（
ω
i
-
ω
）
2
，
?
α
=
v
-
?
β
ω
．

組卷：280引用：2難度：0.6

19．已知數列{a_n}滿足a₁=1，a_n=3a_n-1+4（n≥2）．
（1）求證：數列{a_n+2}是等比數列；
（2）求數列{a_n}的通項公式；
（3）寫出
5
∑
i
=
1
a
2
i
-
1
的具體展開式，并求其值．
組卷：281引用：3難度：0.6

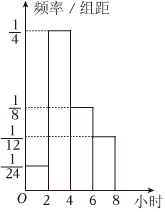20．4月23日是世界讀書日，樹人中學為了解本校學生課外閱讀情況，按性別進行分層，用分層隨機抽樣的方法從全校學生中抽出一個容量為100的樣本，其中男生40名，女生60名．經調查統計，分別得到40名男生一周課外閱讀時間（單位：小時）的頻數分布表和60名女生一周課外閱讀時間（單位：小時）的頻率分布直方圖．（以各組的區間中點值代表該組的各個值）

男生一周課外閱讀時間頻數分布表

小時頻數

[0，2] 9

[2，4] 25

[4，6] 3

[6，8] 3

女生一周課外閱讀時間頻率分布直方圖
（1）從一周課外閱讀時間為[4，6]的學生中按比例分配抽取6人，再從這6名學生中選出2名同學調查他們閱讀書目．求這兩人都是女生的概率；
（2）分別估計男生和女生一周課外閱讀時間的平均數
x
，
y
；
（3）估計總樣本的平均數
Z
和方差s²．
參考數據和公式：男生和女生一周課外閱讀時間方差的估計值分別為
S
2
男
=
2
.
4
和
S
2
女
=
3

S
2
=
1
100
[
40
∑
i
=
1
（
x
i
-
x
）
2
+
40
∑
i
=
1
（
x
i
-
z
）
2
+
60
∑
i
=
1
（
y
i
-
y
）
+
60
∑
i
=
1
（
y
i
-
z
）
]

x?（1≤i≤40）和y?（1≤i≤60）分別表示男生和女生一周閱讀時間的樣本，其中i∈Z．

組卷：35引用：1難度：0.7

21．已知△ABC是等邊三角形，點M，N滿足
AB
=
3
AM
，
CA
=
3
CN
，將△AMN沿MN折起到△A'MN的位置，使∠A'MB=90°．
（1）求證：A'M⊥平面MBCN；
（2）在線段BC上是否存在點D，使平面A'ND與平面A'MB夾角的余弦值為
39
13
？若存在，求
|
BD
|
|
DC
|
的值；若不存在，說明理由．
組卷：42引用：1難度：0.4
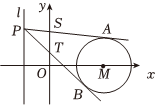22．如圖，已知圓M：x²+y²-4x+3=0，點P（-1，t）為直線l：x=-1上一動點，
過點P引圓M的兩條切線，切點分別為A，B．
（1）t=1時，求直線PA、PB方程（點A在點B上方）；
（2）若兩條切線PA，PB與y軸分別交于S，T兩點，求|ST|的最小值．
組卷：55引用：1難度：0.4

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．a²+b²有最小值	B． ab 有最小值
C． 1 a + 1 b 有最大值	D． 1 a + b 有最大值

A．．鈍角三角形	B．等邊三角形
C．直角三角形	D．非等腰銳角三角形

x	y	u	7 ∑ i = 1 （ x i - x ） 2	7 ∑ i = 1 （ x i - x ）（ y i - y ）	7 ∑ i = 1 （ u i - u ） 2	7 ∑ i = 1 （ u i - u ）（ y i - y ）
5	3.5	0.2	2	30	0.7	7

男生一周課外閱讀時間頻數分布表
小時	頻數
[0，2]	9
[2，4]	25
[4，6]	3
[6，8]	3

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2020-2021學年黑龍江省八校高二（上）期中數學試卷

一、選擇題（本大題共12小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項是符合題目要求的）

1．用“輾轉相除法”求得360和504的最大公約數是（ ）

2．已知14＜a＜23，則關于x的方程x2-（a+1）x+14a2+12=0有解的概率為（ ）

3．已知a＞0，b＞0，若a+b=4，則（ ）

5．已知△ABC中，（AB?BC）：（BC?CA）：（CA?AB）=1：2：3，則△ABC的形狀為（ ）

6．在某次高中學科競賽中，4000名考生的參賽成績統計如圖所示，60分以下視為不及格，若同一組中數據用該組區間中點作代表，則下列說法中有誤的是（ ）

7．如圖所示的程序框圖運行的結果為（ ）

8．如圖來自古希臘數學家希波克拉底所研究的幾何圖形，此圖由三個半圓構成，三個半圓的直徑分別為直角△ABC的斜邊BC，直角邊AB，AC．若AB=4，AC=3，在整個圖形中隨機取一點，則此點取自陰影部分的概率為（π≈3）（ ）

10．側棱長為23的正四棱錐V-ABCD內，有一半球，其大圓面落在正四棱錐底面上，且與正四棱錐的四個側面相切，當正四棱錐的體積最大時，該半球的半徑為（ ）

11．下列有關一元線性回歸分析的命題正確的是（ ）

12．用秦九韶算法計算多項式f（x）=x6-12x5+60x4-160x3+240x2-192x+64，當x=2時，v3的值為（ ）

二、填空題（本大題共4小題，每小題5分，共20分，將答案填在題中的橫線上）

13．一組數據從小到大排列為：1，2，a,5，且中位數是3，則其方差大小是 ．

14．在△ABC中，已知B=120°，AC=19，AB=2，則BC=．

15．設一個正方體與底面邊長為23，側棱長為10的正四棱錐的體積相等，則該正方體的棱長為 ．

16．遠古時期，人們通過在繩子上打結來記錄數量，即“結繩計數”如圖所示的是一位母親記錄的孩子自出生后的天數，在從右向左依次排列的不同繩子上打結，滿六進一，根據圖示可知，孩子已經出生的天數是．

三、解答題（本大題共6小題，共70分，解答應寫出文字說明、證明過程或演算步驟）

17．△ABC中，三個內角A、B、C所對的邊分別為a、b、c,若B=60°，a=（3-1）c.（1）求角A的大小；（2）已知當x∈[π6，π2]時，函數f（x）=cos2x+asinx的最大值為3，求△ABC的面積．

19．已知數列{an}滿足a1=1，an=3an-1+4（n≥2）．（1）求證：數列{an+2}是等比數列；（2）求數列{an}的通項公式；（3）寫出5∑i=1a2i-1的具體展開式，并求其值．

22．如圖，已知圓M：x2+y2-4x+3=0，點P（-1，t）為直線l：x=-1上一動點，過點P引圓M的兩條切線，切點分別為A，B．（1）t=1時，求直線PA、PB方程（點A在點B上方）；（2）若兩條切線PA，PB與y軸分別交于S，T兩點，求|ST|的最小值．

1．用“輾轉相除法”求得360和504的最大公約數是（　　）

2．已知
1
4
＜
a
＜
2
3
，則關于x的方程
x
2
-
（
a
+
1
）
x
+
1
4
a
2
+
1
2
=
0
有解的概率為（　　）

3．已知a＞0，b＞0，若a+b=4，則（　　）

5．已知△ABC中，
（
AB
?
BC
）
：
（
BC
?
CA
）
：
（
CA
?
AB
）
=
1
：
2
：
3
，則△ABC的形狀為（　　）

6．在某次高中學科競賽中，4000名考生的參賽成績統計如圖所示，60分以下視為不及格，若同一組中數據用該組區間中點作代表，則下列說法中有誤的是（　　）

7．如圖所示的程序框圖運行的結果為（　　）

8．如圖來自古希臘數學家希波克拉底所研究的幾何圖形，此圖由三個半圓構成，三個半圓的直徑分別為直角△ABC的斜邊BC，直角邊AB，AC．若AB=4，AC=3，在整個圖形中隨機取一點，則此點取自陰影部分的概率為（π≈3）（　　）

10．側棱長為
2
3
的正四棱錐V-ABCD內，有一半球，其大圓面落在正四棱錐底面上，且與正四棱錐的四個側面相切，當正四棱錐的體積最大時，該半球的半徑為（　　）

11．下列有關一元線性回歸分析的命題正確的是（　　）

12．用秦九韶算法計算多項式f（x）=x⁶-12x⁵+60x⁴-160x³+240x²-192x+64，當x=2時，v₃的值為（　　）

13．一組數據從小到大排列為：1，2，a,5，且中位數是3，則其方差大小是
．

14．在△ABC中，已知B=120°，
AC
=
19
，AB=2，則BC=
．

15．設一個正方體與底面邊長為2
3
，側棱長為
10
的正四棱錐的體積相等，則該正方體的棱長為

．

16．遠古時期，人們通過在繩子上打結來記錄數量，即“結繩計數”如圖所示的是一位母親記錄的孩子自出生后的天數，在從右向左依次排列的不同繩子上打結，滿六進一，根據圖示可知，孩子已經出生的天數是
．

17．△ABC中，三個內角A、B、C所對的邊分別為a、b、c,若B=60°，a=（
3
-1）c.
（1）求角A的大小；
（2）已知當x∈[
π
6
，
π
2
]時，函數f（x）=cos2x+asinx的最大值為3，求△ABC的面積．

19．已知數列{a_n}滿足a₁=1，a_n=3a_n-1+4（n≥2）．
（1）求證：數列{a_n+2}是等比數列；
（2）求數列{a_n}的通項公式；
（3）寫出
5
∑
i
=
1
a
2
i
-
1
的具體展開式，并求其值．

22．如圖，已知圓M：x²+y²-4x+3=0，點P（-1，t）為直線l：x=-1上一動點，
過點P引圓M的兩條切線，切點分別為A，B．
（1）t=1時，求直線PA、PB方程（點A在點B上方）；
（2）若兩條切線PA，PB與y軸分別交于S，T兩點，求|ST|的最小值．