2023-2024學年浙江省臺州市椒江區(qū)北師大臺州附中高一（上）第三次月考數(shù)學試卷

一、單項選擇題：本題共8小題，每小題5分，共40分.在每小題給出的四個選項中，只有一項符合題目要求.

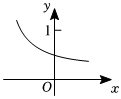• 1．若f（x）=a^x-b的圖像如圖，（a,b是常數(shù)），則（　　）

  A．a＞1，b＜0

  B．a＞1，b＞0

  C．0＜a＜1，b＞0

  D．0＜a＜1，b＜0
  組卷：527引用：3難度：0.7

  解析

• 2．已知函數(shù)f（x）=2^1-x+2^1+x，則（　　）

  A．f（x）是奇函數(shù)，且在（0，+∞）上單調遞增

  B．f（x）是奇函數(shù)，且在（0，+∞）上單調遞減

  C．f（x）是偶函數(shù)，且在（0，+∞）上單調遞增

  D．f（x）是偶函數(shù)，且在（0，+∞）上單調遞減
  組卷：58引用：2難度：0.8

  解析

• 3．設a,b∈R，則“a+b＞9”是“a＞5且b＞4”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充分必要條件	D．既不充分又不必要條件
  組卷：74引用：4難度：0.9

  解析

• 4．對三角函數(shù)線，下列說法正確的是（　　）

  A．對任意角都能作出正弦線、余弦線和正切線

  B．有的角的正弦線、余弦線和正切線都不存在

  C．任意角的正弦線、正切線總是存在的，但余弦線不一定存在

  D．任意角的正弦線、余弦線總是存在的，但正切線不一定存在
  組卷：52引用：3難度：0.9

  解析

• 5．在平面直角坐標系xOy中，P為直線3x+4y+1=0上一點．若向量

  a

  =（3，4），則向量

  OP

  在向量

  a

  上的投影向量為（　　）

  A．- 1 5	B．（- 3 5 ，- 4 5 ）
  C．（- 3 25 ，- 4 25 ）	D．無法確定
  組卷：61引用：1難度：0.8

  解析

• 6．已知函數(shù)f（x）=x³+x,g（x）=a^x+x（a＞1），h（x）=log_ax+x（a＞1）的零點分別為α，β，γ，則（　　）

  A．γ＜α＜β

  B．αβγ＜α

  C．β+γ＞α

  D．α+β+γ＜a-1
  組卷：46引用：1難度：0.5

  解析

• 7．已知全集U={-1，0，1，2，3}，集合A={0，1，2}，B={-1，0，2}，則（?_UA）∩B=（　　）

  A．{-1}

  B．{0，1}

  C．{-1，2，3}

  D．{-1，0，1，3}
  組卷：14引用：2難度：0.9

  解析

• 8．與

  y

  =

  x

  2

  |

  x

  |

  表示同一個函數(shù)的是（　　）

  A． y = x 2	B． y = （ x ） 2
  C． y = t , t ＞ 0 - t , t ＜ 0	D．y=|x|
  組卷：69引用：3難度：0.8

  解析

二、多項選擇題：本題共4小題，每小題5分，共20分，在每小題給出的四個選項中，有多

• 9．設函數(shù)y=f（x）的定義域為R，且滿足f（1+x）=f（1-x），f（x-2）+f（-x）=0，則下列說法正確的是（　　）

  A．y=f（x+1）是偶函數(shù)

  B．y=f（x+3）為奇函數(shù)

  C．f（x）是周期為4的周期函數(shù)

  D．f（1）=0
  組卷：96引用：7難度：0.5

  解析

• 10．已知函數(shù)f（x）=sin（x+φ）（0＜φ＜2π），g（x）=sin（ωx+

  π

  3

  ）（ω＞0），若把f（x）的圖象上每個點的橫坐標縮短為原來的

  1

  2

  倍后，再將圖象向右平移

  π

  6

  個單位，可以得到g（x），則下列說法正確的是（　　）

  A．φ= 2 3 π

  B．g（x）的周期為π

  C．g（x）的一個單調遞增區(qū)間為（ 7 π 12 ， 7 π 6 ）

  D．g（x）= 1 2 在區(qū)間（a,b）上有5個不同的解，則b-a的取值范圍為（2π，3π]
  組卷：76引用：5難度：0.6

  解析

• 11．下列各式正確的是（　　）

  A． （ - 3 ） 2 = - 3

  B． 4 a 4 = a

  C． （ 3 - 3 ） 3 = - 3

  D． 3 （ - 3 ） 3 = - 3
  組卷：45引用：1難度：0.8

  解析

• 12．下列說法不正確的是（　　）

  A．不等式（2x-1）（1-x）＜0的解集為 { x | 1 2 ＜ x ＜ 1 }

  B．若實數(shù)a,b,c滿足ac2＞bc2，則a＞b

  C．若x∈R，則函數(shù) y = x 2 + 4 + 1 x 2 + 4 的最小值為2

  D．當x∈R時，不等式kx2-kx+1＞0恒成立，則k的取值范圍是（0，4）
  組卷：348引用：16難度：0.6

  解析

三、填空題：本大題共4小題，每題5分，共20分.

• 13．已知f（x）=2sin（2x+

  π

  3

  ），若?x₁，x₂，x₃∈[0，

  3

  π

  2

  ]，使得f（x₁）=f（x₂）=f（x₃），若x₁+x₂+x₃的最大值為M，最小值為N，則M+N=

  ．
  組卷：488引用：13難度：0.5

  解析

• 14．已知lga+lgb=2，則ab的值為

  ．
  組卷：85引用：1難度：0.8

  解析

• 15．已知F（x）=

  x + ln （ - x ） - a , x ＜ 0

  e x x ， x ＞ 0

  圖象上存在關于原點對稱的點，則a的取值范圍是

  ．
  組卷：3引用：0難度：0.4

  解析

• 16．在平行四邊形ABCD中，E和F分別是CD和BC的中點，若

  AC

  =

  λ

  AE

  +

  μ

  AF

  ，其中λ，μ∈R，則

  1

  λ

  +

  1

  μ

  =

  ．
  組卷：23引用：1難度：0.7

  解析

四、解答題：本大題共6小題，共70分.解答應寫出文字說明、證明過程或演算步驟.

• 17．已知：集合A={x|3＜x≤6}，B={x|m≤x≤2m+1}．
  （1）若m=2，求A∩B；
  （2）若x∈A是x∈B的充分條件，求實數(shù)m的取值范圍；
  （3）若A∩B=?，求實數(shù)m的取值范圍．
  組卷：191引用：7難度：0.6

  解析

• 18．已知函數(shù)

  f

  （

  x

  ）

  =

  lo

  g

  2

  （

  x

  -

  6

  ）

  +

  lo

  g

  1

  2

  （

  a

  -

  x

  ）

  ，且f（8）=-1．
  （1）求f（x）的定義域；
  （2）求不等式f（2x-1）≥-1的解集．
  組卷：32引用：4難度：0.6

  解析

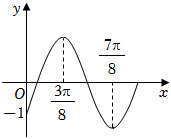• 19．已知函數(shù)f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤

  π

  2

  ）的部分圖象如圖所示．
  （1）求函數(shù)f（x）的解析式和單調增區(qū)間；
  （2）將函數(shù)f（x）的圖象向左平移

  π

  4

  個單位，再將圖象上各點的橫坐標伸長到原來的2倍（縱坐標不變）得到函數(shù)g（x）的圖象，若關于x的方程g（x）-2m=0在區(qū)間[0，π]上有兩個不同的解x₁，x₂，求g（

  x

  1

  +

  x

  2

  2

  ）的值及實數(shù)m的取值范圍．
  組卷：164引用：3難度：0.6

  解析

• 20．已知函數(shù)f（x）=（log₂x）²+alog₂x+3（a∈R）．
  （1）若a=1，求函數(shù)f（x）在區(qū)間

  [

  1

  2

  ，

  4

  ]

  上的值域；
  （2）若函數(shù)g（x）=f（x）+a在[1，8]上有零點，求實數(shù)a的取值范圍．
  組卷：457引用：1難度：0.5

  解析

• 21．求下列各式的值．
  （1）tan（-945°）；
  （2）7cos270°+3sin270°+tan765°．
  組卷：3引用：0難度：0.7

  解析

• 22．如圖，在海岸線EF一側有一休閑游樂場，游樂場的前一部分邊界為曲線段FGBC，該曲線段是函數(shù)y=Asin（ωx+φ）（A＞0，ω＞0，φ∈（0，π）），x∈[-4，0]的圖象，圖象的最高點為B（-1，2）．邊界的中間部分為長1千米的直線段CD，且CD∥EF．游樂場的后一部分邊界是以O為圓心的一段圓弧

  ?

  DE

  ．
  （1）求曲線段FGBC的函數(shù)表達式；
  （2）曲線段FGBC上的入口G距海岸線EF最近距離為1千米，現(xiàn)準備從入口G修一條筆直的景觀路到O，求景觀路GO長；
  （3）如圖，在扇形ODE區(qū)域內建一個平行四邊形休閑區(qū)OMPQ，平行四邊形的一邊在海岸線EF上，一邊在半徑OD上，另外一個頂點P在圓弧

  ?

  DE

  上，且∠POE=θ，求平行四邊形休閑區(qū)OMPQ面積的最大值及此時θ的值．
  組卷：332引用：6難度：0.5

  解析