當(dāng)前位置：試卷中心 > 試卷詳情

人教A版（2019）選擇性必修第一冊《第三章圓錐曲線的方程》2020年單元測試卷（3）

發(fā)布：2025/11/11 10:0:26

一、單選題

1．已知直線mx-y+1-2m=0恒過定點A，拋物線E：y²=2px（p＞0）的焦點坐標(biāo)為F（1，0），P為拋物線E上的動點，則|PA|+|PF|的最小值為（　　）
A．1 B．2 C．3 D．4
組卷：105引用：1難度：0.5
2．人們在進(jìn)行工業(yè)設(shè)計時，巧妙地利用了圓錐曲線的光學(xué)性質(zhì)．從雙曲線右焦點F₂發(fā)出的光線通過雙曲線鏡面反射出發(fā)散光線，且反射光線的反向延長線經(jīng)過左焦點F₁.已知雙曲線的方程為x²-y²=1，則當(dāng)入射光線F₂P和反射光線PE互相垂直時（其中P為入射點），∠F₁F₂P的余弦值大小為（　　）
A．
1
2
B．
2
2
C．
3
2
D．
6
-
2
4
組卷：57引用：3難度：0.6
3．已知F₁，F(xiàn)₂分別為雙曲線
x
2
4
-
y
2
5
=1的左、右焦點，M為雙曲線右支上一點，滿足MF₁⊥MF₂，則△F₁MF₂的面積為（　　）
A．5 B．10 C．
14
D．2
14
組卷：191引用：2難度：0.7
4．雙曲線C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的兩條漸近線與圓x²+y²-2x+
1
5
=0相切，則雙曲線C的離心率為（　　）
A．
5
2
B．
2
C．
5
D．
17
2
組卷：103引用：3難度：0.6
5．拋物線的光學(xué)性質(zhì)是：從拋物線焦點出發(fā)的光線經(jīng)拋物線反射后，反射光線與拋物線對稱軸平行．已知F、A（3，2）分別為拋物線y²=2px（p＞0）的焦點和內(nèi)側(cè)一點，拋物線上存在點P使得|PF|+|PA|=5，則實數(shù)p的取值范圍是（　　）
A．
（
-
∞
，
2
3
）
B．（4，+∞） C．
[
2
3
，
4
]
D．
（
2
3
，
4
]
組卷：75引用：2難度：0.7
6．已知F為雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右焦點，A為雙曲線虛軸的一個端點，直線FA與雙曲線的一條漸近線在y軸左側(cè)的交點為B，若
FA
=（
2
-1）
AB
，則此雙曲線漸近線的夾角為（　　）
A．
π
2
B．
π
3
C．
π
4
D．
π
6
組卷：33引用：2難度：0.6
7．與三角形的一條邊以及另外兩條邊的延長線都相切的圓被稱為三角形的旁切圓，旁切圓的圓心被稱為三角形的旁心，每個三角形有三個旁心，如圖1所示，已知F₁，F(xiàn)₂是雙曲線
x
2
9
-
y
2
16
=
1
的左右焦點，P是雙曲線右支上一點，Q是△PF₁F₂的一個旁心，如圖2所示，直線PQ與x軸交于點M，則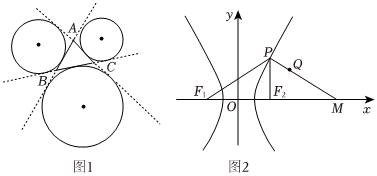
|
MQ
QP
|
=（　　）
A．
3
4
B．
4
3
C．
3
2
D．
5
3
組卷：85引用：4難度：0.5
8．已知點P在橢圓
x
2
8
+
y
2
2
=
1
上，F(xiàn)₁與F₂分別為左、右焦點，若
∠
F
1
P
F
2
=
2
π
3
，則△F₁PF₂的面積為（　　）
A．
2
3
B．
3
3
C．
4
3
D．
3
組卷：266引用：1難度：0.6

二、多選題

9．已知橢圓m²x²+4m²y²=1（m＞0），則下列說法正確的是（　　）
A．橢圓的焦點在x軸上 B．橢圓的焦點在y軸上
C．長軸長為
2
m
D．離心率為
3
2
組卷：16引用：1難度：0.7
10．已知橢圓
C
：
x
2
4
+
y
2
3
=
1
的左、右兩個焦點分別為F₁，F(xiàn)₂，P為橢圓上一動點，M（1，1），則下列結(jié)論正確的有（　　）
A．△PF₁F₂的周長為6 B．△PF₁F₂的最大面積為
3
C．存在點P使得
P
F
1
?
P
F
2
=
0
D．|PM|+|PF₁|的最大值為5
組卷：527引用：11難度：0.6
11．設(shè)橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，E（0，b），A（m,n）為橢圓E上一點，m≠0，點B，A關(guān)于x軸對稱，直線EA，EB分別與x軸交于M，N兩點，則（　　）
A．|AE|的最大值為
a
2
+
b
2
B．直線EA，EB的斜率乘積為定值
C．若y軸上存在點P，使得∠MPO=∠PNO，則P的坐標(biāo)為（0，a）或（0，-a）
D．直線AN過定點
組卷：106引用：3難度：0.5

12．古希臘著名數(shù)學(xué)家阿波羅尼斯發(fā)現(xiàn)：平面內(nèi)到兩個定點A，B的距離之比為定值λ（λ≠1）的點的軌跡是圓，此圓被稱為“阿波羅尼斯圓”．在平面直角坐標(biāo)系xOy中，已知A（-4，2），B（2，2），點P滿足
|
PA
|
|
PB
|
=
2
，設(shè)點P的軌跡為圓C，下列結(jié)論正確的是（　　）

A．圓C的方程是（x-4）²+（y-2）²=16

B．過點A向圓C引切線，兩條切線的夾角為

C．過點A作直線l,若圓C上恰有三個點到直線l距離為2，該直線斜率為

D．在直線y=2上存在異于A，B的兩點D，E，使得

組卷：320引用：19難度：0.5

三、填空題

13．已知雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F(xiàn)₂，點P在C的左支上，
|
P
F
2
|
=
3
a
，
|
P
F
1
+
P
F
2
|
=
2
b
，則C的離心率為
．
組卷：42引用：3難度：0.6
14．寫出一條過點A（1，2）且與拋物線C：y²=4x僅有一個公共點的直線方程：
．
組卷：44引用：1難度：0.8
15．若橢圓mx²+y²=1的一個焦點與拋物線y²=4x的焦點重合，則m=

．
組卷：207引用：2難度：0.7
16．已知雙曲線E：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的左、右焦點分別為F₁，F(xiàn)₂，過F₁的直線l：
3
x-y+m=0與雙曲線E的右支交于點M，O為坐標(biāo)原點，過點O作ON⊥MF₁，垂足為N，若
MN
=
5
NF
1
，則雙曲線E的離心率是
．
組卷：132引用：5難度：0.6

四、解答題

17．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的一個焦點為F（2，0），經(jīng)過點
（
0
，
2
）
，過焦點F的直線l與橢圓C交于A，B兩點，線段AB中點為D，O為坐標(biāo)原點，過O，D的直線交橢圓于M，N兩點．
（1）求橢圓C的方程；
（2）四邊形AMBN面積是否有最大值，若有求最大值，若沒有請說明理由．
組卷：152引用：3難度：0.4
18．歷史上第一個研究圓錐曲線的是梅納庫莫斯（公元前375年-325年），大約100年后，阿波羅尼斯更詳盡、系統(tǒng)地研究了圓錐曲線，并且他還進(jìn)一步研究了這些圓錐曲線的光學(xué)性質(zhì)：如圖甲，從橢圓的一個焦點出發(fā)的光線或聲波，經(jīng)橢圓反射后，反射光線經(jīng)過橢圓的另一個焦點，其中法線l′表示與橢圓C的切線垂直且過相應(yīng)切點的直線，利用橢圓的光學(xué)性質(zhì)解決以下問題：
如圖乙，橢圓C的中心在坐標(biāo)原點，焦點為F₁（-c,0），F(xiàn)₂（c,0）（c＞0），由F₁發(fā)出的光經(jīng)橢圓兩次反射后回到F₁經(jīng)過的路程為
8
3
3
c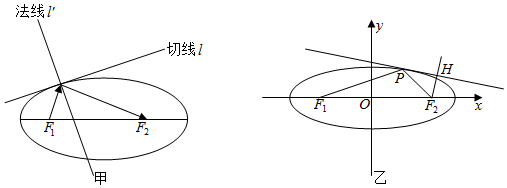
．
（1）求橢圓C的離心率；
（2）點P是橢圓C上除頂點外的任意一點，橢圓在點P處的切線為l,F₂在l上的射影H在圓x²+y²=4上，求橢圓C的方程．
組卷：152引用：1難度：0.5
19．已知平面內(nèi)動點P與點A（-2，0），B（2，0）連線的斜率之積為-
3
4
．
（1）求動點P的軌跡E的方程；
（2）過點F（1，0）的直線與曲線E交于P，Q兩點，直線AP，AQ與直線x=4分別交于M，N兩點．求證：以MN為直徑的圓恒過定點．
組卷：130引用：2難度：0.4
20．已知拋物線C₁的頂點在原點，對稱軸為坐標(biāo)軸，且過（-1，1），
（
1
，
2
）
，（2，-2），（-1，-2）四點中的兩點．
（1）求拋物線C₁的方程；
（2）若直線l與拋物線C₁交于M，N兩點，與拋物線
C
2
：
y
2
=
4
x
交于P，Q兩點，M，P在第一象限，N，Q在第四象限，且
|
NQ
|
|
MP
|
=
2
，求
|
PQ
|
|
MN
|
的值．
組卷：54引用：2難度：0.5
21．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
經(jīng)過點P（1，
2
2
），且離心率e=
2
2
．
（1）求橢圓C的標(biāo)準(zhǔn)方程；
（2）若斜率為k且不過點P的直線l交C于A，B兩點，記直線PA，PB的斜率分別為k₁，k₂，且k₁+k₂=0，求直線l的斜率k.
組卷：87引用：5難度：0.6
22．已知橢圓的焦點坐標(biāo)是F₁（-1，0），F(xiàn)₂（1，0），M是橢圓上一點，且
|
M
F
1
|
+
|
M
F
2
|
=
2
5
．
（1）求此橢圓的標(biāo)準(zhǔn)方程；
（2）若直線y=x+m交橢圓于A，B兩點，且AB的中點為P（-1，n），求n的值．
組卷：3引用：0難度：0.5

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測評 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會員，資源免費下載

A．橢圓的焦點在x軸上	B．橢圓的焦點在y軸上
C．長軸長為 2 m	D．離心率為 3 2

A．△PF₁F₂的周長為6	B．△PF₁F₂的最大面積為 3
C．存在點P使得 P F 1 ? P F 2 = 0	D．\|PM\|+\|PF₁\|的最大值為5

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

人教A版（2019）選擇性必修第一冊《第三章 圓錐曲線的方程》2020年單元測試卷（3）

一、單選題

1．已知直線mx-y+1-2m=0恒過定點A，拋物線E：y2=2px（p＞0）的焦點坐標(biāo)為F（1，0），P為拋物線E上的動點，則|PA|+|PF|的最小值為（ ）

3．已知F1，F(xiàn)2分別為雙曲線x24-y25=1的左、右焦點，M為雙曲線右支上一點，滿足MF1⊥MF2，則△F1MF2的面積為（ ）

4．雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的兩條漸近線與圓x2+y2-2x+15=0相切，則雙曲線C的離心率為（ ）

6．已知F為雙曲線x2a2-y2b2=1（a＞0，b＞0）的右焦點，A為雙曲線虛軸的一個端點，直線FA與雙曲線的一條漸近線在y軸左側(cè)的交點為B，若FA=（2-1）AB，則此雙曲線漸近線的夾角為（ ）

8．已知點P在橢圓x28+y22=1上，F(xiàn)1與F2分別為左、右焦點，若∠F1PF2=2π3，則△F1PF2的面積為（ ）

二、多選題

9．已知橢圓m2x2+4m2y2=1（m＞0），則下列說法正確的是（ ）

10．已知橢圓C：x24+y23=1的左、右兩個焦點分別為F1，F(xiàn)2，P為橢圓上一動點，M（1，1），則下列結(jié)論正確的有（ ）

11．設(shè)橢圓C：x2a2+y2b2=1（a＞b＞0），E（0，b），A（m,n）為橢圓E上一點，m≠0，點B，A關(guān)于x軸對稱，直線EA，EB分別與x軸交于M，N兩點，則（ ）

三、填空題

13．已知雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左、右焦點分別為F1，F(xiàn)2，點P在C的左支上，|PF2|=3a，|PF1+PF2|=2b，則C的離心率為 ．

14．寫出一條過點A（1，2）且與拋物線C：y2=4x僅有一個公共點的直線方程：．

15．若橢圓mx2+y2=1的一個焦點與拋物線y2=4x的焦點重合，則m= ．

16．已知雙曲線E：x2a2-y2b2=1（a＞0，b＞0）的左、右焦點分別為F1，F(xiàn)2，過F1的直線l：3x-y+m=0與雙曲線E的右支交于點M，O為坐標(biāo)原點，過點O作ON⊥MF1，垂足為N，若MN=5NF1，則雙曲線E的離心率是 ．

四、解答題

19．已知平面內(nèi)動點P與點A（-2，0），B（2，0）連線的斜率之積為-34．（1）求動點P的軌跡E的方程；（2）過點F（1，0）的直線與曲線E交于P，Q兩點，直線AP，AQ與直線x=4分別交于M，N兩點．求證：以MN為直徑的圓恒過定點．

21．已知橢圓C：x2a2+y2b2=1（a＞b＞0）經(jīng)過點P（1，22），且離心率e=22．（1）求橢圓C的標(biāo)準(zhǔn)方程；（2）若斜率為k且不過點P的直線l交C于A，B兩點，記直線PA，PB的斜率分別為k1，k2，且k1+k2=0，求直線l的斜率k.

22．已知橢圓的焦點坐標(biāo)是F1（-1，0），F(xiàn)2（1，0），M是橢圓上一點，且|MF1|+|MF2|=25．（1）求此橢圓的標(biāo)準(zhǔn)方程；（2）若直線y=x+m交橢圓于A，B兩點，且AB的中點為P（-1，n），求n的值．

人教A版（2019）選擇性必修第一冊《第三章圓錐曲線的方程》2020年單元測試卷（3）

1．已知直線mx-y+1-2m=0恒過定點A，拋物線E：y²=2px（p＞0）的焦點坐標(biāo)為F（1，0），P為拋物線E上的動點，則|PA|+|PF|的最小值為（　　）

3．已知F₁，F(xiàn)₂分別為雙曲線
x
2
4
-
y
2
5
=1的左、右焦點，M為雙曲線右支上一點，滿足MF₁⊥MF₂，則△F₁MF₂的面積為（　　）

4．雙曲線C：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的兩條漸近線與圓x²+y²-2x+
1
5
=0相切，則雙曲線C的離心率為（　　）

6．已知F為雙曲線
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的右焦點，A為雙曲線虛軸的一個端點，直線FA與雙曲線的一條漸近線在y軸左側(cè)的交點為B，若
FA
=（
2
-1）
AB
，則此雙曲線漸近線的夾角為（　　）

8．已知點P在橢圓
x
2
8
+
y
2
2
=
1
上，F(xiàn)₁與F₂分別為左、右焦點，若
∠
F
1
P
F
2
=
2
π
3
，則△F₁PF₂的面積為（　　）

9．已知橢圓m²x²+4m²y²=1（m＞0），則下列說法正確的是（　　）

10．已知橢圓
C
：
x
2
4
+
y
2
3
=
1
的左、右兩個焦點分別為F₁，F(xiàn)₂，P為橢圓上一動點，M（1，1），則下列結(jié)論正確的有（　　）

11．設(shè)橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
，E（0，b），A（m,n）為橢圓E上一點，m≠0，點B，A關(guān)于x軸對稱，直線EA，EB分別與x軸交于M，N兩點，則（　　）

13．已知雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F(xiàn)₂，點P在C的左支上，
|
P
F
2
|
=
3
a
，
|
P
F
1
+
P
F
2
|
=
2
b
，則C的離心率為
．

14．寫出一條過點A（1，2）且與拋物線C：y²=4x僅有一個公共點的直線方程：
．

15．若橢圓mx²+y²=1的一個焦點與拋物線y²=4x的焦點重合，則m=

．

16．已知雙曲線E：
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）的左、右焦點分別為F₁，F(xiàn)₂，過F₁的直線l：
3
x-y+m=0與雙曲線E的右支交于點M，O為坐標(biāo)原點，過點O作ON⊥MF₁，垂足為N，若
MN
=
5
NF
1
，則雙曲線E的離心率是
．

22．已知橢圓的焦點坐標(biāo)是F₁（-1，0），F(xiàn)₂（1，0），M是橢圓上一點，且
|
M
F
1
|
+
|
M
F
2
|
=
2
5
．
（1）求此橢圓的標(biāo)準(zhǔn)方程；
（2）若直線y=x+m交橢圓于A，B兩點，且AB的中點為P（-1，n），求n的值．