當(dāng)前位置：試卷中心 > 試卷詳情

2023年河北省唐山市高考數(shù)學(xué)二模試卷

發(fā)布：2025/11/12 3:0:29

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

1．已知函數(shù)
f
（
x
）
=
x
e
x
-
a
和
g
（
x
）
=
lnx
x
+
b
有相同的極大值，則a+b=（　　）
A．2 B．0 C．-3 D．-1
組卷：110引用：3難度：0.6
2．若復(fù)數(shù)
z
=
i
1
+
i
（i為虛數(shù)單位），則|
z
|=（　　）
A．
1
2
B．
2
2
C．1 D．
2
組卷：219引用：10難度：0.8
3．已知函數(shù)f（x）=sin（ωx+φ）（ω＞0，|φ|≤
π
2
），x=-
π
8
是函數(shù)f（x）的一個(gè)零點(diǎn)，x=
π
8
是函數(shù)f（x）的一條對稱軸，若f（x）在區(qū)間（
π
5
，
π
4
）上單調(diào)，則ω的最大值是（　　）
A．14 B．16 C．18 D．20
組卷：337引用：5難度：0.6
4．橢圓E：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點(diǎn)分別為F₁，F(xiàn)₂，直線l過F₂與E交于A，B兩點(diǎn)，△ABF₁為直角三角形，且|AF₁|，|AB|，|BF₁|成等差數(shù)列，則E的離心率為（　　）
A．
1
2
B．
2
2
C．
3
2
D．
3
4
組卷：161引用：3難度：0.5
5．已知圓
C
1
：
（
x
-
1
）
2
+
y
2
=
1
，圓
C
2
：
（
x
-
a
）
2
+
（
y
-
b
）
2
=
4
，其中a,b∈R．若兩圓外切，則
b
-
3
a
+
3
的取值范圍為（　　）
A．
[
-
24
7
，
0
]
B．
[
-
12
5
，
0
]
C．
[
0
，
24
7
]
D．
[
0
，
12
5
]
組卷：58引用：3難度：0.5
6．我們把各個(gè)數(shù)位上的數(shù)字之和為8的三位數(shù)稱為“幸運(yùn)數(shù)”，例如“170，332，800”都是“幸運(yùn)數(shù)”．問“幸運(yùn)數(shù)”的個(gè)數(shù)共有（　　）
A．35個(gè) B．36個(gè) C．37個(gè) D．38個(gè)
組卷：43引用：1難度：0.7
7．已知集合A={1，2，4}，B={2，4，6}，則A∪B=（　　）
A．{1，2，4} B．{2，4}
C．{1，2，2，4，4，6} D．{1，2，4，6}
組卷：155引用：1難度：0.9
8．近日，2021中國最具幸福感城市調(diào)查推選活動(dòng)正式啟動(dòng)，在100個(gè)地級及以上候選城市名單中，徐州市入選．“幸福感指數(shù)”是指某個(gè)人主觀地評價(jià)他對自己目前生活狀態(tài)的滿意程度的指標(biāo)，常用區(qū)間[0，10]內(nèi)的一個(gè)數(shù)來表示，該數(shù)越接近10表示滿意度越高．現(xiàn)隨機(jī)抽取20位徐州市居民，他們的幸福感指數(shù)見如表，則這組數(shù)據(jù)的80百分位數(shù)是（　　）

3 3 4 5 5 6 6 6 7 7

7 7 8 8 8 8 9 9 10 10

A．7.7 B．8 C．8.5 D．9
組卷：87引用：2難度：0.9

二、選擇題：本題共4小題，每小題5分，共20分.在每小題給出的選項(xiàng)中，有多項(xiàng)符合題目要求，全部選對的得5分，部分選對的得2分，有選錯(cuò)的得0分。

9．已知函數(shù)f（x）的定義域?yàn)閇0，+∞），且滿足當(dāng)x∈[0，4）時(shí)，f（x）=2-|x-2|，當(dāng)x≥4時(shí)，f（x）=λf（x-4），λ為非零常數(shù)，則下列說法正確的是（　　）

A．當(dāng)λ=1時(shí)，f（2023）=1

B．當(dāng)λ＜0時(shí)，函數(shù)f（x）在[2020，2022）單調(diào)遞增

C．當(dāng)λ=2時(shí)，記函數(shù)

（

）

的圖象與函數(shù)f（x）的圖象在[0，16]上的m個(gè)交點(diǎn)為（x_i，y_i）（i=1，2，…，m），則

∑

（

）

D．當(dāng)λ＜-1時(shí)，函數(shù)f（x）在[0，8n]（n∈N^*）上的值域?yàn)閇2λ^2n-1，2λ^2n-2]

組卷：24引用：1難度：0.4

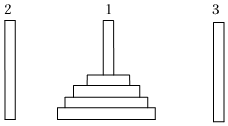10．著名的“河內(nèi)塔”問題中，地面直立著三根柱子，在1號(hào)柱上從上至下、從小到大套著n個(gè)中心帶孔的圓盤．將一個(gè)柱子最上方的一個(gè)圓盤移動(dòng)到另一個(gè)柱子，且保持每個(gè)柱子上較大的圓盤總在較小的圓盤下面，視為一次操作．設(shè)將n個(gè)圓盤全部從1號(hào)柱子移動(dòng)到3號(hào)柱子的最少操作數(shù)為a_n，則（　　）
A．a(chǎn)₂=3 B．a(chǎn)₃=8 C．a(chǎn)_n+1=2a_n+n D．
a
n
=
2
n
-
1
組卷：66引用：5難度：0.7

11．在三棱錐P-ABC中，AB=BC=2，AB⊥BC，設(shè)三棱錐P-ABC的體積為V，直線PB與平面ABC所成的角為α，則下列說法正確的是（　　）

A．若PA+PC=

，則V的最大值為

B．若PA+PC=

，則α的最大值為30°

C．若直線PA，PC與平面ABC所成的角分別為30°，60°，則α不可能為90°

D．若直線PA，PC與平面ABC所成的角分別為30°，60°，則V的最小值為

組卷：24引用：2難度：0.5

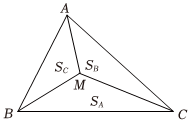12．“奔馳定理”因其幾何表示酷似奔馳的標(biāo)志得來，是平面向量中一個(gè)非常優(yōu)美的結(jié)論．奔馳定理與三角形四心（重心、內(nèi)心、外心、垂心）有著神秘的關(guān)聯(lián)．它的具體內(nèi)容是：已知M是△ABC內(nèi)一點(diǎn)，△BMC，△AMC，△AMB的面積分別為S_A，S_B，S_C，且
S
A
?
MA
+
S
B
?
MB
+
S
c
?
MC
=
0
．以下命題正確的有（　　）

A．若S_A：S_B：S_C=1：1：1，則M為△ABC的重心

B．若M為△ABC的內(nèi)心，則

C．若∠BAC=45°，∠ABC=60°，M為△ABC的外心，則

：

D．若M為△ABC的垂心，

，則

cos

∠

AMB

組卷：982引用：24難度：0.5

三、填空題：本題共4小題，每小題5分，共20分.

13．在棱長為2的正方體ABCD-A₁B₁C₁D₁中，若E為棱BB₁的中點(diǎn)，則平面AEC₁截正方體ABCD-A₁B₁C₁D₁的截面面積為
．
組卷：47引用：3難度：0.6
14．已知方程
x
2
2
m
-
1
-
y
2
m
+
2
=1表示雙曲線，則m的取值范圍是
．
組卷：30引用：3難度：0.7
15．已知x＞0，y＞0，且
lnx
=
e
x
y
-
lny
，則y-x+lnx的最小值為
．
組卷：2引用：0難度：0.3
16．某產(chǎn)品的廣告費(fèi)用x與銷售額y的統(tǒng)計(jì)數(shù)據(jù)如表
廣告費(fèi)用 x（萬元） 4 2 3 5
銷售額y（萬元） 49 26 39 54
根據(jù)上表可得回歸方程
?
y
=
?
b
x+
?
a
中的
?
b
為10，據(jù)此模型預(yù)報(bào)廣告費(fèi)用為6萬元時(shí)銷售額為

萬元．
組卷：77引用：3難度：0.7

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

17．已知數(shù)列{a_n}中，a₁=1，a_n+1=2a_n+1（n∈N*）．
（1）求a_n的通項(xiàng)公式；
（2）設(shè)b_n=（a_n+1）log₂（a_n+1）．求{b_n}的前n項(xiàng)和：
組卷：188引用：2難度：0.5
18．已知函數(shù)f（x）=x²+alnx.
（Ⅰ）當(dāng)a=-2時(shí)，求函數(shù)f（x）的單調(diào)區(qū)間和極值；
（Ⅱ）若g（x）=f（x）+
2
x
在[1，+∞）上是單調(diào)增函數(shù)，求實(shí)數(shù)a的取值范圍．
組卷：162引用：14難度：0.3
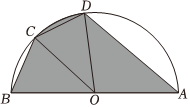19．如圖，有一景區(qū)的平面圖是一半圓形，其中AB長為2km,C、D兩點(diǎn)在半圓弧上，滿足BC=CD，設(shè)∠COB=θ．
（1）現(xiàn)要在景區(qū)內(nèi)鋪設(shè)一條觀光道路，由線段AB、BC、CD和DA組成，則當(dāng)θ為何值時(shí)，觀光道路的總長l最長，并求l的最大值；
（2）若要在景區(qū)內(nèi)種植鮮花，其中在△AOD和△BOC內(nèi)種滿鮮花，在扇形COD內(nèi)種一半面積的鮮花，則當(dāng)θ為何值時(shí)，鮮花種植面積S最大．
組卷：170引用：5難度：0.5
20．已知拋物線C：y²=2px,點(diǎn)A（1，2）在C上，A關(guān)于動(dòng)點(diǎn)T（t,0）（t＜3）的對稱點(diǎn)記為M，過M的直線l與C交于P（x₁，y₁），Q（x₂，y₂），M為P，Q的中點(diǎn)．
（1）當(dāng)直線l過坐標(biāo)原點(diǎn)O時(shí)，求△APQ外接圓的標(biāo)準(zhǔn)方程；
（2）求△APQ面積的最大值．
組卷：79引用：3難度：0.3
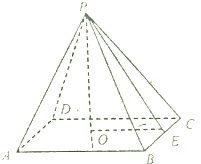21．已知正四棱錐P-ABCD中，AB=6cm,側(cè)面與底面ABCD所成角的大小為45°
（1）求正四棱錐的體積；
（2）側(cè)棱與底面所成角的大小（精確到1度）
組卷：3引用：0難度：0.9
22．某學(xué)校為了研究期中考試前學(xué)生所做數(shù)學(xué)模擬試題的套數(shù)與考試成績的關(guān)系，統(tǒng)計(jì)了五個(gè)班做的模擬試卷套數(shù)量及期中考試的平均分如下：

套（x） 7 6 6 5 6

數(shù)學(xué)平均分（y） 125 120 110 100 115

（1）若x與y成線性相關(guān)，則某班做了8套模擬試題，預(yù)計(jì)平均分為多少分？
（2）期中考試對學(xué)生進(jìn)行獎(jiǎng)勵(lì)，考入年級前200名，獲一等獎(jiǎng)學(xué)金500元；考入年級201-500名，獲二等獎(jiǎng)學(xué)金300元；考入年級501名以后的學(xué)生將不能獲得獎(jiǎng)學(xué)金．甲、乙兩名學(xué)生獲一等獎(jiǎng)學(xué)金的概率均為
2
5
，獲二等獎(jiǎng)學(xué)金的概率均為
1
3
，若甲、乙兩名學(xué)生獲得每個(gè)等級的獎(jiǎng)學(xué)金是相互獨(dú)立的，求甲、乙兩名學(xué)生所獲得獎(jiǎng)學(xué)金總金額X的分布列及數(shù)學(xué)期望．
附：
?
b
=
n
∑
i
=
1
（
x
i
-
x
）
（
y
i
-
y
）
n
∑
i
=
1
（
x
i
-
x
）
2
，
?
a
=
y
-
?
b
x
．
組卷：2引用：1難度：0.6

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測評 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會(huì)員，資源免費(fèi)下載

A．{1，2，4}	B．{2，4}
C．{1，2，2，4，4，6}	D．{1，2，4，6}

廣告費(fèi)用 x（萬元）	4	2	3	5
銷售額y（萬元）	49	26	39	54

套（x）	7	6	6	5	6
數(shù)學(xué)平均分（y）	125	120	110	100	115

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2023年河北省唐山市高考數(shù)學(xué)二模試卷

一、選擇題：本題共8小題，每小題5分，共40分。在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的。

1．已知函數(shù)f（x）=xex-a和g（x）=lnxx+b有相同的極大值，則a+b=（ ）

2．若復(fù)數(shù)z=i1+i（i為虛數(shù)單位），則|z|=（ ）

3．已知函數(shù)f（x）=sin（ωx+φ）（ω＞0，|φ|≤π2），x=-π8是函數(shù)f（x）的一個(gè)零點(diǎn)，x=π8是函數(shù)f（x）的一條對稱軸，若f（x）在區(qū)間（π5，π4）上單調(diào)，則ω的最大值是（ ）

4．橢圓E：x2a2+y2b2=1（a＞b＞0）的左、右焦點(diǎn)分別為F1，F(xiàn)2，直線l過F2與E交于A，B兩點(diǎn)，△ABF1為直角三角形，且|AF1|，|AB|，|BF1|成等差數(shù)列，則E的離心率為（ ）

5．已知圓C1：（x-1）2+y2=1，圓C2：（x-a）2+（y-b）2=4，其中a,b∈R．若兩圓外切，則b-3a+3的取值范圍為（ ）

6．我們把各個(gè)數(shù)位上的數(shù)字之和為8的三位數(shù)稱為“幸運(yùn)數(shù)”，例如“170，332，800”都是“幸運(yùn)數(shù)”．問“幸運(yùn)數(shù)”的個(gè)數(shù)共有（ ）

7．已知集合A={1，2，4}，B={2，4，6}，則A∪B=（ ）

二、選擇題：本題共4小題，每小題5分，共20分.在每小題給出的選項(xiàng)中，有多項(xiàng)符合題目要求，全部選對的得5分，部分選對的得2分，有選錯(cuò)的得0分。

9．已知函數(shù)f（x）的定義域?yàn)閇0，+∞），且滿足當(dāng)x∈[0，4）時(shí)，f（x）=2-|x-2|，當(dāng)x≥4時(shí)，f（x）=λf（x-4），λ為非零常數(shù)，則下列說法正確的是（ ）

11．在三棱錐P-ABC中，AB=BC=2，AB⊥BC，設(shè)三棱錐P-ABC的體積為V，直線PB與平面ABC所成的角為α，則下列說法正確的是（ ）

三、填空題：本題共4小題，每小題5分，共20分.

13．在棱長為2的正方體ABCD-A1B1C1D1中，若E為棱BB1的中點(diǎn)，則平面AEC1截正方體ABCD-A1B1C1D1的截面面積為 ．

14．已知方程x22m-1-y2m+2=1表示雙曲線，則m的取值范圍是．

15．已知x＞0，y＞0，且lnx=exy-lny，則y-x+lnx的最小值為 ．

四、解答題：本題共6小題，共70分.解答應(yīng)寫出文字說明、證明過程或演算步驟.

17．已知數(shù)列{an}中，a1=1，an+1=2an+1（n∈N*）．（1）求an的通項(xiàng)公式；（2）設(shè)bn=（an+1）log2（an+1）．求{bn}的前n項(xiàng)和：

18．已知函數(shù)f（x）=x2+alnx.（Ⅰ）當(dāng)a=-2時(shí)，求函數(shù)f（x）的單調(diào)區(qū)間和極值；（Ⅱ）若g（x）=f（x）+2x在[1，+∞）上是單調(diào)增函數(shù)，求實(shí)數(shù)a的取值范圍．

21．已知正四棱錐P-ABCD中，AB=6cm,側(cè)面與底面ABCD所成角的大小為45°（1）求正四棱錐的體積；（2）側(cè)棱與底面所成角的大小（精確到1度）

1．已知函數(shù)
f
（
x
）
=
x
e
x
-
a
和
g
（
x
）
=
lnx
x
+
b
有相同的極大值，則a+b=（　　）

2．若復(fù)數(shù)
z
=
i
1
+
i
（i為虛數(shù)單位），則|
z
|=（　　）

3．已知函數(shù)f（x）=sin（ωx+φ）（ω＞0，|φ|≤
π
2
），x=-
π
8
是函數(shù)f（x）的一個(gè)零點(diǎn)，x=
π
8
是函數(shù)f（x）的一條對稱軸，若f（x）在區(qū)間（
π
5
，
π
4
）上單調(diào)，則ω的最大值是（　　）

4．橢圓E：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的左、右焦點(diǎn)分別為F₁，F(xiàn)₂，直線l過F₂與E交于A，B兩點(diǎn)，△ABF₁為直角三角形，且|AF₁|，|AB|，|BF₁|成等差數(shù)列，則E的離心率為（　　）

5．已知圓
C
1
：
（
x
-
1
）
2
+
y
2
=
1
，圓
C
2
：
（
x
-
a
）
2
+
（
y
-
b
）
2
=
4
，其中a,b∈R．若兩圓外切，則
b
-
3
a
+
3
的取值范圍為（　　）

6．我們把各個(gè)數(shù)位上的數(shù)字之和為8的三位數(shù)稱為“幸運(yùn)數(shù)”，例如“170，332，800”都是“幸運(yùn)數(shù)”．問“幸運(yùn)數(shù)”的個(gè)數(shù)共有（　　）

7．已知集合A={1，2，4}，B={2，4，6}，則A∪B=（　　）

9．已知函數(shù)f（x）的定義域?yàn)閇0，+∞），且滿足當(dāng)x∈[0，4）時(shí)，f（x）=2-|x-2|，當(dāng)x≥4時(shí)，f（x）=λf（x-4），λ為非零常數(shù)，則下列說法正確的是（　　）

11．在三棱錐P-ABC中，AB=BC=2，AB⊥BC，設(shè)三棱錐P-ABC的體積為V，直線PB與平面ABC所成的角為α，則下列說法正確的是（　　）

13．在棱長為2的正方體ABCD-A₁B₁C₁D₁中，若E為棱BB₁的中點(diǎn)，則平面AEC₁截正方體ABCD-A₁B₁C₁D₁的截面面積為
．

14．已知方程
x
2
2
m
-
1
-
y
2
m
+
2
=1表示雙曲線，則m的取值范圍是
．

15．已知x＞0，y＞0，且
lnx
=
e
x
y
-
lny
，則y-x+lnx的最小值為
．

17．已知數(shù)列{a_n}中，a₁=1，a_n+1=2a_n+1（n∈N*）．
（1）求a_n的通項(xiàng)公式；
（2）設(shè)b_n=（a_n+1）log₂（a_n+1）．求{b_n}的前n項(xiàng)和：

18．已知函數(shù)f（x）=x²+alnx.
（Ⅰ）當(dāng)a=-2時(shí)，求函數(shù)f（x）的單調(diào)區(qū)間和極值；
（Ⅱ）若g（x）=f（x）+
2
x
在[1，+∞）上是單調(diào)增函數(shù)，求實(shí)數(shù)a的取值范圍．

21．已知正四棱錐P-ABCD中，AB=6cm,側(cè)面與底面ABCD所成角的大小為45°
（1）求正四棱錐的體積；
（2）側(cè)棱與底面所成角的大小（精確到1度）