2020年北京市延慶區(qū)高考數(shù)學(xué)一模試卷

一、選擇題共10小題，每小題4分，共40分．在每小題列出的四個選項中，選出符合題目要求的一項．

• 1．已知點P（1，-2）是角α終邊上一點，則sinα+cosα=（　　）

  A． 5 5

  B． 3 5 5

  C． - 3 5 5

  D． - 5 5
  組卷：319引用：7難度：0.7

  解析

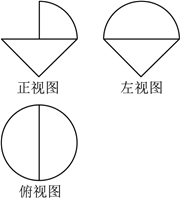• 2．某幾何體的三視圖如圖所示，其中正、側(cè)視圖中的三角形是斜邊為2的等腰直角三角形，則該幾何體的體積為（　　）

  A． 2 π 3

  B．π

  C． 8 π 3

  D．4π
  組卷：8引用：2難度：0.7

  解析

• 3．已知雙曲線

  C

  1

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  的右焦點F是拋物線

  C

  2

  ：

  y

  2

  =

  2

  px

  （

  p

  ＞

  0

  ）

  的焦點，且它們的公共弦過點F，則雙曲線C₁的離心率為（　　）

  A． 2

  B． 2 + 1

  C． 3

  D． 3 + 1
  組卷：56引用：4難度：0.6

  解析

• 4．復(fù)數(shù)z=1-i的虛部是（　　）

  A．1

  B．-1

  C．i

  D．-i
  組卷：178引用：14難度：0.9

  解析

• 5．下列函數(shù)中最小正周期為π的是（　　）
  ①f（x）=cosx?sinx；
  ②f（x）=cosx+sinx；
  ③

  f

  （

  x

  ）

  =

  sinx

  cosx

  ；
  ④f（x）=2sin²x

  A．①②

  B．②④

  C．①③④

  D．①②④
  組卷：208引用：3難度：0.8

  解析

• 6．已知a₁，a₂，b₁，b₂均為非零實數(shù)，不等式a₁x+b₁＜0與不等式a₂x+b₂＜0的解集分別為集合M和集合N，那么“

  a

  1

  a

  2

  =

  b

  1

  b

  2

  ”是“M=N”的（　　）

  A．充分非必要條件	B．既非充分又非必要條件
  C．充要條件	D．必要非充分條件
  組卷：106引用：3難度：0.9

  解析

• 7．設(shè)向量

  a

  =（cosx,-sinx），

  b

  =（-cos（

  π

  2

  -x），cosx），且

  a

  =t

  b

  ，t≠0，則sin2x的值等于（　　）

  A．1

  B．-1

  C．±1

  D．0
  組卷：424引用：8難度：0.7

  解析

• 8．中國的5G技術(shù)領(lǐng)先世界，5G技術(shù)的數(shù)學(xué)原理之一便是著名的香農(nóng)公式：C=Wlog₂（1+

  S

  N

  ）．它表示：在受噪聲干擾的信道中，最大信息傳遞速度C取決于信道帶寬W，信道內(nèi)信號的平均功率S，信道內(nèi)部的高斯噪聲功率N的大小，其中

  S

  N

  叫作信噪比．當(dāng)信噪比比較大時，公式中真數(shù)中的1可以忽略不計．按照香農(nóng)公式，若不改變帶寬W，而將信噪比

  S

  N

  從1000提升到8000，則C大約增加了（其中l(wèi)g5≈0.7）（　　）

  A．10%

  B．20%

  C．30%

  D．50%
  組卷：57引用：1難度：0.7

  解析

• 9．若偶函數(shù)f（x）在（-∞，0]上是增函數(shù)，則下列關(guān)系式中成立的是（　　）

  A．f（- 3 2 ）＜f（-1）＜f（2）	B．f（2）＜f（-1）＜f（- 3 2 ）
  C．f（2）＜f（- 3 2 ）＜f（-1）	D．f（-1）＜f（- 3 2 ）＜f（2）
  組卷：42引用：3難度：0.9

  解析

• 10．在二項式

  （

  2

  x

  +

  1

  4

  x

  ）

  n

  的展開式中，前三項的系數(shù)成等差數(shù)列，則該二項式展開式中x^-2項的系數(shù)為（　　）

  A．1

  B．4

  C．8

  D．16
  組卷：135引用：3難度：0.9

  解析

二、填空題共5小題，每小題5分，共25分．

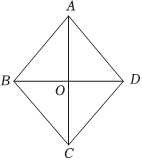• 11．菱形ABCD中，對角線AC=8，BD=6，則菱形的邊長為

  ．
  組卷：4引用：2難度：0.7

  解析

• 12．已知直線l經(jīng)過點A（-1，3），且與圓C：（x-1）²+y²=4相切，則直線l的方程為

  ．
  組卷：115引用：2難度：0.6

  解析

• 13．已知集合B和C，使得B∪C={1，2，3，4，5，6，7，8，9，10}，B∩C=?，并且C的元素乘積等于B的元素和，寫出所有滿足條件的集合C=

  ．
  組卷：231引用：1難度：0.3

  解析

• 14．若f（x）滿足f（x+1）=2x+3，則f（1）=

  ．
  組卷：20引用：3難度：0.8

  解析

• 15．二維碼是一種由黑色和白色組成的雙色方格陣圖，規(guī)定如果一個7×7的二維碼有對稱軸且繞其中心逆時針旋轉(zhuǎn)90°后能與自身重合，稱其為“轉(zhuǎn)轉(zhuǎn)碼”，則“轉(zhuǎn)轉(zhuǎn)碼”的個數(shù)為

  .（用數(shù)字作答）
  組卷：18引用：1難度：0.7

  解析

三、解答題共6小題，共85分．解答應(yīng)寫出文字說明，演算步驟或證明過程．

• 16．設(shè)數(shù)列{a_n}的前n項和為S_n，已知S_n=2a_n-n+1．
  （1）證明：數(shù)列{a_n+1}是等比數(shù)列；
  （2）若數(shù)列{b_n}滿足b₁=a₂，b_n+1=

  a n ， n 為奇數(shù) ，

  a n - b n ， n 為偶數(shù) ，

  求數(shù)列{b_n}的前14項的和．
  組卷：278引用：1難度：0.5

  解析

• 17．已知函數(shù)

  f

  （

  x

  ）

  =

  1

  x

  2

  ，g（x）=lnx.
  （1）若F（x）=mf（x）+2g（x）（m∈R）存在極值，求m的取值范圍．
  （2）若關(guān)于x的不等式af（x）+g（x）≥a在區(qū)間（0，1]上恒成立，求實數(shù)a的取值范圍．
  組卷：45引用：7難度：0.5

  解析

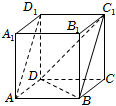• 18．已知正方體ABCD-A₁B₁C₁D₁．
  （1）證明：D₁A∥平面C₁BD；
  （2）求異面直線D₁A與BD所成的角．
  組卷：333引用：6難度：0.6

  解析

• 19．橢圓的光學(xué)性質(zhì)：光線從橢圓的一個焦點出發(fā)經(jīng)橢圓反射后通過另一個焦點．現(xiàn)有一橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  ，長軸A₁A₂長為4，從一個焦點F發(fā)出的一條光線經(jīng)橢圓內(nèi)壁上一點P反射之后恰好與x軸垂直，且

  PF

  =

  5

  2

  ．
  （1）求橢圓C的標(biāo)準(zhǔn)方程；
  （2）點Q為直線x=4上一點，且Q不在x軸上，直線QA₁，QA₂與橢圓C的另外一個交點分別為M，N，設(shè)△QA₁A₂，△QMN的面積分別為S₁，S₂，求

  S

  1

  S

  2

  的最大值．
  組卷：62引用：2難度：0.5

  解析

• 20．已知等差數(shù)列的前三項依次為a,4，3a,前n項和為S_n，且S_k=110．
  （1）求a及k的值．
  （2）已知數(shù)列{b_n}滿足

  b

  n

  =

  S

  n

  n

  ，證明數(shù)列{b_n}是等差數(shù)列，并求其前n項和T_n．
  組卷：778引用：8難度：0.6

  解析

• 21．甲乙兩人各有5個材質(zhì)、大小、形狀完全相同的小球，甲的小球上面標(biāo)有6，7，8，9，10五個數(shù)字，乙的小球上面標(biāo)有1，2，3，4，5五個數(shù)字．把各自的小球放入兩個不透明的口袋中，兩人同時從各自的口袋中隨機摸出1個小球．規(guī)定：若甲摸出的小球上的數(shù)字是乙摸出的小球上的數(shù)字的整數(shù)倍，則甲獲勝，否則乙獲勝．
  （1）寫出基本事件空間Ω；
  （2）你認(rèn)為“規(guī)定”對甲、乙二人公平嗎？說出你的理由．
  組卷：14引用：5難度：0.5

  解析