2025年山東省濟寧實驗中學高考數學一調試卷

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．在△ABC中，A=

  π

  4

  ，cosB=

  10

  10

  ，則sinC=（　　）

  A．- 5 5

  B． 5 5

  C．- 2 5 5

  D． 2 5 5
  組卷：349引用：5難度：0.8

  解析

• 2．下列函數在（0，+∞）上是增函數的是（　　）

  A． y = （ 1 3 ） x

  B．y=-2x+5

  C．y=lnx

  D．y= 3 x
  組卷：18引用：5難度：0.9

  解析

• 3．已知復數z=i（1-i），則其共軛復數

  z

  =（　　）

  A．-1-i

  B．-1+i

  C．1-i

  D．1+i
  組卷：202引用：8難度：0.8

  解析

• 4．已知

  C

  1011

  n

  =

  C

  1012

  n

  ，設（2x-3）ⁿ=a₀+a₁（x-1）+a₂（x-1）²+…+a_n（x-1）ⁿ，下列說法：
  ①n=2023，
  ②a_n=-3²⁰²³，
  ③a₀+a₁+a₂+…+a_n=1，
   ④展開式中所有項的二項式系數和為1．
  其中正確的個數有（　　）

  A．0

  B．1

  C．2

  D．3
  組卷：309引用：1難度：0.7

  解析

• 5．已知F為拋物線C：x²=8y的焦點，P為拋物線C上一點，點M的坐標為（-4，3），則△PMF周長的最小值是（　　）

  A． 5 + 15

  B． 5 + 17

  C．9

  D． 5 + 3 2
  組卷：308引用：6難度：0.5

  解析

• 6．一套游戲卡牌含紅色1點，紅色2點．…，紅色10點，及黑色1點，黑色2點，…，黑色10點，共計20張．現從中任意拽出兩張，記事件A，兩張卡片顏色不同，事件B：至少有一張卡片為偶數點，則P（A|B）=（　　）

  A． 3 4

  B． 10 19

  C． 19 28

  D． 15 29
  組卷：40引用：1難度：0.7

  解析

• 7．設x∈R，則“-2＜x＜2”是“1＜x＜2”的（　　）

  A．充分不必要條件	B．必要不充分條件
  C．充要條件	D．既不充分也不必要條件
  組卷：255引用：5難度：0.9

  解析

• 8．不等式x（x+1）＜2的解集是（　　）

  A．{x|-1＜x＜2}

  B．{x|-2＜x＜1}

  C．{x|x＜-1或x＞2}

  D．{x|x＜-2或x＞1}
  組卷：173引用：2難度：0.7

  解析

二、多項選擇題：本大題共3小題，每小題6分，共18分．在每小題給出的四個選項中，有多項符合題目要求，全部選對的得6分，部分選對得部分分，有選錯的得0分．

• 9．已知某果園的每棵果樹生長的果實個數為X，且X服從正態分布N（90，σ²），X小于70的概率為0.2，從該果園隨機選取10棵果樹，其中果實個數在[90，110]的果樹棵數記作隨機變量Y，則下列說法正確的是（　　）

  A．P（90≤X≤110）=0.3	B．P（Y=1）=0.3×0.79
  C．E（Y）=2	D．D（Y）=2.1
  組卷：72引用：2難度：0.8

  解析

• 10．下列結論正確的有（　　）

  A．若隨機變量ξ，η滿足η=2ξ+1，則D（η）=2D（ξ）+1

  B．若隨機變量ξ-N（3，σ2），且P（ξ＜6）=0.84，則P（3＜ξ＜6）=0.34

  C．若線性相關系數|r|越接近1，則兩個變量的線性相關性越強

  D．按從小到大順序排列的兩組數據：甲組：27，30，37，m,40，50；乙組：24，n,33，44，48，52，若這兩組數據的第30百分位數、第50百分位數都分別對應相等，則m+n=67
  組卷：94引用：4難度：0.7

  解析

• 11．下列各式化簡運算結果為1的是（　　）

  A．log53×log32×log25	B．lg 2 + 1 2 lg5
  C． lo g a a2（a＞0且a≠1）	D．eln3- （ 0 . 125 ） - 1 3
  組卷：302引用：5難度：0.8

  解析

三、填空題：本題共3小題，每小題5分，共15分

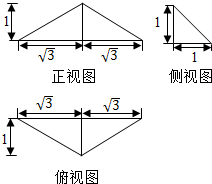• 12．已知某三棱錐的三視圖如圖所示，則該三棱錐的體積是

  ．
  組卷：1879引用：3難度：0.7

  解析

• 13．在△ABC中，G為△ABC的重心，

  S

  △

  ABC

  =

  9

  3

  ，

  cos

  ∠

  BAC

  =

  1

  2

  ，則

  GB

  ?

  GC

  的最大值為

  ．
  組卷：25引用：2難度：0.6

  解析

• 14．已知函數f（x）=m（lnx-x）（m∈R）的圖像與g（x）=x²-2lnx的圖像在區間

  [

  1

  e

  ，

  e

  ]

  上存在關于x軸對稱的點，則m的取值范圍是

  ．
  組卷：3引用：1難度：0.6

  解析

四、解答題：本題共5小題，共77分，解答應寫出文字說明、證明過程或演算步驟．

• 15．已知等差數列{a_n}的前四項和為10，且a₂，a₃，a₇成等比數列．
  （1）求數列{a_n}通項公式；
  （2）設

  b

  n

  =

  a

  n

  +

  2

  n

  ，求數列{b_n}的前n項和S_n．
  組卷：511引用：15難度：0.7

  解析

• 16．某年級對“熱愛籃球運動與性別是否有關”作了一次調查，被調查的男、女生人數均為4n（n∈N^*），其中男生熱愛籃球運動的人數占被調查男生人數的

  3

  4

  ，女生熱愛籃球運動的人數占被調查女生人數的

  1

  2

  ．若根據獨立性檢驗認為熱愛籃球運動與性別有關，且此推斷犯錯誤的概率超過0.01但不超過0.05．
  （1）求被調查的學生中男生人數的所有可能結果；
  （2）當被調查的學生人數取最小值時，現從被調查的熱愛籃球運動的學生中，用比例分配的分層隨機抽樣方法抽取10人參加某籃球賽事的志愿活動，再從這10人中任選4人擔任助理裁判．設4名助理裁判中女生人數為X，求X的分布列和均值．
  附：

  K

  2

  =

  n

  （

  ad

  -

  bc

  ）

  2

  （

  a

  +

  b

  ）

  （

  c

  +

  d

  ）

  （

  a

  +

  c

  ）

  （

  b

  +

  d

  ）

  ，其中n=a+b+c+d.
  

  α	0.1	0.05	0.01	0.005	0.001
  xα	2.706	3.841	6.635	7.879	10.828
  組卷：16引用：2難度：0.5

  解析

• 17．已知函數f（x）=x-alnx,

  g

  （

  x

  ）

  =

  -

  1

  +

  a

  x

  （

  a

  ＞

  0

  ）

  ．
  （1）若f（x）在點（1，f（1））處的切線為y=1，求實數a的值；
  （2）設函數h（x）=f（x）g（x），求函數h（x）的單調區間與極值；
  （3）若存在x₀∈[1，e]，使得f（x₀）＜g（x₀）成立，求a的取值范圍．
  組卷：70引用：2難度：0.2

  解析

• 18．已知函數f（x）=e^x-mx,其中e是自然常數．
  （1）討論函數f（x）的單調性；
  （2）若f（x）≥（a-m）x-sinx+1，對?x＞0恒成立，求實數a的取值范圍．
  組卷：38引用：1難度：0.5

  解析

• 19．已知雙曲線

  Γ

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  0

  ，

  b

  ＞

  0

  ）

  過點（4，13），離心率為

  14

  ，直線l：x=9交x軸于點A，過點A作直線交雙曲線Γ于M，N兩點．
  （Ⅰ）求雙曲線Γ的標準方程；
  （Ⅱ）若M是線段AN的中點，求直線MN的方程；
  （Ⅲ）設P，Q是直線l上關于x軸對稱的兩點，直線PM與QN的交點是否在一條直線上？請說明你的理由．
  組卷：124引用：1難度：0.3

  解析