蘇教版（2019）選擇性必修第一冊《3.1.1 橢圓的標準方程》2024年同步練習卷（1）（1）

一、選擇題

• 1．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1 （a＞b＞0）有兩個頂點在直線x

  +

  4

  3

  y=4上，則此橢圓的焦點坐標是（　　）

  A．（±5，0）

  B．（0，±5）

  C．（± 7 ，0）

  D．（0，± 7 ）
  組卷：21引用：1難度：0.9

  解析

• 2．若橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  過點

  M

  （

  1

  ，

  6

  3

  ）

  ，

  N

  （

  -

  3

  2

  ，

  1

  2

  ）

  ，則橢圓方程為（　　）

  A． x 2 3 + y 2 = 1

  B． x 2 4 + y 2 8 9 = 1

  C． x 2 2 + y 2 = 1

  D． x 2 + y 2 3 = 1
  組卷：332引用：1難度：0.8

  解析

• 3．平面內點P到F₁（-3，0）、F₂（3，0）的距離之和是10，則動點P的軌跡方程是（　　）

  A． x 2 25 + y 2 9 = 1	B． x 2 25 + y 2 16 = 1
  C． y 2 25 + x 2 9 = 1	D． y 2 25 + x 2 16 = 1
  組卷：105引用：19難度：0.7

  解析

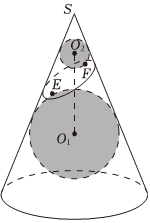• 4．如圖是數學家GerminalDandelin用來證明一個平面截圓錐得到的截口曲線是橢圓的模型（稱為“Dandelin雙球”）；在圓錐內放兩個大小不同的小球，使得它們分別與圓錐的側面、截面相切，設圖中球O₁，球O₂的半徑分別為4和1，球心距|O₁O₂|=6，截面分別與球O₁，球O₂切于點E，F，（E，F是截口橢圓的焦點），則此橢圓的離心率等于（　　）

  A． 33 9

  B． 6 3

  C． 2 2

  D． 1 6
  組卷：330引用：4難度：0.5

  解析

二、多選題

• 5．已知橢圓C：

  x

  2

  4

  +

  y

  2

  3

  =

  1

  的左、右焦點分別為F₁、F₂，P（x₀，y₀）為橢圓C上的一點，且在第一象限，點Q（m,n）為△PF₁F₂的內心，下列說法正確的是（　　）

  A．2y0=3n	B．|PF1|-|PF2|=2m
  C．x0=2m	D．m+n的最大值為 2 3 3
  組卷：339引用：3難度：0.5

  解析

• 6．已知橢圓

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  的一個焦點和一個頂點在直線y=2x-4上，則該橢圓的標準方程為（　　）

  A． x 2 20 + y 2 16 = 1	B． x 2 16 + y 2 4 = 1
  C． x 2 16 + y 2 20 = 1	D． x 2 4 + y 2 20 = 1
  組卷：33引用：5難度：0.7

  解析

• 7．點F₁，F₂為橢圓C的兩個焦點，若橢圓C上存在點P，使得∠F₁PF₂=90°，則橢圓C方程可以是（　　）

  A． x 2 25 + y 2 9 = 1	B． x 2 25 + y 2 16 = 1
  C． x 2 18 + y 2 9 = 1	D． x 2 16 + y 2 9 = 1
  組卷：130引用：6難度：0.6

  解析

三、填空題

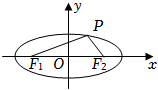• 8．如圖，橢圓

  x

  2

  a

  2

  +

  y

  2

  2

  =1的左、右焦點分別為F₁、F₂，點P在橢圓上，若|PF₁|=4，∠F₁PF₂=120°，則a的值為

  ．
  組卷：493引用：2難度：0.6

  解析

• 9．設F₁，F₂分別是橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =1（a＞b＞0）的左、右焦點，點P在橢圓上，且PF₁⊥PF₂，|PF₁|?|PF₂|=2，若a=2b,則橢圓的標準方程為

  ．
  組卷：421引用：4難度：0.8

  解析

• 10．M是圓C：x²+y²=1上的動點，點N（2，0），則線段MN的中點P的軌跡方程是

  ．
  組卷：12引用：3難度：0.5

  解析