2018年四川省綿陽市高考數學二診試卷(理科)
發布:2025/11/12 15:0:56
一、選擇題:本大題共12小題,每小題5分,共60分在每小題給出的四個選項中,只有一個是符合題目要求的.
-
1.若i為虛數單位,則復數
的實部為( )z=2-i1-i組卷:70引用:2難度:0.8解析 -
2.某校計劃選拔4名學生參加科技創新大賽.現從3名女生、5名男生中進行選擇,要求隊伍中至少包含男、女生各1名,則不同選法的總數為( )
組卷:55引用:1難度:0.7解析 -
3.
-(-10)0+(log2912)?(142)的值等于( )log2組卷:1018引用:8難度:0.9解析 -
4.F1,F2是雙曲線C:
的左、右焦點,過左焦點F1的直線l與雙曲線C的左、右兩支分別交于A、B兩點,若|AB|=|BF2|=|AF2|,則雙曲線的離心率為( )x2a2-y2b2=1(a>b,b>0)組卷:81引用:2難度:0.7解析 -
5.曲線y=lnx+x在點M(1,1)處的切線與坐標軸圍成三角形的面積是( )
組卷:14引用:9難度:0.7解析 -
6.已知拋物線C:y2=4x,直線l與拋物線C交于A,B兩點,線段AB的中點為(4,2),則l的方程為( )
組卷:125引用:2難度:0.7解析 -
7.集合A={x|-1<x<2},B={x|a<x<b},若“a=-2”是“A∩B≠?”的充分條件,則b的取值范圍是( )
組卷:92引用:1難度:0.7解析 -
8.已知函數f(x)=(x+m)ex-n(lnx+x)在x=1處的切線方程為y=(2e-2)x+1-e,不等式f(x)≥a恒成立,則a的最大值為( )
組卷:11引用:1難度:0.6解析 -
9.已知集合A={x|-1<2x<2,x∈R},集合B={x|-1<log2x<2,x∈R},則集合A∩B=( )
組卷:126引用:3難度:0.8解析 -
10.已知函數f(x)=sinxcos(2x+φ)(φ∈[0,π])為偶函數,則φ=( )
組卷:379引用:3難度:0.8解析 -
11.在區間(0,4]上隨機取值作為x,則x2+2x≥3-lnx的概率為( )
組卷:14引用:2難度:0.6解析 -
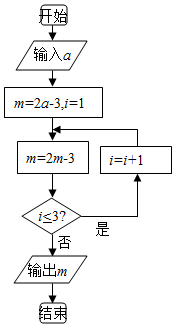 12.《算法統宗》是中國古代數學名著,由明代數學家程大位所著,該書完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉變,對我國民間普及珠算和數學知識起到了很大的作用.如圖所示的程序框圖的算法思路源于該書中的“李白沽酒”問題,執行該程序框圖,若輸入的a值為5,則輸出的值為( )組卷:18引用:2難度:0.8
12.《算法統宗》是中國古代數學名著,由明代數學家程大位所著,該書完善了珠算口訣,確立了算盤用法,完成了由籌算到珠算的徹底轉變,對我國民間普及珠算和數學知識起到了很大的作用.如圖所示的程序框圖的算法思路源于該書中的“李白沽酒”問題,執行該程序框圖,若輸入的a值為5,則輸出的值為( )組卷:18引用:2難度:0.8解析
二、填空題:本大題共4小題,每小題5分,共20分.
-
13.已知f(x)=(2x-3)n(n∈N*)展開式的二項式系數和為512,f(x)=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n.則a2=.
組卷:15引用:2難度:0.6解析 -
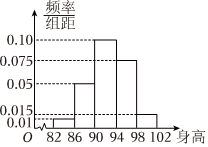 14.為了解某地兒童生長發育情況,抽查了100名3周歲女童的身高(cm),將統計結果繪制成頻率分布直方圖如圖,則可以估計這100名女童身高的平均值為 cm.組卷:42引用:2難度:0.7
14.為了解某地兒童生長發育情況,抽查了100名3周歲女童的身高(cm),將統計結果繪制成頻率分布直方圖如圖,則可以估計這100名女童身高的平均值為 cm.組卷:42引用:2難度:0.7解析 -
15.函數f(x)=4cos2
cos(x2-x)-2sinx-|ln(x+1)|的零點個數為 .π2組卷:2008引用:32難度:0.5解析 -
16.已知a,b為直線,α,β為平面,有下列三個命題:
①a∥α,b∥β,α∥β,則a∥b;
②a⊥α,b⊥α,則a∥b;
③a∥b,b?α,則a∥α;
④a⊥b,a⊥α,則b∥α.
其中正確命題是.組卷:8引用:1難度:0.7解析
三、解答題:本大題共5小題,共70分解答應寫出文字說明、證明過程或演算步驟.
-
17.2022年卡塔爾世界杯期間,甲、乙兩位同學參加學校組織的世界杯知識答題游戲,規則如下:甲同學先回答2道題,至少答對一道題后,乙同學才有機會答題,同樣也是兩次答題機會.兩位同學每答對一道題可獲得5積分,答錯不得分,甲同學每道題答對的概率均為
,乙同學每道題答對的概率均為23,每道題答對與否互不影響.12
(1)求乙同學有機會答題的概率;
(2)記X為甲和乙同學一共拿到的積分,求X的分布列和數學期望.組卷:25引用:2難度:0.5解析 -
18.在直角坐標系xOy中曲線C的參數方程為
(φ為參數,0≤φ≤π).x=1+cosφy=sinφ
(1)求曲線C的普通方程;
(2)直線y=kx+1與曲線C只有一個公共點,求k的取值范圍.組卷:5引用:1難度:0.5解析 -
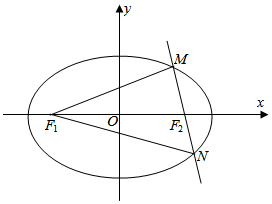 19.已知橢圓的焦點坐標為F1(-1,0),F2(1,0),過F2垂直于長軸的直線交橢圓于M、N兩點,且|MN|=3,
19.已知橢圓的焦點坐標為F1(-1,0),F2(1,0),過F2垂直于長軸的直線交橢圓于M、N兩點,且|MN|=3,
(1)求橢圓的方程;
(2)過F2的直線l與橢圓交于不同的兩點M、N,則△F1MN的內切圓的面積是否存在最大值?若存在求出這個最大值及此時的直線方程;若不存在,請說明理由.組卷:99引用:1難度:0.1解析 -
20.已知函數f(x)=x-alnx,g(x)=-
,其中a∈R1+ax
(1)設函數h(x)=f(x)-g(x),求函數h(x)的單調區間;
(2)若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范圍.組卷:228引用:8難度:0.1解析 -
21.將下列三角函數化為0°~45°角的三角函數.
(1)sin115°;
(2)cos105°;
(3)tan160°;
(4)sin85°.組卷:16引用:1難度:0.8解析
請考生在第22、23兩題中任選一題作答.注意:只能做所選定的題目.如果多做,則按所做的第一個題目計分,作答時請用2B鉛筆在答題卡,上將所選題號后的方框.[選修4-4:坐標系與參數方程]
-
22.(1)解不等式:x+|2x-1|<3
(2)求函數y=xlnx的導數.組卷:41引用:1難度:0.5解析
[選修4-5:不等式選講]
-
23.已知等差數列{an}中,a2=2,a1+a5=6.
(1)求{an}的通項公式;
(2)若,求數列{bn}的前n項和Sn.bn=2an組卷:327引用:12難度:0.7解析


