當(dāng)前位置：試卷中心 > 試卷詳情

2022年河南省湘豫名校高考數(shù)學(xué)聯(lián)考試卷（文科）（3月份）

發(fā)布：2025/11/12 15:0:56

一、選擇題：本題共12小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項符合題目要求．

1．命題“?x∈R，3x²+2x-5＜0”的否定是（　　）
A．?x∈R，3x²+2x-5＞0 B．?x∈R，3x²+2x-5≥0
C．?x∈R，3x²+2x-5＞0 D．?x∈R，3x²+2x-5≥0
組卷：19引用：8難度：0.8
2．平面直角坐標(biāo)系中，角α的終邊經(jīng)過點
P
（
1
，
3
）
，則
sin
（
π
2
-
α
）
=（　　）
A．
1
2
B．
3
2
C．
-
3
2
D．
-
1
2
組卷：477引用：5難度：0.8
3．已知等差數(shù)列{a_n}滿足a₁=2，S₅=S₁₂，若a_m+a₅=0，則m=（　　）
A．10 B．11 C．12 D．13
組卷：25引用：1難度：0.9
4．若實數(shù)x,y滿足約束條件
2
x
-
y
≤
0
x
-
1
≤
0
x
+
y
-
1
≥
0
，則z=y-x的最小值是（　　）
A．1 B．
1
3
C．
-
1
3
D．-1
組卷：83引用：6難度：0.8
5．若復(fù)數(shù)z滿足|z-1+i|=1，z在復(fù)平面內(nèi)對應(yīng)的點為（x,y），則（　　）
A．（x+1）²+（y+1）²=1 B．（x+1）²+（y-1）²=1
C．（x-1）²+（y-1）²=1 D．（x-1）²+（y+1）²=1
組卷：163引用：3難度：0.8
6．函數(shù)
f
（
x
）
=
2
x
2
-
1
（x∈[2，6]）的最大值為（　　）
A．2 B．
2
3
C．
2
5
D．
2
35
組卷：178引用：3難度：0.8
7．過點（0，3）且與曲線y=x³-2x+1相切的直線方程為（　　）
A．x-y-3=0 B．x-y+3=0 C．x+y+3=0 D．x+y-3=0
組卷：243引用：4難度：0.7
8．下列命題中，正確的是（　　）
A．
y
=
cos
（
3
2
π
+
θ
）
為偶函數(shù)
B．
y
=
sinx
（
1
-
sinx
）
1
-
sinx
為奇函數(shù)
C．
y
=
sin
2
x
sinx
-
1
為偶函數(shù)
D．
y
=
1
+
sinx
-
cosx
1
+
sinx
+
cosx
為奇函數(shù)
組卷：15引用：1難度：0.9
9．已知直線l過定點（0，1），則“直線l與圓（x-2）²+y²=4相切”是“直線l的斜率為
3
4
”的（　　）
A．充分不必要條件 B．必要不充分條件
C．充分必要條件 D．既不充分也不必要條件
組卷：81引用：3難度：0.9
10．如圖陰影部分為已曲邊梯形，其曲線對應(yīng)函數(shù)為y=e^x-1，在長方形內(nèi)隨機(jī)投擲一顆黃豆，則它落在陰影部分的概率是（　　）
A．
e
-
2
3
B．
e
-
1
3
C．
4
-
e
3
D．
5
-
e
3
組卷：29引用：3難度：0.7
11．已知集合A={x|x-1＞0}，B={x|x²-2x≤0}，則A∩B=（　　）
A．[0，2] B．[1，2） C．（1，2] D．[2，+∞）
組卷：248引用：7難度：0.8
12．函數(shù)f（x）=
xsin
（
π
2
+
x
）
e
|
x
|
的圖象大致為（　　）
A． B．
C． D．
組卷：87引用：3難度：0.7

二、填空題：本題共4小題，每小題5分，共20分．

13．最早發(fā)現(xiàn)勾股定理的人應(yīng)是我國商朝數(shù)學(xué)家商高，根據(jù)文獻(xiàn)記載，商高曾經(jīng)和周公討論過“勾三股四弦五”的問題，所以商高比畢達(dá)哥拉斯早500多年發(fā)現(xiàn)勾股定理．現(xiàn)有△ABC滿足“勾三股四弦五”，其中AB=4，D為弦BC上一點（不與B、C重合），且△ABD滿足“勾三股四弦五”，則
AB
?
AD
=
．
組卷：33引用：1難度：0.7
14．若將函數(shù)f（x）=sin（2x+φ）（0＜φ＜π）的圖象向右平移
π
3
個單位長度后得到的圖象對應(yīng)函數(shù)為奇函數(shù)，則φ=
．
組卷：347引用：9難度：0.5
15．某大學(xué)為了解在校本科生對參加某項社會實踐活動的意向，擬采用分層抽樣的方向，從該校四個年級的本科生中抽取一個容量為300的樣本進(jìn)行調(diào)查，已知該校一年級、二年級、三年級、四年級的本科生人數(shù)之比為4：5：5：6，則應(yīng)從一年級本科生中抽取
名學(xué)生．
組卷：1917引用：64難度：0.7
16．已知點P為雙曲線
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）右支上的一點，點F₁，F(xiàn)₂分別為雙曲線的左、右焦點，若M為△PF₁F₂的內(nèi)心，且S_△PMF₁=S_△PMF₂+
1
2
S
△
M
F
1
F
2
，則雙曲線的離心率為
．
組卷：236引用：3難度：0.6

三、解答題；共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟，第17～21題為必考題，每個試題考生都必須作答．第22、23題為選考題，考生根據(jù)要求作答．（一）必考題：共60分．

17．（1）已知a,b,c,d∈R求證：（a²+b²）（c²+d²）≥（ac+bd）²；
（2）?a,b,c＞0，a+b+c=3，求證：a²+b²+c²≥3．
組卷：12引用：2難度：0.5
18．已知函數(shù)f（x）=e^x-ln（x+m）．
（1）當(dāng)
m
=
1
2
時，求曲線f（x）在點（0，f（0））處切線方程；
（2）當(dāng)m≤2時，求證：f（x）＞0．
組卷：158引用：2難度：0.4
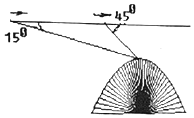19．航空測量組的飛機(jī)航線和山頂在同一鉛直平面內(nèi)，已知飛機(jī)的高度為海拔10千米，速度為180千米/小時．飛機(jī)先看到山頂?shù)母┙菫?5°，經(jīng)過420秒后又看到山頂?shù)母┙菫?5°，求山頂?shù)暮０胃叨龋ㄈ?div dealflag="1" class="MathJye" mathtag="math">
2
=
1
.
4
，
3
=
1
.
7
）．

組卷：18引用：3難度：0.5

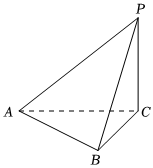20．如圖，在三棱錐P-ABC中，高PC=4（PC⊥底面ABC），AB=BC=3，∠ABC=120°．
（1）求三棱錐P-ABC的體積；
（2）求三棱錐P-ABC外接球的表面積．

組卷：195引用：1難度：0.6

21．已知橢圓C：
x
2
a
2
+
y
2
b
2
=
1
（a＞b＞0）的離心率為
1
2
，左、右焦點分別為F₁，F(xiàn)₂，點D在橢圓C上，△DF₁F₂的周長為6．
（1）求橢圓C的方程；
（2）已知直線l經(jīng)過點A（2，1）且斜率為k,與橢圓C交于不同的兩點M，N，若|OA|，|AM|，|AN|（O為坐標(biāo)原點）滿足|OA|²=4|AM|?|AN|，判斷k是否為定值？若是，請求出該定值；若不是，請說明理由．

組卷：39引用：1難度：0.5

[選修4-4：坐標(biāo)系與參數(shù)方程]（共1小題，滿分10分）

22．已知在直角坐標(biāo)系xOy中，直線l的參數(shù)方程是
x
=
2
+
tcosα
y
=
2
+
tsinα
，（t為參數(shù)），曲線C的參數(shù)方程是
x
=
2
cosφ
y
=
2
sinφ
，（φ為參數(shù)），點P（2，2）．
（Ⅰ）將曲線C的方程化為普通方程，并指出曲線C是哪一種曲線；
（Ⅱ）直線l與曲線C交于點A，B，當(dāng)|PA|+|PB|=4
2
時，求直線l的斜率．
組卷：42引用：2難度：0.8

[選修4-5：不等式選講]

23．直播帶貨業(yè)務(wù)是當(dāng)前行業(yè)電商的主要業(yè)務(wù)構(gòu)成之一．某公司通過抖音，快手，淘寶等直播平臺與網(wǎng)紅，明星等進(jìn)行帶貨合作，甲公司和乙公司所售商品存在競爭關(guān)系，兩公司在某購物平臺上同時開啟直播帶貨促銷活動．
（1）現(xiàn)對某時段21-40歲年齡段100名用戶觀看直播后選擇甲公司和乙公司所售商品選購情況進(jìn)行調(diào)查，統(tǒng)計數(shù)據(jù)如下表：

用戶年齡段選購甲公司選購乙公司合計

21-30歲 15 60

31-40歲 15 40

合計 100

請完成上述2×2列聯(lián)表，并判斷是否有99.9%的把握認(rèn)為選擇哪家直播間購物與用戶年?有關(guān)？
（2）五一期間，甲公司購物平臺直播間進(jìn)行“搶購”活動，假設(shè)直播間每人下單的概率均為p（0＜p＜1），直播間每人下單成功與否互不影響．若從直播間隨機(jī)抽取5人，記5人中恰有3人下單成功的概率為f（p），求f（p）的最大值，并求出取得最大值時p的值．
參考公式：
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，其中n=a+b+c+d.
臨界值表：

p（χ²≥x₀） 0.10 0.05 0.01 0.005 0.001

x₀ 2.706 3.841 6.635 7.879 10.828

組卷：57引用：2難度：0.7

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測評 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會員，資源免費(fèi)下載

A．?x∈R，3x²+2x-5＞0	B．?x∈R，3x²+2x-5≥0
C．?x∈R，3x²+2x-5＞0	D．?x∈R，3x²+2x-5≥0

A．（x+1）²+（y+1）²=1	B．（x+1）²+（y-1）²=1
C．（x-1）²+（y-1）²=1	D．（x-1）²+（y+1）²=1

A．充分不必要條件	B．必要不充分條件
C．充分必要條件	D．既不充分也不必要條件

用戶年齡段	選購甲公司	選購乙公司	合計
21-30歲	15		60
31-40歲		15	40
合計			100

p（χ²≥x₀）	0.10	0.05	0.01	0.005	0.001
x₀	2.706	3.841	6.635	7.879	10.828

A．	B．
C．	D．

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2022年河南省湘豫名校高考數(shù)學(xué)聯(lián)考試卷（文科）（3月份）

一、選擇題：本題共12小題，每小題5分，共60分，在每小題給出的四個選項中，只有一項符合題目要求．

1．命題“?x∈R，3x2+2x-5＜0”的否定是（ ）

2．平面直角坐標(biāo)系中，角α的終邊經(jīng)過點P（1，3），則sin（π2-α）=（ ）

3．已知等差數(shù)列{an}滿足a1=2，S5=S12，若am+a5=0，則m=（ ）

4．若實數(shù)x,y滿足約束條件2x-y≤0x-1≤0x+y-1≥0，則z=y-x的最小值是（ ）

5．若復(fù)數(shù)z滿足|z-1+i|=1，z在復(fù)平面內(nèi)對應(yīng)的點為（x,y），則（ ）

6．函數(shù)f（x）=2x2-1（x∈[2，6]）的最大值為（ ）

7．過點（0，3）且與曲線y=x3-2x+1相切的直線方程為（ ）

8．下列命題中，正確的是（ ）

9．已知直線l過定點（0，1），則“直線l與圓（x-2）2+y2=4相切”是“直線l的斜率為34”的（ ）

10．如圖陰影部分為已曲邊梯形，其曲線對應(yīng)函數(shù)為y=ex-1，在長方形內(nèi)隨機(jī)投擲一顆黃豆，則它落在陰影部分的概率是（ ）

11．已知集合A={x|x-1＞0}，B={x|x2-2x≤0}，則A∩B=（ ）

12．函數(shù)f（x）=xsin（π2+x）e|x|的圖象大致為（ ）

二、填空題：本題共4小題，每小題5分，共20分．

14．若將函數(shù)f（x）=sin（2x+φ）（0＜φ＜π）的圖象向右平移π3個單位長度后得到的圖象對應(yīng)函數(shù)為奇函數(shù)，則φ=．

16．已知點P為雙曲線x2a2-y2b2=1（a＞0，b＞0）右支上的一點，點F1，F(xiàn)2分別為雙曲線的左、右焦點，若M為△PF1F2的內(nèi)心，且S△PMF1=S△PMF2+12S△MF1F2，則雙曲線的離心率為 ．

三、解答題；共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟，第17～21題為必考題，每個試題考生都必須作答．第22、23題為選考題，考生根據(jù)要求作答．（一）必考題：共60分．

17．（1）已知a,b,c,d∈R求證：（a2+b2）（c2+d2）≥（ac+bd）2；（2）?a,b,c＞0，a+b+c=3，求證：a2+b2+c2≥3．

18．已知函數(shù)f（x）=ex-ln（x+m）．（1）當(dāng)m=12時，求曲線f（x）在點（0，f（0））處切線方程；（2）當(dāng)m≤2時，求證：f（x）＞0．

20．如圖，在三棱錐P-ABC中，高PC=4（PC⊥底面ABC），AB=BC=3，∠ABC=120°．（1）求三棱錐P-ABC的體積；（2）求三棱錐P-ABC外接球的表面積．

[選修4-4：坐標(biāo)系與參數(shù)方程]（共1小題，滿分10分）

[選修4-5：不等式選講]

1．命題“?x∈R，3x²+2x-5＜0”的否定是（　　）

2．平面直角坐標(biāo)系中，角α的終邊經(jīng)過點
P
（
1
，
3
）
，則
sin
（
π
2
-
α
）
=（　　）

3．已知等差數(shù)列{a_n}滿足a₁=2，S₅=S₁₂，若a_m+a₅=0，則m=（　　）

4．若實數(shù)x,y滿足約束條件
2
x
-
y
≤
0
x
-
1
≤
0
x
+
y
-
1
≥
0
，則z=y-x的最小值是（　　）

5．若復(fù)數(shù)z滿足|z-1+i|=1，z在復(fù)平面內(nèi)對應(yīng)的點為（x,y），則（　　）

6．函數(shù)
f
（
x
）
=
2
x
2
-
1
（x∈[2，6]）的最大值為（　　）

7．過點（0，3）且與曲線y=x³-2x+1相切的直線方程為（　　）

8．下列命題中，正確的是（　　）

9．已知直線l過定點（0，1），則“直線l與圓（x-2）²+y²=4相切”是“直線l的斜率為
3
4
”的（　　）

10．如圖陰影部分為已曲邊梯形，其曲線對應(yīng)函數(shù)為y=e^x-1，在長方形內(nèi)隨機(jī)投擲一顆黃豆，則它落在陰影部分的概率是（　　）

11．已知集合A={x|x-1＞0}，B={x|x²-2x≤0}，則A∩B=（　　）

12．函數(shù)f（x）=
xsin
（
π
2
+
x
）
e
|
x
|
的圖象大致為（　　）

14．若將函數(shù)f（x）=sin（2x+φ）（0＜φ＜π）的圖象向右平移
π
3
個單位長度后得到的圖象對應(yīng)函數(shù)為奇函數(shù)，則φ=
．

16．已知點P為雙曲線
x
2
a
2
-
y
2
b
2
=1（a＞0，b＞0）右支上的一點，點F₁，F(xiàn)₂分別為雙曲線的左、右焦點，若M為△PF₁F₂的內(nèi)心，且S_△PMF₁=S_△PMF₂+
1
2
S
△
M
F
1
F
2
，則雙曲線的離心率為
．

17．（1）已知a,b,c,d∈R求證：（a²+b²）（c²+d²）≥（ac+bd）²；
（2）?a,b,c＞0，a+b+c=3，求證：a²+b²+c²≥3．

18．已知函數(shù)f（x）=e^x-ln（x+m）．
（1）當(dāng)
m
=
1
2
時，求曲線f（x）在點（0，f（0））處切線方程；
（2）當(dāng)m≤2時，求證：f（x）＞0．

20．如圖，在三棱錐P-ABC中，高PC=4（PC⊥底面ABC），AB=BC=3，∠ABC=120°．
（1）求三棱錐P-ABC的體積；
（2）求三棱錐P-ABC外接球的表面積．