2020年吉林省延邊州高考數學模擬試卷(理科)(4月份)
發布:2025/11/12 21:0:28
一、選擇題:本題共12小題,每小題5分,共60分.在每小題給出的四個選項中,只有一項是符合題目要求的.
-
1.已知復數z滿足z(2+i7)=3+i,則復數z的虛部是( )
組卷:66引用:3難度:0.8解析 -
2.人們在進行工業設計時,巧妙地利用了圓錐曲線的光學性質.從雙曲線右焦點F2發出的光線通過雙曲線鏡面反射出發散光線,且反射光線的反向延長線經過左焦點F1.已知雙曲線的方程為x2-y2=1,則當入射光線F2P和反射光線PE互相垂直時(其中P為入射點),∠F1F2P的余弦值大小為( )
組卷:57引用:3難度:0.6解析 -
3.已知函數
,若關于x的方程f(x)=t有四個不同的實數解x1,x2,x3,x4,且x1<x2<x3<x4,則f(x)=x2+4x+2,x≤1,|log2(x-1)|,x>1,的最小值為( )(3+x1)(3-x2)+2x3+12x4組卷:270引用:4難度:0.5解析 -
4.已知空間中不過同一點的三條直線l,m,n,條件“l,m,n共面”成立的一個充分不必要條件是( )
組卷:94引用:2難度:0.7解析 -
5.將函數f(x)=2sin(ωx+
)(ω>0)的圖像向右平移π6個單位,得到函數y=g(x)的圖像,若y=g(x)在π6ω上為增函數,則ω的取值范圍是( )[0,π3]組卷:198引用:4難度:0.6解析 -
6.已知向量
,則實數k=( )a=(2,0),b=(1,3),(a+kb)⊥(ka-b)組卷:150引用:4難度:0.7解析 -
7.關于函數
,有下列命題:f(x)=lnx2+1|x|(x≠0,x∈R)
①函數y=f(x)的圖像關于y軸對稱;
②當-1<x<0或x>1時,f(x)為增函數;
③f(x)既有最大值,也有最小值;
其中命題正確的個數是( )組卷:3引用:1難度:0.7解析 -
8.圓x2+y2-4y=0關于直線y=2x+1對稱的圖形軌跡方程為( )
組卷:94引用:2難度:0.6解析 -
9.各項均為正數的等差數列{an}的前n項和是Sn,若
,則S17的值為( )a29-a7+12a5=0組卷:132引用:3難度:0.8解析 -
10.在如圖所示的韋恩圖中,A,B均是非空集合,則陰影部分表示的集合為( )
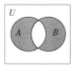 組卷:155引用:3難度:0.9
組卷:155引用:3難度:0.9解析 -
11.設20件產品中有5件不合格,從中任意取出2件,在所取得的產品中發現有一件不合格品,求另一件也是不合格品的概率為( )
組卷:10引用:1難度:0.7解析 -
12.系統找不到該試題
二、填空題:本題共4小題,每小題5分,共20分.
-
13.(x-3)(x-32)(x-33)(x-34)的展開式中x3的系數為 .(用數字作答)
組卷:897引用:2難度:0.6解析 -
14.下列說法:
①正切函數y=tanx在定義域內是增函數;
②函數是奇函數;f(x)=cos(23x+π2)
③是函數x=π8的一條對稱軸方程;f(x)=sin(2x+5π4)
④扇形的周長為8cm,面積為4cm2,則扇形的圓心角為2rad;
⑤若α是第三象限角,則取值的集合為{-2,0},|sinα2|sinα2+|cosα2|cosα2
其中正確的是.(寫出所有正確答案的序號)組卷:21引用:1難度:0.7解析 -
15.已知函數f(x)=excosx,則f(x)的導數f'(x)=.
組卷:405引用:3難度:0.8解析 -
16.已知正項數列{an}是公比為
的等比數列,數列{bn}的通項公式為12.若滿足an>bn的正整數n恰有3個,則a1的取值范圍為 .bn=n2組卷:22引用:2難度:0.7解析
三、解答題:共70分.解答應寫出文字說明,證明過程或演算步驟.第17~21題為必考題,每個試題考生都必須作答.第22、23題為選考題,考生根據要求作答.(一)必考題:60分.
-
 17.云浮市質監部門為迎接2015年春節到來,從市場中隨機抽取100個不同生產廠家的某種產品檢驗質量,按重量(單位;g)分組(重量大的質量高),得到的頻率分布表如圖所示:
17.云浮市質監部門為迎接2015年春節到來,從市場中隨機抽取100個不同生產廠家的某種產品檢驗質量,按重量(單位;g)分組(重量大的質量高),得到的頻率分布表如圖所示:
(1)請先求出頻率分布表中①、②位置相應數據,再完成下列頻率分布直方圖;組號 重量分組 頻數 頻率 第1組 [160,165) 5 0.050 第2組 [165,170) ① 0.350 第3組 [170,175) 30 ② 第4組 [175,180) 20 0.200 第5組 [180,185] 10 0.100 合計 100 1.00
(2)由于該產品要求質量高,決定在重量大的第3,4,5組中用分層抽樣抽取6個產品再次檢驗,求第3,4,5組每組各抽取多少產品進入第二次檢驗?組卷:16引用:3難度:0.5解析 -
18.在平面直角坐標系xOy中,以坐標原點為極點,x軸正半軸為極軸建立極坐標系,直線l的極坐標方程為ρcos(θ+
)=π4,曲線C的極坐標方程為ρ-6cosθ=0.22
(1)寫出直線l和曲線C的直角坐標方程;
(2)已知點A(1,0),若直線l與曲線C交于P,Q兩點,P,Q中點為M,求的值.|AP||AQ||AM|組卷:150引用:6難度:0.7解析 -
19.已知函數f(x)=xlnx+ax2-1,且f′(1)=-1.
(Ⅰ)求f(x)的解析式;
(Ⅱ)若對于任意x∈(0,+∞),都有f(x)-mx≤-1,求m的最小值;
(Ⅲ)證明:函數y=f(x)-xex+x2的圖象在直線y=-2x-1的下方.組卷:226引用:8難度:0.1解析 -
20.在△ABC中,a=3,
,c=2,求∠B,S△ABC.b=7組卷:4引用:1難度:0.7解析 -
21.已知a、b均為正數,設f(x)=6-|x+a|-|x-b|;
(1)當a=1,b=2時,求不等式f(x)>0的解集;
(2)若f(x)的最大值為3,求的最小值.1a+1b組卷:13引用:2難度:0.6解析
(二)選考題:共10分.請考生在第22、23題中任選一題作答,如果多做,則按所做的第一題計分.
-
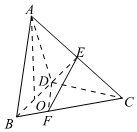 22.在三棱錐A-BCD中,已知CB=CD=,BD=2,O為BD的中點,AO⊥平面BCD,5
22.在三棱錐A-BCD中,已知CB=CD=,BD=2,O為BD的中點,AO⊥平面BCD,5
AO=2,E為AC的中點.點F在BC上,滿足BF=BC.14
(1)求點A到平面DEF的距離;
(2)求直線BD與平面DEC所成角的余弦值.組卷:273引用:6難度:0.6解析 -
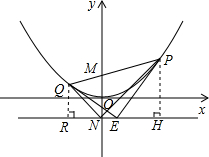 23.已知點M,N的坐標分別是(0,2)和(0,-2),點P是二次函數的圖象上的一個動點.y=18x2
23.已知點M,N的坐標分別是(0,2)和(0,-2),點P是二次函數的圖象上的一個動點.y=18x2
(1)判斷以點P為圓心,PM為半徑的圓與直線y=-2的位置關系,并說明理由;
(2)設直線PM與二次函數的圖象的另一個交點為Q,連接NP,NQ,求證:∠PNM=∠QNM;y=18x2
(3)過點P,Q分別作直線y=-2的垂線,垂足分別為H,R,取RH中點為E,求證:QE⊥PE.組卷:12引用:1難度:0.1解析


