2020年天津市河西區高考數學二模試卷

一、選擇題：在每小題給出的四個選項中，只有一項是符合題目要求的．

• 1．已知a,b,c∈R，在下列條件中，使得a＜b成立的一個充分而不必要條件是（　　）

  A．（a-b）c2＜0

  B．a3＜b3

  C． 1 a ＜ 1 b

  D．a2＜b2
  組卷：195引用：4難度：0.8

  解析

• 2．函數y=sinx-xcosx的部分圖象是（　　）

  A．

  B．

  C．

  D．
  組卷：120引用：8難度：0.8

  解析

• 3．已知集合

  U

  =

  {

  0

  ，

  1

  ，

  2

  ，

  3

  ，

  4

  }

  ，

  A

  =

  {

  x

  ∈

  N

  |

  3

  x

  ∈

  N

  }

  ，則?_UA=（　　）

  A．{0，1，3}

  B．{1，3}

  C．{0，2，4}

  D．{2，4}
  組卷：174引用：4難度：0.8

  解析

• 4．經濟學專業的學生們為研究流通費率y和銷售額x（單位：千萬元）的關系，對同類型10家企業的相關數據（x_i，y_i）（i=1，2，?，10）進行整理，并得到如圖散點圖：
  
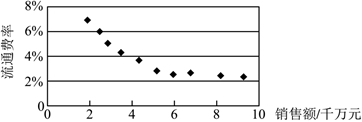
  由此散點圖，在2千萬元至1億元之間，下面四個回歸方程類型中最適宜作為流通費率y和銷售額x的回歸方程類型的是（　　）

  A．y=ax+b

  B．y=ax2+b

  C．y=aex+b

  D．y=alnx+b
  組卷：144引用：3難度：0.7

  解析

• 5．已知△ABC中，角A，B，C的對邊分別為a,b,c,且

  a

  =

  2

  ，

  b

  =

  6

  ，

  A

  =

  30

  °

  ，則c=（　　）

  A． 2

  B． 2 2

  C． 2 或 2 2

  D．2或 3
  組卷：288引用：8難度：0.7

  解析

• 6．由1，2，3，4，5五個數字可以組成多少個無重復數字且1和2相鄰的五位數（　　）

  A．24

  B．48

  C．12

  D．120
  組卷：177引用：2難度：0.8

  解析

• 7．過圓柱的上，下底面圓圓心的平面截圓柱所得的截面是面積為16的正方形，則圓柱的側面積是（　　）

  A． 12 2 π

  B．16π

  C．8π

  D．10π
  組卷：100引用：2難度：0.8

  解析
• 8．系統找不到該試題
• 9．系統找不到該試題

二、填空題：本大題共6小題，每小題5分，共30分．

• 10．（x-1）（x-

  2

  x

  ）⁶展開式中的常數項為

  （用數字作答）．
  組卷：78引用：4難度：0.7

  解析

• 11．離散型隨機變量ξ的分布列如下表所示，p=

  ，D（ξ）=

  ．
  

  ξ	0	1
  P	1 3	p
  組卷：36引用：1難度：0.7

  解析

• 12．已知i為虛數單位，則

  2

  -

  i

  1

  +

  i

  =

   

  ．
  組卷：282引用：6難度：0.7

  解析

• 13．在△ABC中，有

  AB

  ?（

  AC

  -

  CB

  ）=3

  BC

  ?（

  BA

  -

  AC

  ），則tanB的最大值是

  ．
  組卷：48引用：2難度：0.5

  解析

• 14．過圓x²+y²=5上一點M（1，2）的圓的切線方程為

   

  ．
  組卷：40引用：6難度：0.5

  解析

• 15．若x＞1，則x+

  1

  x

  -

  1

  的最小值是

  ．
  組卷：1932引用：41難度：0.7

  解析

三、解答題：本大題共5小題，共75分，解答應寫出文字說明，證明過程或演算步驟．

• 16．判斷下列說法是否正確，正確的在橫線上打“√”，錯誤的打“×”．
  （1）平面內到兩定點的距離的差等于常數（小于兩定點間的距離）的點的軌跡是雙曲線．

  
  （2）在雙曲線的標準方程

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1中，a＞0，b＞0，且a≠b.

  
  （3）在雙曲線的標準方程中，a,b的大小關系是a＞b.
  組卷：5引用：0難度：0.7

  解析

• 17．已知函數f（x）=x³-x,g（x）=2x-3．
  （Ⅰ）求曲線y=f（x）在點（1，f（1））處的切線方程；
  （Ⅱ）求函數f（x）在[0，2]上的最大值；
  （Ⅲ）求證：存在唯一的x₀，使得f（x₀）=g（x₀）．
  組卷：126引用：9難度：0.3

  解析

• 18．已知橢圓的焦點坐標為F₁（-1，0），F₂（1，0），過F₂作垂直于長軸的直線交橢圓于A、B兩點，且|AB|=3．
  （1）求橢圓的方程；
  （2）過F₁點作相互垂直的直線l₁，l₂，其中l₁交橢圓于P₁，P₂，l₂交橢圓于P₃，P₄，求證

  1

  |

  P

  1

  P

  2

  |

  +

  1

  |

  P

  3

  P

  4

  |

  是否為定值？并求當四邊形P₁P₂P₃P₄面積的最小值．
  組卷：60引用：1難度：0.3

  解析

• 19．已知f（x）是定義在R上的偶函數，且x≤0時，f（x）=x²+2x.
  （1）求f（x）的解析式；
  （2）畫出f（x）的圖象，若f（x）的圖象與函數g（x）=m的圖象有四個不同的交點，求m的取值范圍．
  組卷：4引用：2難度：0.5

  解析

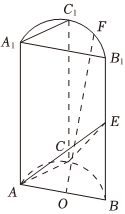• 20．如圖，A，B，C為圓柱底面圓周上三個不同的點，AA₁，BB₁，CC₁分別為半圓柱的三條母線，且C是

  ?

  AB

  的中點，O，E分別為AB，BB₁的中點．
  （1）證明：A₁C₁∥平面ACE．
  （2）若AA₁=4AB=8，F是

  ?

  A

  1

  B

  1

  上的動點（含弧的端點），求OF與平面ACE所成角的正弦值的最大值．
  組卷：84引用：5難度：0.4

  解析