2020年陜西省西安市高新一中高考數學模擬試卷(文科)(3月份)
發布:2025/11/13 2:0:24
一、選擇題(本大題共12小題,每小題5分,共60分,在每小題給出的四個選項中,只有一個選項是符合題目要求的)
-
1.在△ABC中,sin2A≤sin2B+sin2C-sinBsinC,則A的取值范圍是( )
組卷:6180引用:134難度:0.9解析 -
2.已知復數z=
(i為虛數單位),則z的共軛復數對應的點位于復平面的( )5i1-2i組卷:135引用:10難度:0.8解析 -
 3.如圖,在正方體ABCD-A1B1C1D1中,點E,F分別是棱B1B,B1C1的中點,點G是棱C1C的中點,則過線段AG且平行于平面A1EF的截面圖形為( )組卷:393引用:5難度:0.5
3.如圖,在正方體ABCD-A1B1C1D1中,點E,F分別是棱B1B,B1C1的中點,點G是棱C1C的中點,則過線段AG且平行于平面A1EF的截面圖形為( )組卷:393引用:5難度:0.5解析 -
4.已知
,a=(22)12,c=ln3,則( )b=(45)13組卷:59引用:1難度:0.7解析 -
5.將函數y=sin(2x+φ)(
)的圖象向右平移|φ|<π2個單位長度,得到函數圖象關于y軸對稱,則φ的值為( )π6組卷:153引用:4難度:0.7解析 -
6.甲、乙兩位同學從5本不同的課外讀物中各自選讀1本,則這兩人選讀的讀物不同的選法有( )
組卷:32引用:3難度:0.9解析 -
7.若集合A={x|-3<x<3},B={y|y=x2-2,x∈R},則A∩B=( )
組卷:18引用:1難度:0.8解析 -
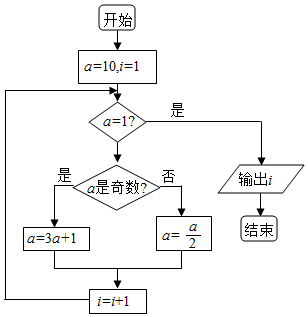 8.“考拉茲猜想”又名“3n+1猜想”或“奇偶歸一猜想”,是指對于每一個正整數,如果它是奇數,則對它乘3再加1;如果它是偶數,則對它除以2.如此循環,最終都能得到1.閱讀如圖所示的程序框圖,運行相應程序,輸出的結果i=( )組卷:427引用:8難度:0.7
8.“考拉茲猜想”又名“3n+1猜想”或“奇偶歸一猜想”,是指對于每一個正整數,如果它是奇數,則對它乘3再加1;如果它是偶數,則對它除以2.如此循環,最終都能得到1.閱讀如圖所示的程序框圖,運行相應程序,輸出的結果i=( )組卷:427引用:8難度:0.7解析 -
9.下列命題正確的是( )
組卷:42引用:10難度:0.9解析 -
10.“
”是“a2=b2”的( )(a)2=(b)2組卷:54引用:3難度:0.9解析 -
11.已知函數f(x)=
,則函數f(x)=( )2x-1,x∈[-2,1)∪(1,6]組卷:59引用:1難度:0.6解析 -
 12.一水池有2個進水口,1個出水口,進出水速度如圖甲、乙所示.某天0點到6點,該水池的蓄水量如圖丙所示.(至少打開一個水口)給出以下3個論斷:
12.一水池有2個進水口,1個出水口,進出水速度如圖甲、乙所示.某天0點到6點,該水池的蓄水量如圖丙所示.(至少打開一個水口)給出以下3個論斷:
①0點到3點只進水不出水;
②3點到4點不進水只出水;
③4點到6點不進水不出水.
則正確論斷的個數是( )組卷:46引用:8難度:0.9解析
二、填空題(本大題共4小題,每小題5分,共20分)
-
13.已知雙曲線E:x2-
=1的左、右焦點分別為F1,F2,A(2,3)是E上一點,直線AF1與E的另一個交點為B,則△ABF2的周長為 .y23組卷:38引用:2難度:0.7解析 -
14.橢圓
的左焦點為F,直線x=m與橢圓相交于A,B兩點,當△FAB的周長最大時,△FAB的面積為ab.若b=1,則橢圓的準線方程是.x2a2+y2b2=1(a>b>0)組卷:52引用:1難度:0.7解析 -
15.若等差數列的前6項和為23,前9項和為57,則數列的前n項和Sn=.
組卷:1536引用:17難度:0.7解析 -
16.已知圓x2+y2-4x-6y=0,則過點M(1,1)的最短弦所在的直線方程是.
組卷:662引用:4難度:0.7解析
三、解答題(本大題共5小題,共70分.解答應寫出文字說明、證明過程或演算步驟)
-
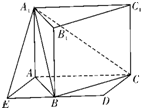 17.如圖,側棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四邊形ACDE中,AE=2,AC=4,∠AEB=60°,點B為DE中點,連接A1E.
17.如圖,側棱垂直底面的三棱柱ABC-A1B1C1的底面ABC位于平行四邊形ACDE中,AE=2,AC=4,∠AEB=60°,點B為DE中點,連接A1E.
(1)求證:平面A1BC⊥平面A1ABB1;
(2)設四棱錐A1-AEBC與四棱錐A1-B1BCC1的體積分別為V1,V2,求V1:V2的值.組卷:32引用:1難度:0.5解析 -
18.已知拋物線C:y2=2px(p>0)的焦點為F(1,0),點M在直線x=-2上運動,直線l1,l2經過點M,且與C分別相切于A,B兩點.
(1)求C的方程;
(2)試問直線AB是否過定點?若是,求出該定點坐標;若不是,請說明理由.組卷:70引用:4難度:0.5解析 -
19.已知數列{an}是公差為2的等差數列,其前8項的和為64.數列{bn}是公比大于0的等比數列,b1=4,b3-b2=48.
(1)求數列{an}和{bn}的通項公式;
(2)記cn=b2n+,n∈N*.1bn
(i)證明:{-c2n}是等比數列;c2n
(ii)證明:<2n∑k=1akak+1c2k-c2k(n∈N*).2組卷:4836引用:6難度:0.5解析 -
20.某單位10000人,想通過驗血的方式篩查出某種病毒的攜帶者,如果對每個人的血樣逐一化驗,需要化驗10000次,統計專家提出了一種方法:隨機地按10人一組分組,然后將各組10個人的血樣混合再化驗,如果混合血樣呈陰性,說明這10個人全部陰性;如果混合血樣呈陽性,說明其中至少有一個人呈陽性,就需要對這組的每個人再分別化驗一次.假設該單位攜帶病毒的人數有200人.(0.985≈0.90)
(1)用樣本的頻率估計概率,若5個人一組,求一組混合血樣呈陽性的概率;
(2)用統計專家這種方法按照5個人一組或10個人一組,問哪種分組方式篩查出這10000人中該病毒攜帶者需要化驗次數較少?為什么?組卷:29引用:1難度:0.7解析 -
21.已知函數f(x)=|x-m|-|x-3m-1|.
(1)若m=1,求不等式f(x)<1的解集.
(2)對任意的x∈R,有f(x)≤f(2),求實數m的取值范圍.組卷:71引用:8難度:0.6解析
請考生在第22、23兩題中任選-一題作答.女做,則按所做的第一個題目計分.[選修44:坐標系與參數方程]
-
22.已知函數
.f(x)=x3+32x2-4ax+2
(1)若函數g(x)=6lnx-x3+(4a-9)x+f(x),求g(x)的單調區間;
(2)若f(x)有兩個都小于0的極值點,求實數a的取值范圍.組卷:205引用:8難度:0.6解析
[選修4-5:不等式選講]
-
23.在平面直角坐標系中,已知直線l的參數方程為
,(t為參數),曲線C的方程為x2+y2+8y+7=0.以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系.x=tcosαy=tsinα
(1)求直線l及曲線C的極坐標方程;
(2)設直線l與曲線C相交于M,N兩點,滿足||OM|-|ON||=2,求直線l的斜率.5組卷:170引用:4難度:0.7解析


