精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

當前位置：試卷中心 > 試卷詳情

2023-2024學年福建省莆田二十五中高三（上）返校數學試卷

發布：2025/11/13 6:0:28

一、單項選擇題（本大題共8小題，每小題5分，共40分）

1．若雙曲線
y
2
2
-
x
2
m
=
1
的焦點與橢圓
x
2
3
+
y
2
4
=
1
的長軸端點重合，則m的值為（　　）
A．2 B．4 C．-2 D．-4
組卷：162引用：5難度：0.8
2．已知矩形ABCD中，AB=3，BC=2，將△CBD沿BD折起至△C'BD．當直線C'B與AD所成的角最大時，三棱錐C'-ABD的體積為（　　）
A．
5
3
B．
5
13
13
C．
2
5
3
D．
6
13
13
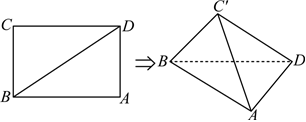組卷：112引用：3難度：0.5
3．
（
3
x
+
1
）
（
1
x
-
1
）
5
的展開式中的常數項為（　　）
A．14 B．-14 C．16 D．-16
組卷：455引用：4難度：0.7
4．cos20°cos25°-cos70°sin25°=（　　）
A．
1
2
B．
2
2
C．
3
2
D．1
組卷：605引用：2難度：0.9
5．把某種物體放在空氣中冷卻，若該物體原來的溫度是θ₁℃，空氣的溫度是θ₀℃，則tmin后該物體的溫度θ℃可由公式
θ
=
θ
0
+
（
θ
1
-
θ
0
）
e
-
t
4
求得．若將溫度分別為100℃和60℃的兩塊物體放入溫度是20℃的空氣中冷卻，要使得這兩塊物體的溫度之差不超過10℃，至少要經過（　　）（取：ln2=0.69）
A．2.76min B．4.14min C．5.52min D．6.9min
組卷：85引用：11難度：0.8
6．已知復數z=
5
2
+
i
，則其共軛復數
z
=（　　）
A．2+i B．2-i C．10+5i D．10-5i
組卷：107引用：2難度：0.8
7．已知集合A={x|x²-3x+2=0}，B={x|0≤x≤5，x∈N}，則滿足條件A?C?B的集合C的個數為（　　）
A．15 B．16 C．7 D．8
組卷：124引用：3難度：0.7
8．已知A（1，1，0），B（0，3，0），C（2，2，3），則向量
AC
在
AB
上的投影向量的坐標是（　　）
A．
（
-
1
5
，
2
5
，
0
）
B．
（
-
1
5
，
2
5
，
1
）
C．
（
-
1
5
，-
2
5
，
0
）
D．
（
1
5
，
2
5
，
0
）
組卷：40引用：2難度：0.8

二、多項選擇題（本大題共4小題，每小題5分，共20分）

9．已知函數f（x）=e^x-e^-x-cos2x,若f（x₁）＞f（x₂），則（　　）
A．
e
x
1
-
x
2
＞
1
B．
x
3
1
＞
x
3
2
C．ln|x₁|＞ln|x₂| D．x₁|x₁|＞x₂|x₂|
組卷：49引用：5難度：0.6
10．數學上有很多著名的猜想，“角谷猜想”（又稱“冰雹猜想”）就是其中之一，它是指任取一個正整數，若是奇數，就將該數乘3再加上1；若是偶數，就將該數除以2．反復進行上述兩種運算，經過有限次步驟后，必進入循環圈1→4→2→1．記正整數a₀按照上述規則實施第n（n∈N）次運算的結果為a_n，若a₅=1，則a₀可能為（　　）
A．32 B．16 C．5 D．4
組卷：19引用：2難度：0.6
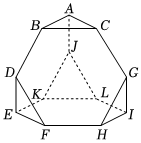11．截角四面體是一種半正八面體，可由四面體經過適當的截角，即截去四面體的四個頂點所產生的多面體．如圖所示，將棱長為3a的正四面體沿棱的三等分點作平行于底面的截面，得到所有棱長均為a的截角四面體，則下列說法正確的是（　　）
A．AB⊥CG
B．二面角B-FH-K的平面角余弦值為
1
3
C．該截角四面體的外接球表面積為
11
2
π
a
2
D．該截角四面體的表面積為
6
3
a
2
組卷：70引用：4難度：0.5
12．已知正數x,y滿足x²=y³＜1，則下列結論正確的是（　　）
A．0＜x＜y＜1 B．0＜y＜x＜1 C．
|
y
-
x
|
≤
4
27
D．
|
y
2
-
x
2
|
≤
4
27
組卷：74引用：6難度：0.6

三、填空題（本大題共4小題，每小題5分，共20分）

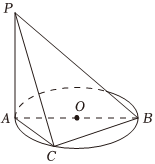13．如圖所示，直線PA垂直于圓O所在的平面，△ABC內接于圓O，且AB為圓O的直徑，PA=AB=2．現有以下命題：
①BC⊥PC；
②當點C在圓周上由B點逐步向A點移動過程中，二面角B-PC-A會逐步增大；
③當點C在圓周上由B點逐步向A點移動過程中，三棱錐B-PAC的體積的最大值為
2
3
．
其中正確的命題序號為
．
組卷：75引用：2難度：0.5
14．函數f（x）=xe^x-lnx-1，若不等式f（x）≥2ax恒成立，則實數a的取值范圍為
．
組卷：90引用：2難度：0.5
15．若直線y=kx+b是曲線y=lnx的切線，也是曲線y=e^x-2的切線，則k=
．
組卷：302引用：6難度：0.6
16．隨機變量X服從正態分布N（2，σ²），若P（X＜3）=P（a＜X≤2）+
1
2
，則實數a=
．
組卷：93引用：1難度：0.7

四、解答題（本大題共6小題，共70分）

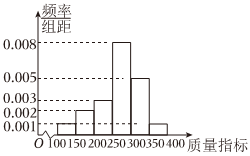17．某企業從生產的一批零件中抽取100件產品作為樣本，檢測其質量指標值m（其中：100≤m≤400），得到頻率分布直方圖，并依據質量指標值劃分等級如表所示：

質量指標值m 150≤m＜350 100≤m＜150或350≤m≤400

等級 A級 B級

（1）從樣本的B級零件中隨機抽3件，記其中質量指標值在[350，400]的零件的件數為ξ，求ξ的分布列和數學期望；
（2）該企業為節省檢測成本，采用混裝的方式將所有的零件按500件一箱包裝，已知一個A級零件的利潤是10元，一個B級零件的利潤是5元，以樣本分布的頻率作為總體分布的概率，試估計每箱零件的利潤．
組卷：11引用：1難度：0.5
18．已知函數f（x）=e^x（ax²-x-1）．
（1）求曲線y=f（x）在點（0，-1）處的切線方程；
（2）若f（x）在x=-2處取得極大值，求a的取值范圍；
（3）求證：當a≥1時，f（x）≥-e.
組卷：148引用：3難度：0.5
19．已知等差數列{a_n}的公差d不為0，a₄=7，且a₁，a₃，a₁₃成等比數列．
（1）求數列{a_n}的前n項和S_n；
（2）記
b
n
=
1
a
n
a
n
+
1
，
n
∈
N
*
，證明：
b
1
+
b
2
+
b
3
+
?
+
b
n
＜
1
2
．
組卷：68引用：3難度：0.5
20．已知橢圓
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的焦距為4，設右焦點為F₁，離心率為e.
（1）若
e
=
2
2
，求橢圓的方程；
（2）設A、B為橢圓上關于原點對稱的兩點，AF₁的中點為M，BF₁的中點為N，若原點O在以線段MN為直徑的圓上．
①證明點A在定圓上；
②設直線AB的斜率為k,若
k
≥
3
，求e的取值范圍．
組卷：832引用：4難度：0.3
21．
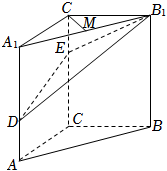
如圖，在三棱柱ABC-A₁B₁C₁中，CC₁⊥平面ABC，AC⊥BC，AC=BC=2，CC₁=3，點D，E分別在棱AA₁和棱CC₁上，且AD=1CE=2，M為棱A₁B₁的中點．
（Ⅰ）求證：C₁M⊥B₁D；
（Ⅱ）求二面角B-B₁E-D的正弦值；
（Ⅲ）求直線AB與平面DB₁E所成角的正弦值．
組卷：154引用：3難度：0.5
22．在△ABC中，A，B，C的對邊分別為a,b,c,acosB-2acosC=（2c-b）cosA．
（1）若c=
3
a,求cosB的值；
（2）若b=1，∠BAC的平分線AD交BC于點D，求AD長度的取值范圍．
組卷：1786引用：14難度：0.6

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ - 1 5 ， 2 5 ， 0 ）	B．（ - 1 5 ， 2 5 ， 1 ）
C．（ - 1 5 ，- 2 5 ， 0 ）	D．（ 1 5 ， 2 5 ， 0 ）

質量指標值m	150≤m＜350	100≤m＜150或350≤m≤400
等級	A級	B級

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2023-2024學年福建省莆田二十五中高三（上）返校數學試卷

一、單項選擇題（本大題共8小題，每小題5分，共40分）

1．若雙曲線y22-x2m=1的焦點與橢圓x23+y24=1的長軸端點重合，則m的值為（ ）

2．已知矩形ABCD中，AB=3，BC=2，將△CBD沿BD折起至△C'BD．當直線C'B與AD所成的角最大時，三棱錐C'-ABD的體積為（ ）

3．（3x+1）（1x-1）5的展開式中的常數項為（ ）

4．cos20°cos25°-cos70°sin25°=（ ）

6．已知復數z=52+i，則其共軛復數z=（ ）

7．已知集合A={x|x2-3x+2=0}，B={x|0≤x≤5，x∈N}，則滿足條件A?C?B的集合C的個數為（ ）

8．已知A（1，1，0），B（0，3，0），C（2，2，3），則向量AC在AB上的投影向量的坐標是（ ）

二、多項選擇題（本大題共4小題，每小題5分，共20分）

9．已知函數f（x）=ex-e-x-cos2x,若f（x1）＞f（x2），則（ ）

12．已知正數x,y滿足x2=y3＜1，則下列結論正確的是（ ）

三、填空題（本大題共4小題，每小題5分，共20分）

14．函數f（x）=xex-lnx-1，若不等式f（x）≥2ax恒成立，則實數a的取值范圍為 ．

15．若直線y=kx+b是曲線y=lnx的切線，也是曲線y=ex-2的切線，則k=．

16．隨機變量X服從正態分布N（2，σ2），若P（X＜3）=P（a＜X≤2）+12，則實數a=．

四、解答題（本大題共6小題，共70分）

18．已知函數f（x）=ex（ax2-x-1）．（1）求曲線y=f（x）在點（0，-1）處的切線方程；（2）若f（x）在x=-2處取得極大值，求a的取值范圍；（3）求證：當a≥1時，f（x）≥-e.

19．已知等差數列{an}的公差d不為0，a4=7，且a1，a3，a13成等比數列．（1）求數列{an}的前n項和Sn；（2）記bn=1anan+1，n∈N*，證明：b1+b2+b3+?+bn＜12．

21．如圖，在三棱柱ABC-A1B1C1中，CC1⊥平面ABC，AC⊥BC，AC=BC=2，CC1=3，點D，E分別在棱AA1和棱CC1上，且AD=1CE=2，M為棱A1B1的中點．（Ⅰ）求證：C1M⊥B1D；（Ⅱ）求二面角B-B1E-D的正弦值；（Ⅲ）求直線AB與平面DB1E所成角的正弦值．

22．在△ABC中，A，B，C的對邊分別為a,b,c,acosB-2acosC=（2c-b）cosA．（1）若c=3a,求cosB的值；（2）若b=1，∠BAC的平分線AD交BC于點D，求AD長度的取值范圍．

1．若雙曲線
y
2
2
-
x
2
m
=
1
的焦點與橢圓
x
2
3
+
y
2
4
=
1
的長軸端點重合，則m的值為（　　）

2．已知矩形ABCD中，AB=3，BC=2，將△CBD沿BD折起至△C'BD．當直線C'B與AD所成的角最大時，三棱錐C'-ABD的體積為（　　）

3．
（
3
x
+
1
）
（
1
x
-
1
）
5
的展開式中的常數項為（　　）

4．cos20°cos25°-cos70°sin25°=（　　）

6．已知復數z=
5
2
+
i
，則其共軛復數
z
=（　　）

7．已知集合A={x|x²-3x+2=0}，B={x|0≤x≤5，x∈N}，則滿足條件A?C?B的集合C的個數為（　　）

8．已知A（1，1，0），B（0，3，0），C（2，2，3），則向量
AC
在
AB
上的投影向量的坐標是（　　）

9．已知函數f（x）=e^x-e^-x-cos2x,若f（x₁）＞f（x₂），則（　　）

12．已知正數x,y滿足x²=y³＜1，則下列結論正確的是（　　）

14．函數f（x）=xe^x-lnx-1，若不等式f（x）≥2ax恒成立，則實數a的取值范圍為
．

15．若直線y=kx+b是曲線y=lnx的切線，也是曲線y=e^x-2的切線，則k=
．

16．隨機變量X服從正態分布N（2，σ²），若P（X＜3）=P（a＜X≤2）+
1
2
，則實數a=
．

18．已知函數f（x）=e^x（ax²-x-1）．
（1）求曲線y=f（x）在點（0，-1）處的切線方程；
（2）若f（x）在x=-2處取得極大值，求a的取值范圍；
（3）求證：當a≥1時，f（x）≥-e.

19．已知等差數列{a_n}的公差d不為0，a₄=7，且a₁，a₃，a₁₃成等比數列．
（1）求數列{a_n}的前n項和S_n；
（2）記
b
n
=
1
a
n
a
n
+
1
，
n
∈
N
*
，證明：
b
1
+
b
2
+
b
3
+
?
+
b
n
＜
1
2
．

22．在△ABC中，A，B，C的對邊分別為a,b,c,acosB-2acosC=（2c-b）cosA．
（1）若c=
3
a,求cosB的值；
（2）若b=1，∠BAC的平分線AD交BC于點D，求AD長度的取值范圍．