2021-2022學年四川省瀘州市高一（上）期末數學試卷

一、選擇題：本大題共有12個小題，每小題5分，共60分．每小題給出的四個選項中，只有一項是符合要求的．

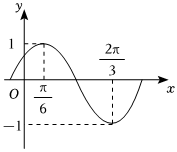• 1．已知函數f（x）=sin（ωx+φ）

  （

  ω

  ＞

  0

  ，

  |

  φ

  |

  ＜

  π

  2

  ）

  的部分圖象如圖所示，則（　　）

  A．ω=2，φ= π 6

  B． ω = 2 ， φ = - π 6

  C． ω = 1 ， φ = π 6

  D． ω = 1 ， φ = π 3
  組卷：416引用：5難度：0.5

  解析

• 2．若角α始邊為x軸非負半軸，終邊上一點A（1，-

  3

  ），則sinα等于（　　）

  A． 1 2

  B．- 1 2

  C． 3 2

  D．- 3 2
  組卷：75引用：2難度：0.9

  解析

• 3．如圖是杭州2022年第19屆亞運會會徽，名為“潮涌”，象征著新時代中國特色社會主義大潮的涌動和發展．如圖是會徽的幾何圖形．設弧AD的長度是l₁，弧BC的長度是l₂，幾何圖形ABCD面積為S₁，扇形BOC面積為S₂，若

  l

  1

  l

  2

  =3，則

  S

  1

  S

  2

  =（　　）
  

  A．3

  B．4

  C．6

  D．8
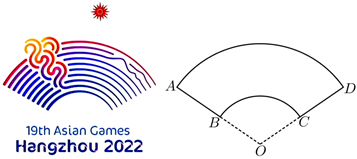  組卷：233引用：6難度：0.7

  解析

• 4．設a=3^0.3，b=0.3³，c=log₃0.3，則a,b,c的大小是（　　）

  A．a＜b＜c

  B．b＜c＜a

  C．b＞a＞c

  D．a＞b＞c
  組卷：149引用：3難度：0.8

  解析

• 5．設函數y=sinx的定義域為[a,b]，值域為[-

  1

  2

  ，1]，給出以下四個結論：
  ①b-a的最小值為

  2

  π

  3

  
  ②b-a的最大值為

  4

  π

  3

  
  ③a可能等于2kπ-

  π

  6

  （k∈z）     
  ④b可能等于2kπ-

  π

  6

  （k∈z）
  其中正確的有（　　）

  A．4個

  B．3個

  C．2個

  D．1個
  組卷：68引用：2難度：0.9

  解析

• 6．sin

  17

  π

  6

  等于（　　）

  A． 1 2

  B．- 1 2

  C． 3 2

  D．- 3 2
  組卷：287引用：7難度：0.9

  解析

• 7．如圖，射線l和圓C，當l從l₀開始在平面上繞端點O按逆時針方向勻速轉動（轉動角度不超過180°）時，它掃過的圓內陰影部分的面積S是時間t的函數，這個函數的圖象大致是（　　）

  A．

  B．

  C．

  D．
  組卷：40引用：2難度：0.7

  解析

• 8．設a=0.8^0.8，b=0.8^0.9，c=0.9^0.8，則a,b,c的大小關系是（　　）

  A．c＞b＞a

  B．a＞b＞c

  C．a＞c＞b

  D．c＞a＞b
  組卷：371引用：1難度：0.7

  解析

• 9．下列關于零向量的說法正確的是（　　）

  A．零向量沒有大小

  B．零向量沒有方向

  C．兩個反方向向量之和為零向量

  D．零向量與任何向量都共線
  組卷：269引用：1難度：0.8

  解析

• 10．已知冪函數

  f

  （

  x

  ）

  =

  （

  m

  2

  -

  m

  -

  1

  ）

  x

  m

  2

  -

  2

  m

  -

  2

  在（0，+∞）上遞增，則m=（　　）

  A．2

  B．4

  C．-1

  D．2或-1
  組卷：663引用：12難度：0.7

  解析

• 11．設集合U=R，集合M={x|x＜1}，N={x|-1＜x＜2}，則?_U（M∪N）=（　　）

  A．{x|x≥2}

  B．{x|x＞1}

  C．{x|x≥-1}

  D．{x|x＜2}
  組卷：92引用：2難度：0.8

  解析
• 12．系統找不到該試題

二、填空題：本大題共4個小題，每小題5分，共20分．

• 13．函數

  y

  =

  sin

  πx

  2

  的最小正周期是

  ．
  組卷：20引用：2難度：0.9

  解析

• 14．函數

  y

  =

  sin

  （

  π

  6

  -

  x

  ）

  ，

  x

  ∈

  [

  0

  ，

  3

  π

  2

  ]

  的單調遞減區間是

   

  ．
  組卷：427引用：2難度：0.7

  解析

• 15．向量

  a

  =（2k+3，3k+2）與

  b

  =（3，k）共線，則k=

  ．
  組卷：67引用：4難度：0.7

  解析

• 16．函數f（x）是[b-1，2]上的奇函數，則b=

  ．
  組卷：65引用：1難度：0.9

  解析

三、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．

• 17．如圖，在△ABC中

  AM

  =

  1

  3

  AB

  ，

  BN

  =

  1

  2

  BC

  ．設

  AB

  =

  a

  ，

  AC

  =

  b

  ．
  （1）用

  a

  ，

  b

  表示

  BC

  ，

  MN

  ；
  （2）若P為△ABC內部一點，且

  AP

  =

  5

  12

  a

  +

  1

  4

  b

  ，求證：M，P，N三點共線，并指明點P的具體位置．
  組卷：136引用：4難度：0.6

  解析

• 18．已知函數

  f

  （

  x

  ）

  =

  2

  x

  -

  1

  2

  x

  +

  1

  +

  2

  ．
  （1）判斷函數f（x）的單調性，并用定義法證明；
  （2）若不等式f（k?3^x）+f（3^x-9^x-4）＜0對任意x∈R恒成立，求實數k的取值范圍．
  組卷：58引用：2難度：0.5

  解析

• 19．設集合A={x|x²-8x+15=0}，B={x|ax-1=0}．
  （1）若a=

  1

  5

  ，判斷集合A與B的關系；
  （2）若A∩B=B，求實數a組成的集合C．
  組卷：663引用：11難度：0.7

  解析

• 20．對于函數f₁（x），f₂（x），如果存在實數a,b,使得f（x）=af₁（x）-bf₂（x），那么稱f（x）為f₁（x），f₂（x）的親子函數．
  （1）已知f₁（x）=2x-3，f₂（x）=x+1，試判斷f（x）=4x-11是否為f₁（x），f₂（x）的親子函數，若是，求出a,b；若不是，說明理由；
  （2）已知f₁（x）=3^x，f₂（x）=9^x，f（x）為f₁（x），f₂（x）的親子函數，且a=4，b=1．
  （i）若g（x）=（m+1）f₂（x）-f（x）+1，當-1≤x≤0時，g（x）≤0恒成立，求正數m的取值范圍；
  （ⅱ）若關于x的方程f（x）=nf₂（x）+1有實數解，求實數n的取值范圍．
  組卷：5引用：1難度：0.5

  解析

• 21．新冠肺炎疫情造成醫用防護服短缺，某地政府決定為防護服生產企業A公司擴大生產提供x（x∈[0，10]）（萬元）的專項補貼，并以每套80元的價格收購其生產的全部防護服，A公司在收到政府x（萬元）補貼后，防護服產量將增加到

  t

  =

  k

  ?

  （

  6

  -

  12

  x

  +

  4

  ）

  （萬件），其中k為工廠工人的復工率（k∈[0.5，1]），A公司生產t萬件防護服還需投入成本20+9x+50t（萬元）．
  （1）將A公司生產防護服的利潤y（萬元）表示為補貼x（萬元）的函數（政府補貼x萬元計入公司收入）；
  （2）當復工率k=0.8時，政府補貼多少萬元才能使A公司的防護服利潤達到最大？并求出最大值．
  組卷：355引用：7難度：0.5

  解析

• 22．已知函數

  f

  （

  x

  ）

  =

  cosx

  ?

  sin

  （

  x

  +

  π

  3

  ）

  -

  3

  co

  s

  2

  x

  +

  3

  4

  ，

  x

  ∈

  R

  ，
  （1）求f（x）的單調遞減區間；
  （2）求f（x）在閉區間

  [

  -

  π

  4

  ，

  π

  4

  ]

  上的最大值和最小值；
  （3）將函數的圖象f（x）向左平移

  π

  3

  個單位得到函數g（x）的圖象，求函數

  y

  =

  g

  （

  x

  ）

  -

  3

  4

  在[0，2π]上所有零點之和．
  組卷：291引用：5難度：0.7

  解析