當前位置：試卷中心 > 試卷詳情

2020年甘肅省高考數學二診試卷（理科）

發布：2025/11/13 10:0:32

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．一個球的體積和表面積在數值上相等，則該球半徑的數值為（　　）
A．1 B．2 C．3 D．4
組卷：242引用：14難度：0.9
2．設集合A={x|y=lg（3-2x）}，集合B={x|y=
1
-
x
}，則A∩B=（　　）
A．
[
1
，
3
2
）
B．（-∞，1] C．
（
-
∞
，
3
2
]
D．
（
3
2
，
+
∞
）
組卷：70引用：8難度：0.9
3．2022年北京冬奧會首先開賽的是冰壺競賽項目，冰壺（Curling）又稱擲冰壺，冰上溜石，是以隊為單位在冰上進行的一種投擲性競賽項目，被大家喻為冰上的“國際象棋”，它考驗參與者的體能與腦力，展現動靜之美，取舍之智慧．參賽選手只需要將冰壺擲到距離大本營中心最近的圓內就得分，大本營由4個同心圓組成，最大的圓外沿距離圓心為1.829米，第二個半徑為1.219米，第三個半徑為0.610米，最小的半徑為0.1534米，假設某選手等可能地將冰壺投進大本營區域中的任何位置，則他投擲冰壺進入最小圓形區域（以冰壺圓心是否位于圓內作為判斷標準）的概率約為（　　）
A．0.007 B．0.022 C．0.039 D．0.084
組卷：23引用：1難度：0.6
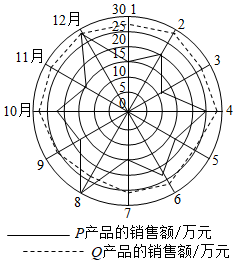4．某商家統計了去年P，Q兩種產品的月銷售額（單位：萬元），繪制了月銷售額的雷達圖，圖中A點表示P產品2月份銷售額約為20萬元，B點表示Q產品9月份銷售額約為25萬元．
根據圖中信息，下面統計結論錯誤的是（　　）
A．P產品的銷售額極差較大
B．P產品銷售額的中位數較大
C．Q產品的銷售額平均值較大
D．Q產品的銷售額波動較小
組卷：114引用：7難度：0.6
5．對實數a和b,定義運算“◎”：a◎b=
a
,
a
-
b
≤
2
b
,
a
-
b
＞
2
，設函數f（x）=（x²-1）◎（5x-x²）（x∈R），若函數y=f（x）-m的圖象與x軸恰有1個公共點，則實數m的取值范圍是（　　）
A．（-1，6] B．
（
-
∞
，-
1
]
∪
（
-
11
4
，
6
）
C．
（
-
11
4
，
+
∞
）
D．
[
-
11
4
，-
1
）
∪
[
6
，
8
]
組卷：156引用：4難度：0.5
6．若一個正四棱錐的左視圖是一個邊長為2的正三角形（如圖），則該正四棱錐的體積是（　　）
A．1 B．
3
C．
4
3
3
D．2
3
組卷：288引用：2難度：0.9
7．已知雙曲線的方程為
x
2
4
-
y
2
3
=
1
，雙曲線右焦點F到雙曲線漸近線的距離為（　　）
A．1 B．
2
C．
3
D．2
組卷：273引用：6難度：0.7
8．已知正六邊形ABCDEF的邊長為2，P是正六邊形ABCDEF邊上任意一點，則
PA
?
PB
的最大值為（　　）
A．13 B．12 C．8 D．
2
3
組卷：557引用：5難度：0.6
9．已知命題p：?x∈R，2023^x+x²⁰²⁴＞0，則p的否定是（　　）
A．?x∈R，2023^x+x²⁰²⁴≤0 B．?x∈R，2023^x+x²⁰²⁴＜0
C．?x∈R，2023^x+x²⁰²⁴≤0 D．?x∈R，2023^x+x²⁰²⁴≠0
組卷：74引用：7難度：0.7
10．設S_n為等差數列{a_n}的前n項和，且?n∈N*，都有
S
n
n
＞
S
n
+
1
n
+
1
，若
a
18
a
17
＜
-
1
，則（　　）
A．S_n的最小值是S₁₇ B．S_n的最小值是S₁₈
C．S_n的最大值是S₁₇ D．S_n的最大值是S₁₈
組卷：121引用：2難度：0.7
11．復數z=cos
π
3
+
isin
π
3
，則在復平面內，復數z²對應的點在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：37引用：4難度：0.9
12．系統找不到該試題

二、填空題：本題共4小題，每小題5分，共20分．

13．已知a∈R，函數f（x）=a?e^x-xlnx的圖像在點（1，f（1））處的切線為直線l,則直線l在y軸上的截距為
．
組卷：6引用：1難度：0.7
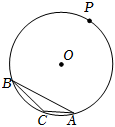14．如圖，P為△ABC外接圓O上一個動點，若CA=1，CB=
3
，∠ACB=150°，則
CA
?
CP
的最大值為
．
組卷：148引用：2難度：0.5
15．函數f（x）=cosx-cos2x的值域為
．
組卷：145引用：1難度：0.7
16．已知函數y=f（x），x∈N^*，f（x）∈N^*，且f（3）＜f（1）＜f（2），若對任意n∈N^*，f（n）+f（n+1）+f（n+2）+f（f（f（n）））=4n+3，則f（2022）=
．
組卷：14引用：2難度：0.5

三、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．第17～21題為必考題，每個試題考生都必須作答．第22、23題為選考題，考生根據要求作答．（一）必考題；共60分．

17．已知拋物線C：y²=2px（p＞0）的焦點為F，準線為l,C上的動點A到點F與到直線x=-2的距離之和的最小值為3．
（1）求C的方程；
（2）過點A作直線交C于另一點B，過點A作C的切線l′，點P在l′上．從下面①②③中選取兩個作為條件，證明另一個成立．
①點P在l上；
②直線PB與C相切；
③點F在直線AB上．
注：若選擇不同的組合分別解答，則按第一個解答計分．
組卷：25引用：1難度：0.5
18．以直角坐標系的原點O為極點，x軸的正半軸為極軸，建立極坐標系，且在兩種坐標系中取相同的長度單位．曲線C的極坐標方程是ρ²=
16
1
+
3
co
s
2
θ
．
（Ⅰ）求曲線C的直角坐標方程；
（Ⅱ）設曲線C與x軸正半軸及y軸正半軸交于點M，N，在第一象限內曲線C上任取一點P，求四邊形OMPN面積的最大值．
組卷：155引用：4難度：0.5
19．已知項數為k（k≥3）的數列{a_n}是各項均為非負實數的遞增數列．若對任意的i,j（1≤i≤j≤k），a_j+a_i與a_j-a_i至少有一個是數列{a_n}中的項，則稱數列{a_n}具有性質?．
（Ⅰ）判斷數列0，1，4，6是否具有性質?，并說明理由；
（Ⅱ）設數列{a_n}具有性質?，求證：2（a₁+a₂+?+a_k-1+a_k）=ka_k；
（Ⅲ）若數列{a_n}具有性質?，且{a_n}不是等差數列，求項數k的所有可能取值．
組卷：92引用：3難度：0.3
20．已知函數f（x）=msinx+
2
cosx,（m＞0）的最大值為2．
（Ⅰ）求函數f（x）在[0，π]上的值域；
（Ⅱ）已知△ABC外接圓半徑R=
3
，f（A-
π
4
）+f（B-
π
4
）=4
6
sinAsinB，角A，B所對的邊分別是a,b,求
1
a
+
1
b
的值．
組卷：170引用：15難度：0.5
21．已知函數f（x）=xlnx,g（x）=2ax²-2x（a＞0）．
（Ⅰ）函數f（x）=xlnx圖像在x=1處的切線與函數g（x）=2ax²-2x相切，求實數a的值；
（Ⅱ）函數f（x）=xlnx與函數g（x）=2ax²-2x圖像有兩個不同交點A（x₁，y₁），B（x₂，y₂）
（ⅰ）求a的取值范圍；
（ⅱ）若
x
2
x
1
≥
2
，證明：
x
1
+
x
2
＞
4
2
e
2
．
組卷：90引用：1難度：0.2

（二）選考題；共10分．請考生在第22、23題中選定一題作答．并用2B鉛筆在答題卡上將所選題目對應的題號方框涂黑．按所涂題號進行評分，不涂、多涂均按所答第一題評分；多答按所答第一題評分．[選修4-4：坐標系與參數方程]（10分）

22．設函數f（x）=|2x+1|-|x-3|
（1）求函數y=f（x）的最小值；
（2）若f（x）≥ax+
a
2
-
7
2
恒成立，求實數a的取值范圍．
組卷：321引用：8難度：0.5

[選修4-5：不等式選講]（10分）

23．如圖，在多面體ABCDEF中，AB∥CD∥EF，EF⊥平面ADE，BE⊥DE
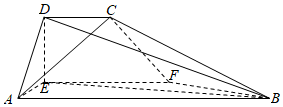
（1）求證：AE⊥CF．
（2）若AB=2EF=4CD=4，AE+DE=2，且直線BD與平面ABFE所成θ的正切值為
17
17
，求二面角A-BC-F的余弦值．
組卷：55引用：1難度：0.5

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2020年甘肅省高考數學二診試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．一個球的體積和表面積在數值上相等，則該球半徑的數值為（　　）

2．設集合A={x|y=lg（3-2x）}，集合B={x|y=
1
-
x
}，則A∩B=（　　）

4．某商家統計了去年P，Q兩種產品的月銷售額（單位：萬元），繪制了月銷售額的雷達圖，圖中A點表示P產品2月份銷售額約為20萬元，B點表示Q產品9月份銷售額約為25萬元．
根據圖中信息，下面統計結論錯誤的是（　　）

5．對實數a和b,定義運算“◎”：a◎b=
a
,
a
-
b
≤
2
b
,
a
-
b
＞
2
，設函數f（x）=（x²-1）◎（5x-x²）（x∈R），若函數y=f（x）-m的圖象與x軸恰有1個公共點，則實數m的取值范圍是（　　）

6．若一個正四棱錐的左視圖是一個邊長為2的正三角形（如圖），則該正四棱錐的體積是（　　）

7．已知雙曲線的方程為
x
2
4
-
y
2
3
=
1
，雙曲線右焦點F到雙曲線漸近線的距離為（　　）

8．已知正六邊形ABCDEF的邊長為2，P是正六邊形ABCDEF邊上任意一點，則
PA
?
PB
的最大值為（　　）

9．已知命題p：?x∈R，2023^x+x²⁰²⁴＞0，則p的否定是（　　）

10．設S_n為等差數列{a_n}的前n項和，且?n∈N*，都有
S
n
n
＞
S
n
+
1
n
+
1
，若
a
18
a
17
＜
-
1
，則（　　）

11．復數z=cos
π
3
+
isin
π
3
，則在復平面內，復數z²對應的點在（　　）

二、填空題：本題共4小題，每小題5分，共20分．

13．已知a∈R，函數f（x）=a?e^x-xlnx的圖像在點（1，f（1））處的切線為直線l,則直線l在y軸上的截距為
．

14．如圖，P為△ABC外接圓O上一個動點，若CA=1，CB=
3
，∠ACB=150°，則
CA
?
CP
的最大值為
．

15．函數f（x）=cosx-cos2x的值域為
．

16．已知函數y=f（x），x∈N^，f（x）∈N^，且f（3）＜f（1）＜f（2），若對任意n∈N^*，f（n）+f（n+1）+f（n+2）+f（f（f（n）））=4n+3，則f（2022）=
．

三、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．第17～21題為必考題，每個試題考生都必須作答．第22、23題為選考題，考生根據要求作答．（一）必考題；共60分．

20．已知函數f（x）=msinx+
2
cosx,（m＞0）的最大值為2．
（Ⅰ）求函數f（x）在[0，π]上的值域；
（Ⅱ）已知△ABC外接圓半徑R=
3
，f（A-
π
4
）+f（B-
π
4
）=4
6
sinAsinB，角A，B所對的邊分別是a,b,求
1
a
+
1
b
的值．

22．設函數f（x）=|2x+1|-|x-3|
（1）求函數y=f（x）的最小值；
（2）若f（x）≥ax+
a
2
-
7
2
恒成立，求實數a的取值范圍．

[選修4-5：不等式選講]（10分）

23．如圖，在多面體ABCDEF中，AB∥CD∥EF，EF⊥平面ADE，BE⊥DE
（1）求證：AE⊥CF．
（2）若AB=2EF=4CD=4，AE+DE=2，且直線BD與平面ABFE所成θ的正切值為
17
17
，求二面角A-BC-F的余弦值．

A．（-1，6]	B．（ - ∞ ，- 1 ] ∪ （ - 11 4 ， 6 ）
C．（ - 11 4 ， + ∞ ）	D． [ - 11 4 ，- 1 ） ∪ [ 6 ， 8 ]

A．?x∈R，2023^x+x²⁰²⁴≤0	B．?x∈R，2023^x+x²⁰²⁴＜0
C．?x∈R，2023^x+x²⁰²⁴≤0	D．?x∈R，2023^x+x²⁰²⁴≠0

A．S_n的最小值是S₁₇	B．S_n的最小值是S₁₈
C．S_n的最大值是S₁₇	D．S_n的最大值是S₁₈

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2020年甘肅省高考數學二診試卷（理科）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的．

1．一個球的體積和表面積在數值上相等，則該球半徑的數值為（ ）

2．設集合A={x|y=lg（3-2x）}，集合B={x|y=1-x}，則A∩B=（ ）

4．某商家統計了去年P，Q兩種產品的月銷售額（單位：萬元），繪制了月銷售額的雷達圖，圖中A點表示P產品2月份銷售額約為20萬元，B點表示Q產品9月份銷售額約為25萬元．根據圖中信息，下面統計結論錯誤的是（ ）

5．對實數a和b,定義運算“◎”：a◎b=a,a-b≤2b,a-b＞2，設函數f（x）=（x2-1）◎（5x-x2）（x∈R），若函數y=f（x）-m的圖象與x軸恰有1個公共點，則實數m的取值范圍是（ ）

6．若一個正四棱錐的左視圖是一個邊長為2的正三角形（如圖），則該正四棱錐的體積是（ ）

7．已知雙曲線的方程為x24-y23=1，雙曲線右焦點F到雙曲線漸近線的距離為（ ）

8．已知正六邊形ABCDEF的邊長為2，P是正六邊形ABCDEF邊上任意一點，則PA?PB的最大值為（ ）

9．已知命題p：?x∈R，2023x+x2024＞0，則p的否定是（ ）

10．設Sn為等差數列{an}的前n項和，且?n∈N*，都有Snn＞Sn+1n+1，若a18a17＜-1，則（ ）

11．復數z=cosπ3+isinπ3，則在復平面內，復數z2對應的點在（ ）

二、填空題：本題共4小題，每小題5分，共20分．

13．已知a∈R，函數f（x）=a?ex-xlnx的圖像在點（1，f（1））處的切線為直線l,則直線l在y軸上的截距為．

14．如圖，P為△ABC外接圓O上一個動點，若CA=1，CB=3，∠ACB=150°，則CA?CP的最大值為 ．

15．函數f（x）=cosx-cos2x的值域為 ．

16．已知函數y=f（x），x∈N*，f（x）∈N*，且f（3）＜f（1）＜f（2），若對任意n∈N*，f（n）+f（n+1）+f（n+2）+f（f（f（n）））=4n+3，則f（2022）=．

三、解答題：共70分．解答應寫出文字說明、證明過程或演算步驟．第17～21題為必考題，每個試題考生都必須作答．第22、23題為選考題，考生根據要求作答．（一）必考題；共60分．

20．已知函數f（x）=msinx+2cosx,（m＞0）的最大值為2．（Ⅰ）求函數f（x）在[0，π]上的值域；（Ⅱ）已知△ABC外接圓半徑R=3，f（A-π4）+f（B-π4）=46sinAsinB，角A，B所對的邊分別是a,b,求1a+1b的值．

22．設函數f（x）=|2x+1|-|x-3|（1）求函數y=f（x）的最小值；（2）若f（x）≥ax+a2-72恒成立，求實數a的取值范圍．

[選修4-5：不等式選講]（10分）

23．如圖，在多面體ABCDEF中，AB∥CD∥EF，EF⊥平面ADE，BE⊥DE（1）求證：AE⊥CF．（2）若AB=2EF=4CD=4，AE+DE=2，且直線BD與平面ABFE所成θ的正切值為1717，求二面角A-BC-F的余弦值．

1．一個球的體積和表面積在數值上相等，則該球半徑的數值為（　　）

2．設集合A={x|y=lg（3-2x）}，集合B={x|y=
1
-
x
}，則A∩B=（　　）

4．某商家統計了去年P，Q兩種產品的月銷售額（單位：萬元），繪制了月銷售額的雷達圖，圖中A點表示P產品2月份銷售額約為20萬元，B點表示Q產品9月份銷售額約為25萬元．
根據圖中信息，下面統計結論錯誤的是（　　）

5．對實數a和b,定義運算“◎”：a◎b=
a
,
a
-
b
≤
2
b
,
a
-
b
＞
2
，設函數f（x）=（x²-1）◎（5x-x²）（x∈R），若函數y=f（x）-m的圖象與x軸恰有1個公共點，則實數m的取值范圍是（　　）

6．若一個正四棱錐的左視圖是一個邊長為2的正三角形（如圖），則該正四棱錐的體積是（　　）

7．已知雙曲線的方程為
x
2
4
-
y
2
3
=
1
，雙曲線右焦點F到雙曲線漸近線的距離為（　　）

8．已知正六邊形ABCDEF的邊長為2，P是正六邊形ABCDEF邊上任意一點，則
PA
?
PB
的最大值為（　　）

9．已知命題p：?x∈R，2023^x+x²⁰²⁴＞0，則p的否定是（　　）

10．設S_n為等差數列{a_n}的前n項和，且?n∈N*，都有
S
n
n
＞
S
n
+
1
n
+
1
，若
a
18
a
17
＜
-
1
，則（　　）

11．復數z=cos
π
3
+
isin
π
3
，則在復平面內，復數z²對應的點在（　　）

13．已知a∈R，函數f（x）=a?e^x-xlnx的圖像在點（1，f（1））處的切線為直線l,則直線l在y軸上的截距為
．

14．如圖，P為△ABC外接圓O上一個動點，若CA=1，CB=
3
，∠ACB=150°，則
CA
?
CP
的最大值為
．

15．函數f（x）=cosx-cos2x的值域為
．

16．已知函數y=f（x），x∈N^，f（x）∈N^，且f（3）＜f（1）＜f（2），若對任意n∈N^*，f（n）+f（n+1）+f（n+2）+f（f（f（n）））=4n+3，則f（2022）=
．

20．已知函數f（x）=msinx+
2
cosx,（m＞0）的最大值為2．
（Ⅰ）求函數f（x）在[0，π]上的值域；
（Ⅱ）已知△ABC外接圓半徑R=
3
，f（A-
π
4
）+f（B-
π
4
）=4
6
sinAsinB，角A，B所對的邊分別是a,b,求
1
a
+
1
b
的值．

22．設函數f（x）=|2x+1|-|x-3|
（1）求函數y=f（x）的最小值；
（2）若f（x）≥ax+
a
2
-
7
2
恒成立，求實數a的取值范圍．

23．如圖，在多面體ABCDEF中，AB∥CD∥EF，EF⊥平面ADE，BE⊥DE
（1）求證：AE⊥CF．
（2）若AB=2EF=4CD=4，AE+DE=2，且直線BD與平面ABFE所成θ的正切值為
17
17
，求二面角A-BC-F的余弦值．