當前位置：試卷中心 > 試卷詳情

2020年江蘇省南通市高考數學學科基地密卷（六）

發布：2025/11/13 10:0:32

一、填空題：本大題共14小題，每小題5分，共70分.

1．方程x²+2x+3=0在復數范圍內的根為
．
組卷：41引用：2難度：0.8
2．函數
f
（
x
）
=
3
sin
（
2
x
+
π
4
）
，x∈R的單調遞減區間是
．
組卷：189引用：2難度：0.7
3．已知全集U={1，2，3，4}，集合A={1，4}，則?_UA=
．
組卷：57引用：2難度：0.8
4．若函數f（x）=lnx-x-mx在區間[1，e²]內有唯一的零點，則實數m的取值范圍是

．
組卷：99引用：3難度：0.5
5．設
a
=（1，0，-1），
b
=（-1，1，1），則（
a
+
b
）?（-2
b
）=
．
組卷：0引用：0難度：0.8
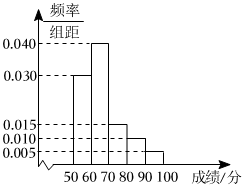6．在某中學舉行的環保知識競賽中，將三個年級參賽學生的成績進行整理后分成5組，繪制出如圖所示的頻率分布直方圖，圖中從左到右依次為第一、第二、第三、第四、第五小組．已知第二小組的頻數是40，則成績在80-100分的學生人數是
．
組卷：9引用：6難度：0.7
7．五一長假期間，某單位安排A，B，C這3人在5天假期值班，每天只需1人值班，且每人至少值班1天，已知A在五一長假期間值班2天，則A連續值班的概率是
．
組卷：25引用：3難度：0.7
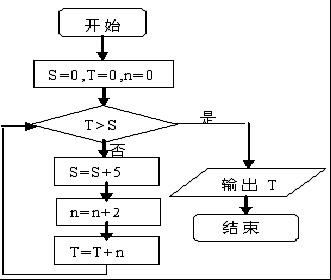8．執行如圖的程序框圖，輸出的T=
．
組卷：174引用：4難度：0.7
9．圓心在第二象限，半徑為3，且與兩條坐標軸均相切的圓的標準方程為
．
組卷：81引用：2難度：0.7
10．已知x＞5，則
x
+
1
x
-
5
的最小值是
．
組卷：52引用：4難度：0.7
11．等比數列{a_n}的前3項分別為x,3x+3，6x+6，則a₄=
．
組卷：159引用：3難度：0.8
12．過拋物線y²=4x的焦點，引傾斜角為60°的直線，交拋物線于A、B兩點，則△OAB的面積為

．
組卷：29引用：1難度：0.5
13．已知奇函數y=f（x）的周期為2，且當x∈（0，1）時，f（x）=log₂x.則f（7.5）的值為
組卷：325引用：3難度：0.7
14．已知球O的直徑長為12，當它的內接正四棱錐的體積最大時，該四棱錐的高為

．
組卷：79引用：2難度：0.5

二、解答題：本大題共6小題，共計90分.解答時應寫出文字說明、證明過程或演算步驟.

15．某同學在探究直線與橢圓的位置關系時發現橢圓的一個重要性質：橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
在任意一點M（x₀，y₀）處的切線方程為
x
x
0
a
2
+
y
y
0
b
2
=
1
．現給定橢圓
C
：
x
2
4
+
y
2
3
=
1
，過C的右焦點F的直線l交橢圓C于P，Q兩點，過P，Q分別作C的兩條切線，兩切線相交于點G．
（1）求點G的軌跡方程；
（2）若過點F且與直線l垂直的直線（斜率存在且不為零）交橢圓C于M，N兩點，證明：
1
|
PQ
|
+
1
|
MN
|
為定值．
組卷：72引用：3難度：0.4
16．已知函數f（x）=e^x+ax（a∈R），g（x）=ln（x+1）．
（1）當a=1時，求函數f（x）在點（0，1）處的切線；
（2）若f（x）≥1-g（x）對任意的x∈[0，+∞）恒成立，求實數a的取值范圍；
（3）求證：x＞0時，（e^x-1）g（x）＞x²．
組卷：328引用：2難度：0.3
17．圖①是由矩形ADEB，Rt△ABC和菱形BFGC組成的一個平面圖形，其中AB=1，BE=BF=2，∠FBC=60°．將其沿AB，BC折起使得BE與BF重合，連接DG，如圖②．在圖②中解決下列問題：

（1）證明：AB⊥平面BCGE；
（2）證明：四邊形ACGD是平行四邊形；
（3）求四邊形ACGD的面積．
組卷：17引用：2難度：0.6
18．袋中裝有4個大小相同的小球，編號為1，2，3，4，現從袋中有放回地取球2次．
（1）求2次都取得3號球的概率；
（2）記這兩次取得球的號碼的最大值為X，求X的分布列．
組卷：438引用：4難度：0.6
19．數列A：a₁，a₂，…，a_m（m≥2）與B：b₁，b₂，…，b_n（n≥2）均為遞增正整數數列．若對于B中任意一項b_i，A中存在唯一的一對（a_j，a_k），滿足b_i=a_j-a_k，則稱B可以由A生成，記為A→B．
（1）若A：1，2，3，6，B₁：1，2，B₂：2，3，B₃：1，2，3，4，5，B₄：2，3，4，5，直接寫出B₁，B₂，B₃，B₄中可以由A生成的數列；
（2）若A：1，a₂，a₃，a₄，B：1，2，3，4，5，6，求所有滿足條件A→B的數列A；
（3）證明：對于任意數列B，一定存在數列A，滿足A→B．
組卷：15引用：2難度：0.5
20．（選修4-2：矩陣與變換）
已知矩陣A的逆矩陣A^-1=
1
0
0
2
，求矩陣A．
組卷：26引用：3難度：0.3

【選做題】本題包括A、B、C三小題，請選定其中兩題，并在相應的答題區域內作答.A.[選修4-2：矩陣與變換]

21．已知向量
a
=
（
1
，
2
）
，
b
=
（
3
，
x
）
，
c
=
（
2
，
y
）
，且
a
∥
b
，
a
⊥
c
．
（1）求
b
與
c
；
（2）若
m
=2
a
-
b
，
n
=
a
+
c
，求向量
m
，
n
的夾角的大小．
組卷：36引用：2難度：0.7

B.[選修4-4：坐標系與參數方程]

22．某地區上年度居民生活水價為2.8元/m³，年用水量為am³，本年度計劃將水價降到2.3元/m³到2.6元/m³之間，而用戶期望水價為2元/m³．經測算，下調水價后新增用水量和實際水價與用戶的期望水價的差成反比（比例系數為k），已知該地區的水價成本價為1.8元/m³
（1）寫出本年度水價下調后水務部門的收益y（單位：元）關于實際水價x（單位：元/m³）的函數解析式；（收益=實際水量×（實際水價-成本價））
（2）設k=0.4a,當水價最低定為多少時，仍可保證水務部門的收益比上年至少增長20%？
（3）設k=0.8a,當水價定為多少時，本年度水務部門的收益最低？并求出最低收益．
組卷：20引用：2難度：0.6

C.[選修4-5：不等式選講]

23．已知O為坐標原點，拋物線C：y²=2px（0＜p＜2）上一點
P
（
1
p
，
2
）
到拋物線焦點的距離為
3
2
，若過點M（2，0）的直線l與拋物線C：y²=2px交于A，B兩點．
（1）證明：OA⊥OB；
（2）若l與坐標軸不平行，且A關于x軸的對稱點為D，圓N：x²+y²+4x-2y+3=0，證明：直線BD恒與圓N相交．
組卷：48引用：2難度：0.6

【必做題】第22題、第23題，每題10分，共計20分，請在答卷紙指定區域內作答.

24．已知函數
f
（
x
）
=
lo
g
1
2
（
x
2
+
1
）
，g（x）=x²-ax+6．
（1）若關于x的不等式g（x）＜0的解集為{x|2＜x＜3}，求函數y=
g
（
x
）
x
-
1
（x＞1）的最小值；
（2）是否存在實數a,使得對任意x₁∈[-2，4]，存在x₂∈[1，+∞），不等式g（x₁）＜f（x₂）成立？若存在求出a的取值范圍，若不存在，說明理由．
組卷：163引用：1難度：0.5
25．在平面直角坐標系xOy中，以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，已知在極坐標系中，A（3
3
，
π
2
），B（3，
π
3
），圓C的方程為ρ=2cosθ．
（1）求在平面直角坐標系xOy中圓C的標準方程；
（2）已知P為圓C上的任意一點，求△ABP面積的最大值．
組卷：110引用：12難度：0.3

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2020年江蘇省南通市高考數學學科基地密卷（六）

一、填空題：本大題共14小題，每小題5分，共70分.

1．方程x2+2x+3=0在復數范圍內的根為 ．

2．函數f（x）=3sin（2x+π4），x∈R的單調遞減區間是 ．

3．已知全集U={1，2，3，4}，集合A={1，4}，則?UA=．

4．若函數f（x）=lnx-x-mx在區間[1，e2]內有唯一的零點，則實數m的取值范圍是 ．

5．設a=（1，0，-1），b=（-1，1，1），則（a+b）?（-2b）=．

7．五一長假期間，某單位安排A，B，C這3人在5天假期值班，每天只需1人值班，且每人至少值班1天，已知A在五一長假期間值班2天，則A連續值班的概率是 ．

8．執行如圖的程序框圖，輸出的T=．

9．圓心在第二象限，半徑為3，且與兩條坐標軸均相切的圓的標準方程為 ．

10．已知x＞5，則x+1x-5的最小值是 ．

11．等比數列{an}的前3項分別為x,3x+3，6x+6，則a4=．

12．過拋物線y2=4x的焦點，引傾斜角為60°的直線，交拋物線于A、B兩點，則△OAB的面積為 ．

13．已知奇函數y=f（x）的周期為2，且當x∈（0，1）時，f（x）=log2x.則f（7.5）的值為

14．已知球O的直徑長為12，當它的內接正四棱錐的體積最大時，該四棱錐的高為 ．

二、解答題：本大題共6小題，共計90分.解答時應寫出文字說明、證明過程或演算步驟.

16．已知函數f（x）=ex+ax（a∈R），g（x）=ln（x+1）．（1）當a=1時，求函數f（x）在點（0，1）處的切線；（2）若f（x）≥1-g（x）對任意的x∈[0，+∞）恒成立，求實數a的取值范圍；（3）求證：x＞0時，（ex-1）g（x）＞x2．

18．袋中裝有4個大小相同的小球，編號為1，2，3，4，現從袋中有放回地取球2次．（1）求2次都取得3號球的概率；（2）記這兩次取得球的號碼的最大值為X，求X的分布列．

20．（選修4-2：矩陣與變換）已知矩陣A的逆矩陣A-1=1002，求矩陣A．

【選做題】本題包括A、B、C三小題，請選定其中兩題，并在相應的答題區域內作答.A.[選修4-2：矩陣與變換]

21．已知向量a=（1，2），b=（3，x），c=（2，y），且a∥b，a⊥c．（1）求b與c；（2）若m=2a-b，n=a+c，求向量m，n的夾角的大小．

B.[選修4-4：坐標系與參數方程]

C.[選修4-5：不等式選講]

【必做題】第22題、第23題，每題10分，共計20分，請在答卷紙指定區域內作答.

1．方程x²+2x+3=0在復數范圍內的根為
．

2．函數
f
（
x
）
=
3
sin
（
2
x
+
π
4
）
，x∈R的單調遞減區間是
．

3．已知全集U={1，2，3，4}，集合A={1，4}，則?_UA=
．

4．若函數f（x）=lnx-x-mx在區間[1，e²]內有唯一的零點，則實數m的取值范圍是

．

5．設
a
=（1，0，-1），
b
=（-1，1，1），則（
a
+
b
）?（-2
b
）=
．

7．五一長假期間，某單位安排A，B，C這3人在5天假期值班，每天只需1人值班，且每人至少值班1天，已知A在五一長假期間值班2天，則A連續值班的概率是
．

8．執行如圖的程序框圖，輸出的T=
．

9．圓心在第二象限，半徑為3，且與兩條坐標軸均相切的圓的標準方程為
．

10．已知x＞5，則
x
+
1
x
-
5
的最小值是
．

11．等比數列{a_n}的前3項分別為x,3x+3，6x+6，則a₄=
．

12．過拋物線y²=4x的焦點，引傾斜角為60°的直線，交拋物線于A、B兩點，則△OAB的面積為

．

13．已知奇函數y=f（x）的周期為2，且當x∈（0，1）時，f（x）=log₂x.則f（7.5）的值為

14．已知球O的直徑長為12，當它的內接正四棱錐的體積最大時，該四棱錐的高為

．

16．已知函數f（x）=e^x+ax（a∈R），g（x）=ln（x+1）．
（1）當a=1時，求函數f（x）在點（0，1）處的切線；
（2）若f（x）≥1-g（x）對任意的x∈[0，+∞）恒成立，求實數a的取值范圍；
（3）求證：x＞0時，（e^x-1）g（x）＞x²．

18．袋中裝有4個大小相同的小球，編號為1，2，3，4，現從袋中有放回地取球2次．
（1）求2次都取得3號球的概率；
（2）記這兩次取得球的號碼的最大值為X，求X的分布列．

20．（選修4-2：矩陣與變換）
已知矩陣A的逆矩陣A^-1=
1
0
0
2
，求矩陣A．

21．已知向量
a
=
（
1
，
2
）
，
b
=
（
3
，
x
）
，
c
=
（
2
，
y
）
，且
a
∥
b
，
a
⊥
c
．
（1）求
b
與
c
；
（2）若
m
=2
a
-
b
，
n
=
a
+
c
，求向量
m
，
n
的夾角的大小．