當前位置：試卷中心 > 試卷詳情

2020年江西省九江市高考數學一模試卷（文科）

發布：2025/11/13 11:0:31

一、選擇題：本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的.

1．設集合M={x|0＜x＜3}，N={x|
1
2
≤x≤4}，則M∩N等于（　　）
A．
{
x
|
0
＜
x
≤
1
2
}
B．
{
x
|
1
2
≤
x
＜
3
}
C．{x|3≤x＜4} D．{x|0＜x≤4}
組卷：67引用：5難度：0.9
2．已知變量x,y滿足約束條件
x
+
y
-
6
≤
0
x
-
3
y
+
2
≤
0
x
≥
1
，則目標函數z=x+2y的最小值為（　　）
A．11 B．3 C．1 D．8
組卷：17引用：1難度：0.6
3．已知函數
f
（
x
）
=
2
sin
（
ωx
+
φ
）
（
ω
＞
0
，-
π
2
＜
φ
＜
π
2
）
圖象的相鄰兩條對稱軸之間的距離為
π
6
，且關于點
（
5
π
18
，
0
）
對稱，則φ的值為（　　）
A．
π
12
B．
π
6
C．
π
4
D．
π
3
組卷：218引用：4難度：0.5
4．已知函數f（x）=x²+x-1的定義域為R，f（x）可以表示為一個偶函數g（x）和一個奇函數h（x）之和，若不等式
g
（
kx
+
k
x
）
＜
g
（
x
2
+
1
x
2
+
1
）
對任意非零實數x恒成立，則實數k的取值范圍為（　　）
A．
（
-
3
2
，
3
2
）
B．
（
-
3
2
，
0
]
C．
（
-
∞
，-
3
2
）
∪
（
3
2
，
+
∞
）
D．
（
-
3
2
，
0
）
∪
（
0
，
3
2
）
組卷：77引用：3難度：0.5
5．已知i為虛數單位，則復數-2+3i在復平面內對應的點在（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
組卷：7引用：3難度：0.8
6．某籃球隊甲、乙兩名運動員練習罰球，每人練習10組，每組罰球40個．命中個數的莖葉圖如圖，則下面結論中錯誤的一個是（　　）
A．甲的極差是29 B．乙的眾數是21
C．甲罰球命中率比乙高 D．甲的中位數是24
組卷：193引用：35難度：0.9
7．連結橢圓
x
2
a
2
+
y
2
=
1
（
a
＞
1
）
短軸的一個頂點與兩個焦點組成正三角形，則橢圓的準線方程為（　　）
A．
x
=±
4
3
3
B．
x
=±
2
3
3
C．
y
=±
4
3
3
D．
y
=±
2
3
3
組卷：13引用：1難度：0.9
8．已知函數f（x）的定義域為R，f（2x-2）為偶函數，f（x-3）+f（-x+1）=0，當x∈[-2，-1]時，
f
（
x
）
=
1
a
x
-
ax
-
4
（a＞0且a≠1），且f（-2）=4．則
19
∑
k
=
1
|
f
（
k
）
|
=（　　）
A．28 B．32 C．36 D．40
組卷：436引用：7難度：0.5
9．設a∈R，則“a²＞a”是“a＞1”的（　　）
A．充分不必要條件 B．充要條件
C．必要不充分條件 D．既不充分也不必要條件
組卷：129引用：3難度：0.8
10．已知等差數列{a_n}的前n項和為S_n，a₃=4，S₇=56，則a₇=（　　）
A．10 B．12 C．16 D．20
組卷：291引用：3難度：0.8
11．甲同學參加青年志愿者的選拔，選拔以現場答題的方式進行．已知在備選的8道試題中，甲能答對其中的4道題，規定每次考試都從備選題中隨機抽出4道題進行測試．設甲答對的試題數為X，則X=3的概率為（　　）
A．
6
35
B．
2
7
C．
9
35
D．
8
35
組卷：49引用：7難度：0.8
12．劉徽在他的《九章算術注》中提出一個獨特的方法來計算球體的體積：他不直接給出球體的體積，而是先計算另一個叫“牟合方蓋”的立體的體積．劉徽通過計算，“牟合方蓋”的體積與球的體積之比應為
4
π
．后人導出了“牟合方蓋”的
1
8
體積計算公式，即
1
8
V_牟=r³-V_方蓋差，r為球的半徑，也即正方體的棱長均為2r,為從而計算出V_球=
4
3
πr³．記所有棱長都為r的正四棱錐的體積為V_正，棱長為2r的正方體的方蓋差為V_方蓋差，則
V
方蓋差
V
正
=（　　）
A．
1
2
B．
2
2
C．
2
D．
3
組卷：198引用：2難度：0.5

二、填空題：本大題共4小題，每小題5分，共20分.

13．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，點P是C的右支上一點，連接PF₁與y軸交于點M，若|F₁O|=3|OM|（O為坐標原點），PF₁⊥PF₂，則雙曲線C的離心率為
．
組卷：63引用：2難度：0.5
14．閱讀如圖所示的程序框圖輸出的S是
．
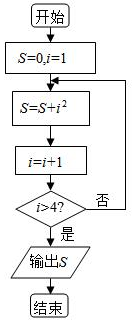組卷：16引用：5難度：0.7
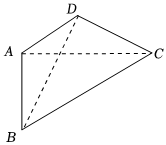15．在平面四邊形ABCD中，AB⊥AC，
AC
=
3
AB
，AD=CD=1，則BD的最大值為
．
組卷：143引用：3難度：0.5
16．函數y=sinx的圖象在點（π，0）處的切線方程為

．
組卷：49引用：5難度：0.9

三、解答題：本大題共5小題，共70分．解答應寫出文字說明，證明過程或演算步驟.

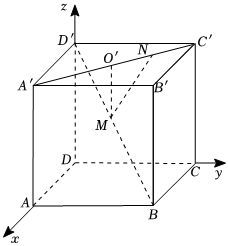17．如圖，已知正方體ABCD-A′B′C′D′的棱長為a,M為BD′的中點，點N在A′C′上，且|A′N|=3|NC′|，試求MN的長．
組卷：88引用：6難度：0.5
18．（1）已知a,b,c,d∈R求證：（a²+b²）（c²+d²）≥（ac+bd）²；
（2）?a,b,c＞0，a+b+c=3，求證：a²+b²+c²≥3．
組卷：12引用：2難度：0.5
19．在直角坐標系xOy中，以O為極點，x軸的正半軸為極軸建立極坐標系，已知直線l的參數方程為
x
=
-
1
+
t
y
=
1
+
t
，（t為參數），曲線C的普通方程為（x-2）²+（y-1）²=5，點P的極坐標為（2
2
，
7
π
4
）．
（1）求直線l的普通方程和曲線C的極坐標方程；
（2）若將直線l向右平移2個單位得到直線l′，設l′與C相交于A，B兩點，求△PAB的面積．
組卷：93引用：9難度：0.5

20．在隧道施工過程中，若隧道拱頂下沉速率過快，無法保證工程施工的安全性，則需及時調整支護參數．某施工隊對正在施工的福州象山隧道工程進行下沉量監控，通過對監控結果進行回歸分析，建立前t天隧道拱頂的累加總下沉量z（單位：毫米）與時間t（單位：天）的回歸方程，通過回歸方程預測是否需要調整支護參數．已知該隧道拱頂下沉的實測數據如表所示：

t（單位：天） 1 2 3 4 5 6 7

z（單位：毫米） 0.01 0.04 0.14 0.52 1.38 2.31 4.30

研究人員制作相應散點圖，通過觀察，擬用函數z=ke^bt進行擬合．令u=lnz,計算得：
z
=
1
.
2
，
7
∑
i
=
1
（
t
i
-
t
）
（
z
i
-
z
）
=
22
.
3
，
7
∑
i
=
1
（
z
i
-
z
）
2
=
27
.
5
，
u
=
-
1
.
2
，
7
∑
i
=
1
（
t
i
-
t
）
（
u
i
-
u
）
=
25
.
2
，
7
∑
i
=
1
（
u
i
-
u
）
2
=
30
．
（1）試建立z與t的回歸方程，并預測前8天該隧道拱頂的累加總下沉量；（精確到0.1）
（2）已知當拱頂在某個時刻下沉的瞬時速率超過27毫米/天時，支護系統將超負荷，隧道有塌方風險，施工隊需要提前一天調整支護參數、試估計最遲在第幾天調整支護參數？（精確到整數）
附：①回歸直線
?
y
=
?
a
+
?
b
x
中斜率和截距的最小二乘估計公式分別為：
?
b
=
n
∑
i
=
1
（
x
i
-
x
）
（
y
i
-
y
）
n
∑
i
=
1
（
x
i
-
x
）
2
，
?
a
=
y
-
?
b
x
；
②參考數據：
210
≈
14
.
5
，
ln
10
≈
2
.
3
，
ln
30
≈
3
.
4
，
e
2
.
4
≈
11
.
0
，
e
2
≈
7
.
38
．

組卷：3引用：3難度：0.6

21．已知拋物線C：y²=2px（p＞0）的焦點為F，M（1，y₀）（y₀＞0）是拋物線上一點且三角形MOF的面積為
1
8
（其中O為坐標原點），不過點M的直線l與拋物線C交于P，Q兩點，且以PQ為直徑的圓經過點M，過點M作MN⊥PQ交PQ于點N．
（1）求拋物線C的方程；
（2）求證直線PQ恒過定點，并求出點N的軌跡方程．
組卷：148引用：3難度：0.6

請考生在第22-23題中任選一題作答，如果多做，則按所做的第一題計分.[選修4-4：坐標系與參數方程]

22．在各項均為正數的等比數列{a_n}中，a₂=1，且2a₃，a₅，3a₄成等差數列．
（Ⅰ）求數列{a_n}的通項公式；
（Ⅱ）若數列{b_n}滿足b_n=2log₂a_n+1，S_n為數列{b_n}的前n項和．設c_n=
S
n
-
4
n
n
a
n
，當c_n最大時，求n的值．
組卷：54引用：2難度：0.5

[選修4-5：不等式選講]

23．已知函數
f
（
x
）
=
-
x
3
+
x
2
，
x
＜
1
alnx
,

x
≥
1
.

（Ⅰ）求f（x）在[-1，e]（e為自然對數的底數）上的最大值；
（Ⅱ）對任意給定的正實數a,曲線y=f（x）上是否存在兩點P，Q，使得POQ是以O為直角頂點的直角三角形，且此三角形斜邊中點在y軸上？
組卷：22引用：5難度：0.3

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（ - 3 2 ， 3 2 ）	B．（ - 3 2 ， 0 ]
C．（ - ∞ ，- 3 2 ） ∪ （ 3 2 ， + ∞ ）	D．（ - 3 2 ， 0 ） ∪ （ 0 ， 3 2 ）

A．甲的極差是29	B．乙的眾數是21
C．甲罰球命中率比乙高	D．甲的中位數是24

A．充分不必要條件	B．充要條件
C．必要不充分條件	D．既不充分也不必要條件

t（單位：天）	1	2	3	4	5	6	7
z（單位：毫米）	0.01	0.04	0.14	0.52	1.38	2.31	4.30

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2020年江西省九江市高考數學一模試卷（文科）

一、選擇題：本大題共12小題，每小題5分，共60分．在每小題給出的四個選項中，只有一項是符合題目要求的.

1．設集合M={x|0＜x＜3}，N={x|12≤x≤4}，則M∩N等于（ ）

2．已知變量x,y滿足約束條件x+y-6≤0x-3y+2≤0x≥1，則目標函數z=x+2y的最小值為（ ）

3．已知函數f（x）=2sin（ωx+φ）（ω＞0，-π2＜φ＜π2）圖象的相鄰兩條對稱軸之間的距離為π6，且關于點（5π18，0）對稱，則φ的值為（ ）

4．已知函數f（x）=x2+x-1的定義域為R，f（x）可以表示為一個偶函數g（x）和一個奇函數h（x）之和，若不等式g（kx+kx）＜g（x2+1x2+1）對任意非零實數x恒成立，則實數k的取值范圍為（ ）

5．已知i為虛數單位，則復數-2+3i在復平面內對應的點在（ ）

6．某籃球隊甲、乙兩名運動員練習罰球，每人練習10組，每組罰球40個．命中個數的莖葉圖如圖，則下面結論中錯誤的一個是（ ）

7．連結橢圓x2a2+y2=1（a＞1）短軸的一個頂點與兩個焦點組成正三角形，則橢圓的準線方程為（ ）

8．已知函數f（x）的定義域為R，f（2x-2）為偶函數，f（x-3）+f（-x+1）=0，當x∈[-2，-1]時，f（x）=1ax-ax-4（a＞0且a≠1），且f（-2）=4．則19∑k=1|f（k）|=（ ）

9．設a∈R，則“a2＞a”是“a＞1”的（ ）

10．已知等差數列{an}的前n項和為Sn，a3=4，S7=56，則a7=（ ）

11．甲同學參加青年志愿者的選拔，選拔以現場答題的方式進行．已知在備選的8道試題中，甲能答對其中的4道題，規定每次考試都從備選題中隨機抽出4道題進行測試．設甲答對的試題數為X，則X=3的概率為（ ）

二、填空題：本大題共4小題，每小題5分，共20分.

13．已知雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左、右焦點分別為F1，F2，點P是C的右支上一點，連接PF1與y軸交于點M，若|F1O|=3|OM|（O為坐標原點），PF1⊥PF2，則雙曲線C的離心率為 ．

14．閱讀如圖所示的程序框圖輸出的S是．

15．在平面四邊形ABCD中，AB⊥AC，AC=3AB，AD=CD=1，則BD的最大值為 ．

16．函數y=sinx的圖象在點（π，0）處的切線方程為 ．

三、解答題：本大題共5小題，共70分．解答應寫出文字說明，證明過程或演算步驟.

17．如圖，已知正方體ABCD-A′B′C′D′的棱長為a,M為BD′的中點，點N在A′C′上，且|A′N|=3|NC′|，試求MN的長．

18．（1）已知a,b,c,d∈R求證：（a2+b2）（c2+d2）≥（ac+bd）2；（2）?a,b,c＞0，a+b+c=3，求證：a2+b2+c2≥3．

請考生在第22-23題中任選一題作答，如果多做，則按所做的第一題計分.[選修4-4：坐標系與參數方程]

22．在各項均為正數的等比數列{an}中，a2=1，且2a3，a5，3a4成等差數列．（Ⅰ）求數列{an}的通項公式；（Ⅱ）若數列{bn}滿足bn=2log2an+1，Sn為數列{bn}的前n項和．設cn=Sn-4nnan，當cn最大時，求n的值．

[選修4-5：不等式選講]

1．設集合M={x|0＜x＜3}，N={x|
1
2
≤x≤4}，則M∩N等于（　　）

2．已知變量x,y滿足約束條件
x
+
y
-
6
≤
0
x
-
3
y
+
2
≤
0
x
≥
1
，則目標函數z=x+2y的最小值為（　　）

3．已知函數
f
（
x
）
=
2
sin
（
ωx
+
φ
）
（
ω
＞
0
，-
π
2
＜
φ
＜
π
2
）
圖象的相鄰兩條對稱軸之間的距離為
π
6
，且關于點
（
5
π
18
，
0
）
對稱，則φ的值為（　　）

4．已知函數f（x）=x²+x-1的定義域為R，f（x）可以表示為一個偶函數g（x）和一個奇函數h（x）之和，若不等式
g
（
kx
+
k
x
）
＜
g
（
x
2
+
1
x
2
+
1
）
對任意非零實數x恒成立，則實數k的取值范圍為（　　）

5．已知i為虛數單位，則復數-2+3i在復平面內對應的點在（　　）

6．某籃球隊甲、乙兩名運動員練習罰球，每人練習10組，每組罰球40個．命中個數的莖葉圖如圖，則下面結論中錯誤的一個是（　　）

7．連結橢圓
x
2
a
2
+
y
2
=
1
（
a
＞
1
）
短軸的一個頂點與兩個焦點組成正三角形，則橢圓的準線方程為（　　）

8．已知函數f（x）的定義域為R，f（2x-2）為偶函數，f（x-3）+f（-x+1）=0，當x∈[-2，-1]時，
f
（
x
）
=
1
a
x
-
ax
-
4
（a＞0且a≠1），且f（-2）=4．則
19
∑
k
=
1
|
f
（
k
）
|
=（　　）

9．設a∈R，則“a²＞a”是“a＞1”的（　　）

10．已知等差數列{a_n}的前n項和為S_n，a₃=4，S₇=56，則a₇=（　　）

11．甲同學參加青年志愿者的選拔，選拔以現場答題的方式進行．已知在備選的8道試題中，甲能答對其中的4道題，規定每次考試都從備選題中隨機抽出4道題進行測試．設甲答對的試題數為X，則X=3的概率為（　　）

13．已知雙曲線
C
：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，點P是C的右支上一點，連接PF₁與y軸交于點M，若|F₁O|=3|OM|（O為坐標原點），PF₁⊥PF₂，則雙曲線C的離心率為
．

14．閱讀如圖所示的程序框圖輸出的S是
．

15．在平面四邊形ABCD中，AB⊥AC，
AC
=
3
AB
，AD=CD=1，則BD的最大值為
．

16．函數y=sinx的圖象在點（π，0）處的切線方程為

．

18．（1）已知a,b,c,d∈R求證：（a²+b²）（c²+d²）≥（ac+bd）²；
（2）?a,b,c＞0，a+b+c=3，求證：a²+b²+c²≥3．

22．在各項均為正數的等比數列{a_n}中，a₂=1，且2a₃，a₅，3a₄成等差數列．
（Ⅰ）求數列{a_n}的通項公式；
（Ⅱ）若數列{b_n}滿足b_n=2log₂a_n+1，S_n為數列{b_n}的前n項和．設c_n=
S
n
-
4
n
n
a
n
，當c_n最大時，求n的值．