2021-2022學年湖北省宜昌英杰學校高三（上）月考數學試卷（10月份）

一、選擇題（本大題共8小題，共40.0分）

• 1．已知圖甲為函數y=f（x）的圖象，則圖乙中的圖象對應的函數可能為（　　）

  A．y=|f（x）|

  B．y=f（|x|）

  C．y=f（-|x|）

  D．y=-f（-|x|）
  組卷：106引用：2難度：0.7

  解析

• 2．已知集合A={y|y=2^x，x≥0}，B={x∈N||2x-3|≤1}，則A∩B=（　　）

  A．{0，1，2}

  B．{1，2}

  C．{1，2，3}

  D．{2，3}
  組卷：24引用：4難度：0.9

  解析

• 3．已知圓錐的頂點和底面圓周均在球O的球面上，若該圓錐的底面半徑為

  2

  3

  ，高為6，則球O的表面積為（　　）

  A．80π

  B．64π

  C．48π

  D．32π
  組卷：544引用：1難度：0.7

  解析

• 4．已知全集U={1，2，3，4，5}，集合A={3，4，5}，B={2，3，4}，則?_U（A∩B）=（　　）

  A．{1，3，5}

  B．{1，2，5}

  C．{1，5}

  D．{2，5}
  組卷：4引用：1難度：0.7

  解析

• 5．下列函數中既是偶函數又在（0，+∞）上是增函數的是（　　）

  A．y= 1 x 2

  B．y=lgx

  C．y=x2+x

  D．y=2|x|
  組卷：1引用：1難度：0.7

  解析

• 6．要得到函數y=sin（2x+

  π

  2

  ）的圖象，只要將函數y=sin2x的圖象（　　）

  A．向右平移 π 2 個單位長度	B．向左平移 π 2 個單位長度
  C．向右平移 π 4 個單位長度	D．向左平移 π 4 個單位長度
  組卷：460引用：4難度：0.7

  解析

• 7．

  f

  （

  x

  ）

  =

  ln （ x 2 + a ） ， x ＜ 0

  f （ x - 2 ） ， x ≥ 0

  ，若f（2023）=1，則正數a的值是（　　）

  A．e+1

  B．e

  C．e-1

  D．1
  組卷：49引用：1難度：0.8

  解析
• 8．系統找不到該試題

二、不定項選擇題（本大題共4小題，共20.0分）

• 9．已知數列{a_n}滿足a₁=2，a_n+1=

  a n + 1 ， n 為奇數

  a n + 3 ， n 為偶數 ，

  ，記b_n=a_2n-1，則（　　）

  A．b1=3

  B．b2=6

  C．bn+1-bn=4

  D．bn=4n+2
  組卷：165引用：4難度：0.5

  解析

• 10．已知過點（0，1）的直線與橢圓x²+

  y

  2

  2

  =1交于A，B兩點，則弦長|AB|可能是（　　）

  A．1

  B． 2

  C． 3

  D．3
  組卷：101引用：7難度：0.5

  解析

• 11．假設α∈（0，π），且

  α

  ≠

  π

  2

  ．當∠xoy=α時，定義平面坐標系xOy為α-仿射坐標系，在α-仿射坐標系中，任意一點P的斜坐標這樣定義：

  e

  1

  ，

  e

  2

  分別為x軸，y軸正方向上的單位向量，若

  OP

  =

  x

  e

  1

  +

  y

  e

  2

  ，則記為

  OP

  =

  （

  x

  ,

  y

  ）

  ，那么下列說法中正確的是（　　）

  A．設 a = （ m , n ） ，則 | a | = m 2 + n 2 + 2 mncosα

  B．設 a = （ m , n ） ， b = （ s , t ） ，若 a ∥ b ，則mt-ns=0

  C．設 a = （ m , n ） ， b = （ s , t ） ，若 a ⊥ b ，則ms+nt+（mt+ns）sinα=0

  D．設 a = （ - 1 ， 2 ） ， b = （ - 2 ， 1 ） ，若 a 與 b 的夾角為 π 3 ，則 α = π 3
  組卷：90引用：4難度：0.5

  解析

• 12．已知實數x、y,令f（x,y）=λ[

  x

  2

  +

  y

  2

  +

  x

  2

  +

  （

  1

  -

  y

  ）

  2

  +

  （

  1

  -

  x

  ）

  2

  +

  y

  2

  +

  （

  1

  -

  x

  ）

  2

  +

  （

  1

  -

  y

  ）

  2

  ]

  +

  μ

  （

  1

  +

  x

  ）

  2

  +

  y

  2

  ?

  （

  1

  -

  x

  ）

  2

  +

  y

  2

  +μ

  （

  1

  +

  x

  ）

  2

  +

  y

  2

  ?

  （

  1

  -

  x

  ）

  2

  +

  y

  2

  ，下列說法中正確的是（　　）

  A．當λ=1，μ=0且0＜x＜1，0＜y＜1時，f（x,y）的最小值為 2 2

  B．當λ=1，μ=0且0＜x＜1，0＜y＜1，f（x,y）取最小值時，有序數對（x,y）的值有4個

  C．當λ=0，μ=1時，滿足 f （ x , y ） = 2 的點P（x,y）的軌跡關于O（0，0）對稱

  D．當λ=0，μ=1時，滿足f（x,y）=1的點P（x,y）到原點O（0，0）距離的最大值為 2
  組卷：84引用：3難度：0.3

  解析

三、填空題（本大題共4小題，共20.0分）

• 13．設

  1

  +

  i

  1

  -

  i

  =a+bi（i為虛數單位，a,b∈R），則ab的值為

   

  ．
  組卷：51引用：7難度：0.9

  解析

• 14．設

  m

  ，

  n

  是兩個單位向量，向量

  a

  =

  m

  -

  2

  n

  ，且

  |

  a

  |

  =

  5

  ，則

  m

  ?

  n

  =

  ．
  組卷：42引用：2難度：0.8

  解析

• 15．已知雙曲線C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0），直線x=a與C的兩條漸近線交于A，B兩點，O為坐標原點，若△OAB的面積為a²，則C的離心率為

  ．
  組卷：3引用：2難度：0.6

  解析

• 16．（1-ax²）（1+x）⁴的展開式中x³的系數為12，則a=

  ．
  組卷：170引用：5難度：0.8

  解析

四、解答題（本大題共6小題，共70分）

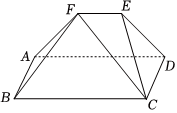• 17．如圖，幾何體ABCDEF中，ADEF為等腰梯形，ABCD為矩形，AD∥EF，AB=1，AD=3，DE=

  2

  ，EF=1，平面ADEF⊥平面ABCD．
  （1）證明：BF⊥CF；
  （2）求直線AF與平面CEF所成角的大小．
  組卷：39引用：1難度：0.5

  解析

• 18．已知數列{a_n}的前n項和為S_n，滿足：a₁=1，S_n+1-1=S_n+a_n，數列{b_n}為等比數列滿足b₁=4b₃，b₂=

  1

  4

  ＜b₁，n∈N*．
  （1）求數列{a_n}，{b_n}的通項公式；
  （2）若數列{

  1

  a

  n

  a

  n

  +

  1

  }的前n項和為W_n，數列{b_n}的前n項和為T_n，試比較W_n與T_n的大小．
  組卷：37引用：2難度：0.5

  解析

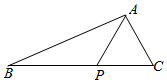• 19．如圖，在△ABC中，點P在BC邊上，∠PAC=60°，PC=2，AP+AC=4．
  （1）求∠ACP；
  （2）若△APB的面積是

  3

  2

  2

  ，求sin∠BAP．
  組卷：16引用：1難度：0.5

  解析

• 20．已知橢圓

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  經過A（0，2），B（-3，-1）兩點．
  （1）求橢圓上的動點T到N（1，0）的最短距離；
  （2）直線AB與x軸交于點M（m,0），過點M作不垂直于坐標軸且與AB不重合的直線l與橢圓交于C，D兩點，直線AC，BD分別交直線x=m于P，Q兩點．求證：

  |

  PM

  |

  |

  MQ

  |

  為定值．
  組卷：102引用：2難度：0.3

  解析

• 21．已知函數f（x）=x³-3ax²+3x+1
  （1）設a=2，求f（x）的單調增區間；
  （2）設f（x）在區間（2，3）中至少有一個極值點，求a的取值范圍．
  組卷：793引用：16難度：0.5

  解析

• 22．筆者隨機調查了福田區6個商店，其建筑面積x（千平方米）與年銷售額y（百萬元）數據如表所示：
  

  x（面積）	4	6	9	7	8	8
  y（銷售額）	3	5	6	4	5	7

  （1）求y關于x的回歸直線方程；
  （2）若線性關系存在，那么對于福田區一個擁有一萬平方米的商店來說，它的年銷售額約為多少？
  組卷：6引用：1難度：0.3

  解析