2023-2024學(xué)年江西省部分學(xué)校高三（上）月考數(shù)學(xué)試卷（12月份）

一、選擇題：本大題共8小題，每小題5分，共40分.在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的.

• 1．已知底面半徑為1的一個(gè)圓錐的展開(kāi)圖是一個(gè)圓心角等于120°的扇形，則該圓錐的體積為（　　）

  A． 2 π 3

  B． 2 2 π 3

  C． 2 3 π 3

  D． 2 π
  組卷：28引用：0難度：0.9

  解析

• 2．拋物線y²=x的準(zhǔn)線方程為（　　）

  A．x= 1 2

  B．x= 1 4

  C．x=- 1 2

  D．x=- 1 4
  組卷：275引用：5難度：0.8

  解析

• 3．在天文學(xué)中，天體的明暗程度可以用星等或亮度來(lái)描述．兩顆星的星等與亮度滿足

  m

  2

  -

  m

  1

  =

  5

  2

  lg

  E

  1

  E

  2

  ，其中星等為m_k的星的亮度為E_k（k=1，2）．已知太陽(yáng)的星等是-26.7，天狼星的星等是-1.45，則太陽(yáng)與天狼星的亮度的比值為（　　）

  A．1010.1

  B．10.1

  C．lg10.1

  D．10-10.1
  組卷：1534引用：22難度：0.7

  解析

• 4．若復(fù)數(shù)z滿足（1+3i）z=2+4i,則z的虛部為（　　）

  A． 1 5 i

  B． - 1 5 i

  C． - 1 5

  D． 7 5
  組卷：263引用：2難度：0.7

  解析

• 5．正四面體ABCD的棱長(zhǎng)為a,點(diǎn)E，F(xiàn)分別是BC，AD的中點(diǎn)，則

  AE

  ?

  AF

  的值為（　　）

  A．a(chǎn)2

  B． 1 2 a 2

  C． 1 4 a 2

  D． 3 4 a 2
  組卷：329引用：17難度：0.7

  解析

• 6．漢代數(shù)學(xué)家趙爽在注解《周髀算經(jīng)》時(shí)給出的“趙爽弦圖”是我國(guó)古代數(shù)學(xué)的瑰寶．如圖所示的弦圖由四個(gè)全等的直角三角形和一個(gè)正方形構(gòu)成．現(xiàn)用5種不同的顏色對(duì)這四個(gè)直角三角形和一個(gè)正方形區(qū)域涂色，要求相鄰的區(qū)域不能用同一種顏色，則不同的涂色方案有（　　）

  A．180

  B．192

  C．300

  D．420
  組卷：165引用：2難度：0.6

  解析

• 7．關(guān)于函數(shù)

  f

  （

  x

  ）

  =

  3

  sin

  2

  x

  -

  2

  co

  s

  2

  x

  +

  1

  有下述四個(gè)結(jié)論，其中結(jié)論錯(cuò)誤的是（　　）

  A． f （ π 3 ） = 2

  B．f（x）的圖象關(guān)于直線 x = π 3 對(duì)稱(chēng)

  C．f（x）的圖象關(guān)于 （ 7 24 π ， 0 ） 對(duì)稱(chēng)

  D．f（x）在 [ 0 ， π 3 ] 上單調(diào)遞增
  組卷：501引用：6難度：0.5

  解析
• 8．系統(tǒng)找不到該試題

二、選擇題：本大題共4小題，每小題5分，共20分.在每小題給出的選項(xiàng)中，有多項(xiàng)符合題目要求.全部選對(duì)的得5分，部分選對(duì)的得2分，有選錯(cuò)的得0分.

• 9．已知數(shù)列{a_n}的前n項(xiàng)和為S_n，下列說(shuō)法正確的是（　　）

  A．若Sn=2n2-6n+1，則an=4n-4

  B．若an=4n-25，則Sn的最小值為-66

  C．若an=4n-3，則數(shù)列{（-1）nan}的前17項(xiàng)和為-33

  D．若數(shù)列{an}為等差數(shù)列，且a1011+a1012＜0，a1000+a1024＞0，則當(dāng)Sn＜0時(shí)，n的最大值為2023
  組卷：549引用：8難度：0.5

  解析

• 10．正六棱臺(tái)的上、下底面邊長(zhǎng)分別是2cm和6cm,側(cè)棱長(zhǎng)是5cm,則下列說(shuō)法正確的是（　　）

  A．該正六棱臺(tái)的上底面積是 6 3 c m 2

  B．該正六棱臺(tái)的側(cè)面面積是15cm2

  C．該正六棱臺(tái)的表面積是 （ 60 3 + 24 21 ） c m 2

  D．該正六棱臺(tái)的高是3cm
  組卷：67引用：3難度：0.6

  解析

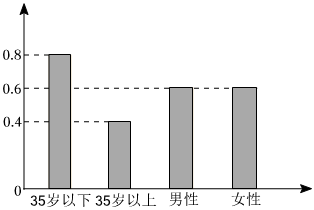• 11．手機(jī)支付已經(jīng)成為現(xiàn)如今最流行的支付方式，為了解年齡、性別與使用手機(jī)支付的關(guān)系，某市從本地居民中隨機(jī)抽取了容量為100的樣本，其中35歲以上和35歲以下的各50人，且男性60人，女性40人．根據(jù)以上數(shù)據(jù)，繪制了不同群體中使用手機(jī)支付與不使用手機(jī)支付的人數(shù)比例圖（如下圖所示），其中陰影部分表示使用手機(jī)支付的比例，則下列敘述中正確的有（　　）

  A．是否使用手機(jī)支付與年齡有關(guān)

  B．是否使用手機(jī)支付與性別無(wú)關(guān)

  C．使用手機(jī)支付的人員中，男性人數(shù)與女性人數(shù)相同

  D．不使用手機(jī)支付的人員中，35歲以上人數(shù)多于35歲以下的人數(shù)
  組卷：10引用：2難度：0.7

  解析

• 12．已知α∈[0，π]，則方程x²+y²cosα=1表示的曲線的形狀可以是（　　）

  A．兩條直線	B．圓
  C．焦點(diǎn)在x軸上的橢圓	D．焦點(diǎn)在x軸上的雙曲線
  組卷：44引用：6難度：0.7

  解析

三、填空題：本大題共4小題，每小題5分，共20分.把答案填在答題卡中的橫線上.

• 13．已知隨機(jī)變量X～B（6，0.8），若P（X=k）最大，則D（kX+1）=

  ．
  組卷：310引用：5難度：0.7

  解析

• 14．請(qǐng)寫(xiě)出一個(gè)同時(shí)滿足下列3個(gè)條件的函數(shù)f（x）（x∈R）：f（x）=

  ．
  ①f（-x）=f（x）；
  ②f（x）=f（x+1）；
  ③f（x）在

  [

  1

  2

  ，

  1

  ]

  上單調(diào)遞增．
  組卷：11引用：2難度：0.8

  解析

• 15．已知雙曲線

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的實(shí)軸為2

  6

  ，直線y=

  2

  3

  x與雙曲線交于A，B兩點(diǎn)，A，B兩點(diǎn)的橫坐標(biāo)之積為-9，則離心率e為

  ．
  組卷：1引用：0難度：0.6

  解析

• 16．定義[x]表示不超過(guò)x的最大整數(shù)，例如[2.1]=2，[-1.2]=-2．則方程x²-4[x]+3=0的解的個(gè)數(shù)為

  ．
  組卷：26引用：2難度：0.5

  解析

四、解答題：本大題共6小題，共70分.解答應(yīng)寫(xiě)出文字說(shuō)明、證明過(guò)程或演算步驟.

• 17．第33屆夏季奧林匹克運(yùn)動(dòng)會(huì)即將于2024年在巴黎舉辦，其中游泳比賽分為預(yù)賽、半決賽和決賽三個(gè)階段，只有預(yù)賽、半決賽都獲勝才有資格進(jìn)入決賽．已知甲在預(yù)賽和半決賽中獲勝的概率分別為

  1

  2

  和

  2

  3

  ，乙在預(yù)賽和半決賽中獲勝的概率分別為

  2

  3

  和

  3

  4

  ，丙在預(yù)賽和半決賽中獲勝的概率分別為p和

  4

  3

  -

  p

  ，其中

  1

  3

  ＜

  p

  ＜

  2

  3

  ．
  （1）甲、乙、丙三人中，哪個(gè)人進(jìn)入決賽的可能性更大？
  （2）如果甲、乙、丙三人中恰有兩人進(jìn)入決賽的概率為

  11

  36

  ，求p的值；
  （3）在（2）的條件下，設(shè)甲、乙、丙三人中進(jìn)入決賽的人數(shù)為ξ，求ξ的分布列．
  組卷：231引用：1難度：0.5

  解析

• 18．在四棱錐P-ABCD中，底面ABCD是邊長(zhǎng)為2的正方形，PC⊥PD，二面角A-CD-P為直二面角．
  （1）求證：PB⊥PD；
  （2）當(dāng)PC=PD時(shí)，求直線PC與平面PAB所成角的正弦值．
  組卷：1162引用：17難度：0.7

  解析

• 19．已知等比數(shù)列{a_n}中，a₂=32，

  a

  8

  =

  1

  2

  ，a_n+1＜a_n．
  （1）求數(shù)列{a_n}的通項(xiàng)公式；
  （2）設(shè)T_n=log₂a₁+log₂a₂+…+log₂a_n，求T_n的最大值及相應(yīng)的n值．
  組卷：81引用：10難度：0.3

  解析

• 20．在△ABC中，A，B，C的對(duì)邊分別為a,b,c,acosB-2acosC=（2c-b）cosA．
  （1）若c=

  3

  a,求cosB的值；
  （2）若b=1，∠BAC的平分線AD交BC于點(diǎn)D，求AD長(zhǎng)度的取值范圍．
  組卷：1786引用：14難度：0.6

  解析

• 21．設(shè)函數(shù)f（x）=x²+2x-2ln（1+x）．
  （Ⅰ）求函數(shù)f（x）的單調(diào)區(qū)間；
  （Ⅱ）當(dāng)

  x

  ∈

  [

  1

  e

  -

  1

  ，

  e

  -

  1

  ]

  時(shí)，是否存在整數(shù)m,使不等式m＜f（x）≤-m²+2m+e²恒成立？若存在，求整數(shù)m的值；若不存在，請(qǐng)說(shuō)明理由．
  （Ⅲ）關(guān)于x的方程f（x）=x²+x+a在[0，2]上恰有兩個(gè)相異實(shí)根，求實(shí)數(shù)a的取值范圍．
  組卷：121引用：7難度：0.5

  解析

• 22．已知拋物線C：y²=4x的準(zhǔn)線與x軸交于M點(diǎn)，過(guò)M點(diǎn)斜率為k的直線l與拋物線C交于A、B兩點(diǎn)（A在M、B之間）．
  （1）F為拋物線C的焦點(diǎn)，若|AM|=

  5

  4

  |AF|，求k的值；
  （2）如果拋物線C上總存在點(diǎn)Q，使得QA⊥QB，試求k的取值范圍．
  組卷：42引用：7難度：0.3

  解析