2024年貴州省普通高中學(xué)業(yè)水平合格性考試數(shù)學(xué)模擬試卷
發(fā)布：2025/11/13 12:0:35
一、選擇題：每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題意的。
-
1．一組數(shù)據(jù)為2，4，4，5，7，8，則這組數(shù)據(jù)的第60百分位數(shù)是（ ）
組卷：63引用：3難度：0.7 -
2．已知集合A={0，1，2，3，4}，B={2，3，4，5，6}，則A∩B=（ ）
組卷：70引用：6難度：0.8 -
3．在正方體ABCD-A1B1C1D1中，與棱AA1異面的棱有（ ）
組卷：569引用：9難度：0.8 -
4．已知某圓錐的內(nèi)切球（球與圓錐側(cè)面、底面均相切）的體積為
，則該圓錐的表面積的最小值為（ ）32π3組卷：445引用：6難度：0.5 -
5．從某網(wǎng)絡(luò)平臺(tái)推薦的影視作品中抽取400部，統(tǒng)計(jì)其評(píng)分?jǐn)?shù)據(jù)，將所得400個(gè)評(píng)分?jǐn)?shù)據(jù)分為8組：[66，70），[70，74），…，[94，98），并整理得到如下的頻率分布直方圖，則評(píng)分在區(qū)間[82，86）內(nèi)的影視作品數(shù)量是（ ）
組卷：2513引用：9難度：0.9 -
6．某人射擊一次命中目標(biāo)的概率為
，則此人射擊6次，3次命中且恰有2次連續(xù)命中的概率為（ ）12組卷：132引用：5難度：0.7 -
7．某市準(zhǔn)備建一所體育文化公園，針對(duì)公園中的體育設(shè)施，某社區(qū)采用分層隨機(jī)抽樣的方法對(duì)21歲至65歲的居民進(jìn)行了調(diào)查．已知該社區(qū)21歲至35歲的居民有840人，36歲至50歲的居民有700人，51歲至65歲的居民有560人．若從36歲至50歲的居民中隨機(jī)抽取了100人，則這次抽樣調(diào)查抽取的總?cè)藬?shù)是（ ）
組卷：78引用：6難度：0.9 -
8．函數(shù)y=x2-4x+3的零點(diǎn)為（ ）
組卷：472引用：5難度：0.7 -
9．不等式-x2-2x+8≤0的解集是（ ）
組卷：40引用：0難度：0.7 -
10．在△ABC中，三內(nèi)角A，B，C所對(duì)的邊分別為a,b,c,若b2+c2-a2=bc,sin2A+sin2B=sin2C，則B=（ ）
組卷：74引用：2難度：0.8 -
11．函數(shù)
的最小正周期為π，則f（x）=cos（ωx+π6）（ω＞0）=（ ）f（π2）組卷：3引用：4難度：0.7 -
12．已知函數(shù)
在（-∞，+∞）上單調(diào)遞減，則實(shí)數(shù)a的取值范圍是（ ）f（x）=（1-2a）x+1（x＜1）ax（x≥1）組卷：52引用：2難度：0.7 -
13．若函數(shù)f（x）=
-ax+1的圖象經(jīng)過四個(gè)象限，則實(shí)數(shù)a的取值范圍是（ ）13ax3組卷：97引用：3難度：0.4 -
14．已知向量
，a=（1，0），則b=（-12，32）=（ ）|a-b|組卷：230引用：2難度：0.8 -
15．函數(shù)
的定義域?yàn)椋ā 。?/h2>f（x）=2x-3+1x-3組卷：1372引用：17難度：0.8 -
16．如圖，角α以O(shè)x為始邊，它的終邊與單位圓O相交于點(diǎn)P，且點(diǎn)P的橫坐標(biāo)為，則35的值為（ ）sin（π2+α）組卷：913引用：9難度：0.7 -
17．已知函數(shù)f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的極大值與極小值之差為2，且
對(duì)?x∈R恒成立，f（x）≤f（π6），f（x）在f（2π3）=0上單調(diào)遞減，若將函數(shù)f（x）的圖象向左平移（π6，2π3）個(gè)單位長度得到函數(shù)g（x）的圖象，則下列結(jié)論錯(cuò)誤的是（ ）π6組卷：120引用：3難度：0.5 -
18．若實(shí)數(shù)a,b滿足a＜b＜0，則下列不等式正確的是（ ）
組卷：330引用：8難度：0.8 -
19．給出下列命題：
①曲線的切線一定和曲線只有一個(gè)交點(diǎn)；
②“可導(dǎo)函數(shù)y=f（x）在一點(diǎn)的導(dǎo)數(shù)值為0”是“函數(shù)y=f（x）在這點(diǎn)取得極值”的必要不充分條件；
③若f（x）在（a,b）內(nèi)存在導(dǎo)數(shù)，則“f′（x）＜0”是f（x）在（a,b）內(nèi)單調(diào)遞減的充要條件；
④求曲邊梯形的面積用到了“以直代曲”的思想，在“近似代替”中，函數(shù)f（x）在區(qū)間[xi，xi+1]上的近似值可以是該區(qū)間內(nèi)任一點(diǎn)的函數(shù)值f（ξi）（ξi∈[xi，xi+1]）
其中正確的個(gè)數(shù)是（ ）組卷：8引用：1難度：0.5 -
20．若復(fù)數(shù)z=2-3i,則該復(fù)數(shù)的實(shí)部和虛部分別為（ ）
組卷：87引用：6難度：0.9 -
21．系統(tǒng)找不到該試題
-
22．系統(tǒng)找不到該試題
二、填空題：本題共5小題，每小題3分，共15分。
-
23．計(jì)算：（2+
1027+2log32-log3）-23-49=．5log259組卷：191引用：4難度：0.8 -
24．已知事件A的對(duì)立事件為
，若P（A）=0.5，則P（A）=．A組卷：760引用：1難度：0.7 -
25．方程
的解集為．lg（x+1）4=（log214）2組卷：17引用：2難度：0.7 -
26．方程
的解集為lg（x+1）4=（log214）2．組卷：2引用：1難度：0.9 -
27．已知α為第四象限角，
，則sinα-cosα=．sinα+cosα=13組卷：57引用：2難度：0.7
三、解答題：本題共3小題，共19分.解答應(yīng)寫出文字說明、證明過程或推演步驟。
-
28．已知函數(shù)
是定義在（-2，2）上的奇函數(shù)，且f（x）=ax+bx2+4．f（12）=217
（1）求a,b的值；
（2）用單調(diào)性定義證明：函數(shù)f（x）在區(qū)間（-2，2）上單調(diào)遞增；
（3）若f（a+1）+f（1-2a）＞0，求實(shí)數(shù)a的取值范圍．組卷：142引用：6難度：0.5 -
29．寫出下列命題的否定．
（1）有些四邊形的四個(gè)頂點(diǎn)在同一個(gè)圓上；
（2）?x∈Q，；12x2-13x+1∈Q
（3）所有能被3整除的數(shù)都是奇數(shù)；
（4）?a＜1，；a+1a=2
（5）不論m取何實(shí)數(shù)，方程x2+x-m=0必有實(shí)數(shù)根．組卷：45引用：1難度：0.8 -
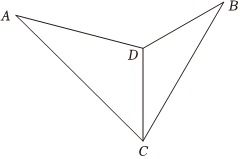30．某景區(qū)有一人工湖，湖面有A，B兩點(diǎn)，湖邊架有直線型棧道CD，長為50m,如圖所示．現(xiàn)要測(cè)量A，B兩點(diǎn)之間的距離，工作人員分別在C，D兩點(diǎn)進(jìn)行測(cè)量，在C點(diǎn)測(cè)得∠ACD=45°，∠BCD=30°；在D點(diǎn)測(cè)得∠ADB=135°，∠BDC=120°．（A，B，C，D在同一平面內(nèi)）
（Ⅰ）求A，B兩點(diǎn)之間的距離；
（Ⅱ）判斷直線CD與直線AB是否垂直，并說明理由．組卷：234引用：8難度：0.5