當前位置：試卷中心 > 試卷詳情

2021年山東省臨沂市沂水一中高考數學二輪模擬檢測試卷（4月份）

發布：2025/11/13 13:0:26

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的.

1．△ABC中∠C=90°，AC=2，P為線段BC上任一點，則
AP
?
AC
=（　　）
A．2 B．4 C．8 D．不確定
組卷：111引用：3難度：0.8
2．若橢圓
x
2
25
+
y
2
16
=
1
上一點P到橢圓一個焦點的距離為4，則P到另一個焦點的距離為（　　）
A．3 B．4 C．5 D．6
組卷：35引用：2難度：0.7
3．已知集合A={x|x-1＞0}，B={x|x²-2x≤0}，則A∩B=（　　）
A．[0，2] B．[1，2） C．（1，2] D．[2，+∞）
組卷：248引用：7難度：0.8
4．已知函數f（x）的定義域是 R，函數f（x+1）的圖象的對稱中心是（-1，0），若對任意的x₁，x₂∈（0，+∞），且x₁≠x₂，都有
x
2
f
（
x
1
）
-
x
1
f
（
x
2
）
x
1
-
x
2
＞
0
成立，f（1）=1，則不等式f（x）-x＞0的解集為（　　）
A．（-∞，-1）∪（1，+∞） B．（-1，1）
C．（-∞，-1）∪（0，1） D．（-1，0）∪（1，+∞）
組卷：352引用：12難度：0.5
5．復數z=（1-i）i的虛部是（　　）
A．i B．-i C．-1 D．1
組卷：103引用：8難度：0.9
6．從2，4中選一個數字，從1，3，5中選兩個數字，組成無重復數字的三位奇數的個數為（　　）
A．12 B．18 C．24 D．36
組卷：49引用：1難度：0.7
7．已知球O的一個截面的面積為2π，球心O到該截面的距離比球的半徑小1，則球O的表面積為（　　）
A．8π B．9π C．12π D．16π
組卷：71引用：2難度：0.7
8．雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，過F₁的直線與雙曲線C的右支在第一象限的交點為A，與y軸的交點為B，且B為AF₁的中點，若△ABF₂的周長為6a,則雙曲線C的漸近線方程為（　　）
A．
y
=±
3
x
B．
y
=±
2
x
C．
y
=±
3
2
x
D．
y
=±
2
2
x
組卷：699引用：6難度：0.5

二.多項選擇題：本題共4小題，每小題5分，共20分.在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，部分選對的得3分，有選錯的得0分.

9．2022年9月錢塘江多處出現罕見潮景“魚鱗潮”，“魚鱗潮”的形成需要兩股涌潮，一股是波狀涌潮，另外一股是破碎的涌潮，兩者相遇交叉就會形成像魚鱗一樣的涌潮．若波狀涌潮的圖像近似函數
f
（
x
）
=
A
sin
（
ωx
+
φ
）
（
A
，
ω
∈
N
*
，
|
φ
|
＜
π
3
）
的圖像，而破碎的涌潮的圖像近似f'（x）（f'（x）是函數f（x）的導函數）的圖像．已知當x=2π時，兩潮有一個交叉點，且破碎的涌潮的波谷為-4，則（　　）
A．ω=2
B．
f
（
π
3
）
=
6
+
2
C．
f
′
（
x
-
π
4
）
是偶函數
D．f'（x）在區間
（
-
π
3
，
0
）
上單調
組卷：203引用：11難度：0.6
10．在四面體ABCD中，有四條棱的長度為1，兩條棱的長度為m,則（　　）
A．當AB=AD=m時，AC⊥BD
B．當AB=CD=m時，四面體ABCD的外接球的表面積為
（
m
2
+
2
）
π
2
C．m的取值范圍為
（
0
，
2
）
D．四面體ABCD體積的最大值為
3
12
組卷：120引用：1難度：0.3

11．下列說法正確的是（　　）

A．若奇函數f（x）=x³+（b-1）x²+sinx的定義域為[a-1，2a+1]，則a+b=1

B．冪函數圖像一定不過第四象限

C．

sin

（

）

最小正周期為π

D．若lna＜1，則a的取值范圍是（-∞，e）

組卷：3引用：1難度：0.6

12．已知（log₂a+log₃a）-（log₂b+log₃b）＜log₃6，且a＞b＞0，則下列不等式成立的有（　　）
A．a＞2b B．
1
a
-
b
＞
1
b
C．
4
a
+
1
2
b
＞
4
D．
4
b
+
1
2
a
＞
2
組卷：81引用：3難度：0.5

三、填空題：本大題共4小題，每小題5分，

13．設S_n為數列{a_n}的前n項和，已知a₁=2，對任意p、q∈N^*，都有a_p+q=a_p+a_q，則f（n）=
S
n
+
60
n
+
1
（n∈N^*）的最小值為
．
組卷：431引用：15難度：0.5
14．現有10個數，它們能構成一個以l為首項，-3為公比的等比數列，若從這10個數中隨機抽取一個數，則這個數大于8的概率是

．
組卷：10引用：2難度：0.7
15．拋物線有如下光學性質：過焦點的光線經拋物線反射后得到的光線平行于拋物線的對稱軸；反之，平行于拋物線對稱軸的入射光線經拋物線反射后得到的光線必過拋物線的焦點．已知拋物線y²=16x的焦點為F，一條平行于x軸的光線從點M（4，4）射出，經過拋物線上的點A反射后，到達拋物線上的點B，則|AB|=
．
組卷：103引用：3難度：0.5
16．下列說法正確的序號為
．
①cos15°cos105°-sin15°sin105°=-
1
2
；
②已知cosα+cosβ=
3
5
，sinα+sinβ=
4
5
，則cos（α-β）=
-
26
25
；
③cos75°cos15°+sin75°sin15°=
1
2
．
組卷：5引用：1難度：0.7

四、解答題：本大題共6個大題，共70分，解答應寫出文字說明、證明過程或演算步驟.

17．已知函數f（x）=lnx-ax-1（a＞0）．
（1）當a=0時，求過原點且與f（x）的圖象相切的直線方程；
（2）若
g
（
x
）
=
e
-
ax
+
f
（
x
）
x
（
a
＞
0
）
有兩個不同的零點x₁、x₂（0＜x₁＜x₂），不等式
x
1
?
x
3
2
＞
e
m
恒成立，求實數m的取值范圍．
組卷：84引用：6難度：0.5
18．在△ABC中，a=3，
b
=
7
，c=2，求∠B，S_△ABC．
組卷：4引用：1難度：0.7
19．已知S_n是等差數列{a_n}的前n項和，a_n＞0，S₃=15，公差d＞1，且 _____．從①a₂-1為a₁-1與a₃+1等比中項，②等比數列{b_n}的公比為
q
=
1
2
，b₁=a₂，b₃=a₃這兩個條件中，選擇一個補充在上面問題的橫線上，使得符合條件的數列{a_n}存在并作答．
（1）求數列{a_n}的通項公式；
（2）設數列
{
1
a
n
a
n
+
1
}
的前n項和為T_n，求證：
T
n
＜
1
6
．
注：如果選擇多個條件分別解答，按第一個解答計分．
組卷：35引用：1難度：0.5
20．已知橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
過點
（
1
，
3
2
）
，且焦距為
2
3
．
（1）求橢圓C的標準方程；
（2）若Q為x軸上一定點（m,0），過點Q的直線與橢圓交于A，B兩點，點B關于x軸的對稱點為B′（B′，A，B三點互異），直線AB′交x軸于點P，試探究|OP|?|OQ|是否為定值，若為定值，并求出該定值．
組卷：18引用：2難度：0.5

21．期末考試結束后，隨機抽查了某校高三（1）班5名同學的數學與物理成績，如下表：

學生 1 2 3 4 5

數學 89 91 93 95 97

物理 87 89 89 92 93

（1）分別求這5名同學數學與物理成績的平均分與方差，并估計該班數學與物理成績那科更穩定．
（2）從4名數學成績在90分以上的同學中選2人參加一項活動，以X表示選中同學的物理成績高于90分的人數，求隨機變量X的分布列及數學期望E（X）的值．

組卷：8引用：3難度：0.5

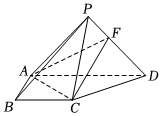22．如圖，在四棱錐P-ABCD中，側面PAD⊥底面ABCD，側棱
PA
=
PD
=
2
，底面ABCD為直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，
PF
=
1
2
FD
．
（1）求證：PB∥平面ACF；
（2）在線段PB上是否存在一點H，使得CH與平面ACF所成角的余弦值為
30
6
？若存在，求出線段PH的長度；若不存在，請說明理由．
組卷：215引用：6難度：0.5

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2021年山東省臨沂市沂水一中高考數學二輪模擬檢測試卷（4月份）

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的.

1．△ABC中∠C=90°，AC=2，P為線段BC上任一點，則
AP
?
AC
=（　　）

2．若橢圓
x
2
25
+
y
2
16
=
1
上一點P到橢圓一個焦點的距離為4，則P到另一個焦點的距離為（　　）

3．已知集合A={x|x-1＞0}，B={x|x²-2x≤0}，則A∩B=（　　）

4．已知函數f（x）的定義域是 R，函數f（x+1）的圖象的對稱中心是（-1，0），若對任意的x₁，x₂∈（0，+∞），且x₁≠x₂，都有
x
2
f
（
x
1
）
-
x
1
f
（
x
2
）
x
1
-
x
2
＞
0
成立，f（1）=1，則不等式f（x）-x＞0的解集為（　　）

5．復數z=（1-i）i的虛部是（　　）

6．從2，4中選一個數字，從1，3，5中選兩個數字，組成無重復數字的三位奇數的個數為（　　）

7．已知球O的一個截面的面積為2π，球心O到該截面的距離比球的半徑小1，則球O的表面積為（　　）

8．雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，過F₁的直線與雙曲線C的右支在第一象限的交點為A，與y軸的交點為B，且B為AF₁的中點，若△ABF₂的周長為6a,則雙曲線C的漸近線方程為（　　）

二.多項選擇題：本題共4小題，每小題5分，共20分.在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，部分選對的得3分，有選錯的得0分.

10．在四面體ABCD中，有四條棱的長度為1，兩條棱的長度為m,則（　　）

11．下列說法正確的是（　　）

12．已知（log₂a+log₃a）-（log₂b+log₃b）＜log₃6，且a＞b＞0，則下列不等式成立的有（　　）

三、填空題：本大題共4小題，每小題5分，

13．設S_n為數列{a_n}的前n項和，已知a₁=2，對任意p、q∈N^，都有a_p+q=a_p+a_q，則f（n）=
S
n
+
60
n
+
1
（n∈N^）的最小值為
．

14．現有10個數，它們能構成一個以l為首項，-3為公比的等比數列，若從這10個數中隨機抽取一個數，則這個數大于8的概率是

．

16．下列說法正確的序號為
．
①cos15°cos105°-sin15°sin105°=-
1
2
；
②已知cosα+cosβ=
3
5
，sinα+sinβ=
4
5
，則cos（α-β）=
-
26
25
；
③cos75°cos15°+sin75°sin15°=
1
2
．

四、解答題：本大題共6個大題，共70分，解答應寫出文字說明、證明過程或演算步驟.

18．在△ABC中，a=3，
b
=
7
，c=2，求∠B，S_△ABC．

A．（-∞，-1）∪（1，+∞）	B．（-1，1）
C．（-∞，-1）∪（0，1）	D．（-1，0）∪（1，+∞）

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2021年山東省臨沂市沂水一中高考數學二輪模擬檢測試卷（4月份）

一、單項選擇題：本題共8小題，每小題5分，共40分．在每小題給出的四個選項中，只有一項是符合題目要求的.

1．△ABC中∠C=90°，AC=2，P為線段BC上任一點，則AP?AC=（ ）

2．若橢圓x225+y216=1上一點P到橢圓一個焦點的距離為4，則P到另一個焦點的距離為（ ）

3．已知集合A={x|x-1＞0}，B={x|x2-2x≤0}，則A∩B=（ ）

4．已知函數f（x）的定義域是 R，函數f（x+1）的圖象的對稱中心是（-1，0），若對任意的x1，x2∈（0，+∞），且x1≠x2，都有x2f（x1）-x1f（x2）x1-x2＞0成立，f（1）=1，則不等式f（x）-x＞0的解集為（ ）

5．復數z=（1-i）i的虛部是（ ）

6．從2，4中選一個數字，從1，3，5中選兩個數字，組成無重復數字的三位奇數的個數為（ ）

7．已知球O的一個截面的面積為2π，球心O到該截面的距離比球的半徑小1，則球O的表面積為（ ）

8．雙曲線C：x2a2-y2b2=1（a＞0，b＞0）的左、右焦點分別為F1，F2，過F1的直線與雙曲線C的右支在第一象限的交點為A，與y軸的交點為B，且B為AF1的中點，若△ABF2的周長為6a,則雙曲線C的漸近線方程為（ ）

二.多項選擇題：本題共4小題，每小題5分，共20分.在每小題給出的選項中，有多項符合題目要求。全部選對的得5分，部分選對的得3分，有選錯的得0分.

10．在四面體ABCD中，有四條棱的長度為1，兩條棱的長度為m,則（ ）

11．下列說法正確的是（ ）

12．已知（log2a+log3a）-（log2b+log3b）＜log36，且a＞b＞0，則下列不等式成立的有（ ）

三、填空題：本大題共4小題，每小題5分，

13．設Sn為數列{an}的前n項和，已知a1=2，對任意p、q∈N*，都有ap+q=ap+aq，則f（n）=Sn+60n+1（n∈N*）的最小值為．

14．現有10個數，它們能構成一個以l為首項，-3為公比的等比數列，若從這10個數中隨機抽取一個數，則這個數大于8的概率是 ．

16．下列說法正確的序號為 ．①cos15°cos105°-sin15°sin105°=-12；②已知cosα+cosβ=35，sinα+sinβ=45，則cos（α-β）=-2625；③cos75°cos15°+sin75°sin15°=12．

四、解答題：本大題共6個大題，共70分，解答應寫出文字說明、證明過程或演算步驟.

17．已知函數f（x）=lnx-ax-1（a＞0）．（1）當a=0時，求過原點且與f（x）的圖象相切的直線方程；（2）若g（x）=e-ax+f（x）x（a＞0）有兩個不同的零點x1、x2（0＜x1＜x2），不等式x1?x32＞em恒成立，求實數m的取值范圍．

18．在△ABC中，a=3，b=7，c=2，求∠B，S△ABC．

1．△ABC中∠C=90°，AC=2，P為線段BC上任一點，則
AP
?
AC
=（　　）

2．若橢圓
x
2
25
+
y
2
16
=
1
上一點P到橢圓一個焦點的距離為4，則P到另一個焦點的距離為（　　）

3．已知集合A={x|x-1＞0}，B={x|x²-2x≤0}，則A∩B=（　　）

4．已知函數f（x）的定義域是 R，函數f（x+1）的圖象的對稱中心是（-1，0），若對任意的x₁，x₂∈（0，+∞），且x₁≠x₂，都有
x
2
f
（
x
1
）
-
x
1
f
（
x
2
）
x
1
-
x
2
＞
0
成立，f（1）=1，則不等式f（x）-x＞0的解集為（　　）

5．復數z=（1-i）i的虛部是（　　）

6．從2，4中選一個數字，從1，3，5中選兩個數字，組成無重復數字的三位奇數的個數為（　　）

7．已知球O的一個截面的面積為2π，球心O到該截面的距離比球的半徑小1，則球O的表面積為（　　）

8．雙曲線C：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的左、右焦點分別為F₁，F₂，過F₁的直線與雙曲線C的右支在第一象限的交點為A，與y軸的交點為B，且B為AF₁的中點，若△ABF₂的周長為6a,則雙曲線C的漸近線方程為（　　）

10．在四面體ABCD中，有四條棱的長度為1，兩條棱的長度為m,則（　　）

11．下列說法正確的是（　　）

12．已知（log₂a+log₃a）-（log₂b+log₃b）＜log₃6，且a＞b＞0，則下列不等式成立的有（　　）

13．設S_n為數列{a_n}的前n項和，已知a₁=2，對任意p、q∈N^，都有a_p+q=a_p+a_q，則f（n）=
S
n
+
60
n
+
1
（n∈N^）的最小值為
．

14．現有10個數，它們能構成一個以l為首項，-3為公比的等比數列，若從這10個數中隨機抽取一個數，則這個數大于8的概率是

．

16．下列說法正確的序號為
．
①cos15°cos105°-sin15°sin105°=-
1
2
；
②已知cosα+cosβ=
3
5
，sinα+sinβ=
4
5
，則cos（α-β）=
-
26
25
；
③cos75°cos15°+sin75°sin15°=
1
2
．

18．在△ABC中，a=3，
b
=
7
，c=2，求∠B，S_△ABC．