當(dāng)前位置：試卷中心 > 試卷詳情

2019-2020學(xué)年湖北省十堰市高三（上）期末數(shù)學(xué)試卷（文科）（元月調(diào)考）

發(fā)布：2025/11/13 13:0:26

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

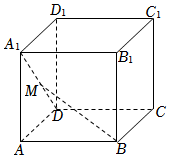1．如圖，正方體ABCD-A₁B₁C₁D₁中，M是A₁D的中點(diǎn)，則（　　）

A．直線MB與直線B₁D₁相交，直線MB?平面ABC₁

B．.直線MB與直線D₁C平行，直線MB⊥平面A₁C₁D

C．直線MB與直線AC異面，直線MB⊥平面ADC₁B₁

D．直線MB與直線A₁D垂直，直線MB∥平面B₁D₁C

組卷：1034引用：10難度：0.5

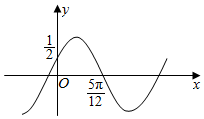2．已知曲線C₁：y=sinx,曲線C₂：
y
=
sin
（
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分圖像如圖所示，則下列結(jié)論正確的是（　　）

A．將曲線C₁先向左平移

個(gè)單位長(zhǎng)度，再將各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來的2倍，得到曲線C₂

B．將曲線C₁先向左平移

個(gè)單位長(zhǎng)度，再將各點(diǎn)的橫坐標(biāo)縮短到原來的

倍，得到曲線C₂

C．將曲線C₁先向左平移

個(gè)單位長(zhǎng)度，再將各點(diǎn)的橫坐標(biāo)伸長(zhǎng)到原來的2倍，得到曲線C₂

D．將曲線C₁先向左平移

個(gè)單位長(zhǎng)度，再將各點(diǎn)的橫坐標(biāo)縮短到原來的

倍，得到曲線C₂

組卷：273引用：2難度：0.6

3．若復(fù)數(shù)z滿足（1+3i）z=2+4i,則z的虛部為（　　）
A．
1
5
i
B．
-
1
5
i
C．
-
1
5
D．
7
5
組卷：263引用：2難度：0.7
4．在正三棱柱ABC-A'B'C'中，D是側(cè)棱BB'上一點(diǎn)，E是側(cè)棱CC'上一點(diǎn)，若線段AD+DE+EA'的最小值是
2
7
，且其內(nèi)部存在一個(gè)內(nèi)切球（與該棱柱的所有面均相切），則該棱柱的外接球表面積為（　　）
A．4π B．5π C．6π D．8π
組卷：50引用：3難度：0.5
5．已知等軸雙曲線的焦距為8，左、右焦點(diǎn)F₁，F(xiàn)₂在x軸上，中心在原點(diǎn)，點(diǎn)A的坐標(biāo)為
（
2
，
2
3
）
，P為雙曲線右支上一動(dòng)點(diǎn)，則|PF₁|+|PA|的最小值為（　　）
A．
2
2
+
2
B．
2
2
+
4
C．
4
2
+
2
D．
4
2
+
4
組卷：142引用：4難度：0.6
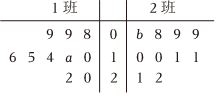6．某校初一（1）班和初一（2）班各有10人騎自行車上學(xué)，他們每天騎行路程（單位：千米）的莖葉圖如圖所示，則1班10人每天騎行路程的極差和2班10人每天騎行路程的中位數(shù)分別是（　　）
A．14，9.5 B．9，9 C．9，10 D．14，10
組卷：53引用：1難度：0.7
7．拋物線C：y²=-12x的焦點(diǎn)為F，P為拋物線C上一動(dòng)點(diǎn)，定點(diǎn)A（-5，2），則|PA|+|PF|的最小值為（　　）
A．8 B．6 C．5 D．9
組卷：559引用：7難度：0.6
8．已知函數(shù)f（x）=
2
x
1
+
2
x
，則對(duì)任意實(shí)數(shù)x,有（　　）
A．f（-x）+f（x）=1 B．f（-x）-f（x）=0
C．f（-x）+f（x）=0 D．f（-x）-f（x）=-1
組卷：297引用：4難度：0.8
9．已知函數(shù)f（x）的定義域?yàn)锽，函數(shù)f（1-2x）的定義域?yàn)?div id="gakugmc" class="MathJye" mathtag="math">
A
=
[
-
1
2
，
1
2
）
，若?x∈B，使得x²-mx+2＞0恒成立，則實(shí)數(shù)m的取值范圍為（　　）

A．（-∞，3）

B．（3，+∞）

C．

（

∞

，

）

D．

（

，

∞

）

組卷：97引用：7難度：0.5

10．已知集合A={x|x-1＞0}，B={x|x²-2x≤0}，則A∩B=（　　）

A．[0，2]

B．[1，2）

C．（1，2]

D．[2，+∞）

組卷：248引用：7難度：0.8

11．已知等比數(shù)列的前n項(xiàng)和S_n=4ⁿ+a,則a的值等于（　　）

A．-4

B．-1

C．0

D．1

組卷：398引用：10難度：0.9

12．執(zhí)行如圖所示的程序框圖，輸出的結(jié)果為（　　）

A．64

B．32

C．16

D．5

組卷：71引用：3難度：0.9

二、填空題：本大題共4小題，每小題5分，共20分．

13．若S_n數(shù)列{a_n}的前n項(xiàng)和，且對(duì)任意的正整數(shù)n,有S_n=2a_n-1，則a₁=
，S_n=
．
組卷：2引用：2難度：0.6

14．如圖為一個(gè)開關(guān)陣列，每個(gè)開關(guān)只有“開”和“關(guān)”兩種狀態(tài)，按其中一個(gè)開關(guān)1次，將導(dǎo)致自身和所有相鄰（上、下相鄰或左、右相鄰）的開關(guān)改變狀態(tài)．若從這十六個(gè)開關(guān)中隨機(jī)選兩個(gè)不同的開關(guān)先后各按1次（例如：先按（1，1），再按（4，4）），則（2，3）和（4，1）的最終狀態(tài)都未發(fā)生改變的概率為
．

（1，1）（1，2）（1，3）（1，4）

（2，1）（2，2）（2，3）（2，4）

（3，1）（3，2）（3，3）（3，4）

（4，1）（4，2）（4，3）（4，4）

組卷：89引用：9難度：0.6

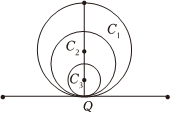15．在平面曲線中，曲率（curvature）是表示曲線在某一點(diǎn)的彎曲程度的數(shù)值，如圖，圓C₁、C₂、C₃在點(diǎn)Q處的彎曲程度依次增大，而直線在點(diǎn)Q處的彎曲程度最小，曲率越大，表示曲線的彎曲程度越大．曲線的曲率定義如下：若f′（x）是f（x）的導(dǎo)函數(shù)，f″（x）是f'（x）的導(dǎo)函數(shù)，則曲線y=f（x）在點(diǎn)（x,f（x））處的曲率K=
|
f
″
（
x
）
|
{
1
+
[
f
′
（
x
）
]
2
}
3
2
，則余弦曲線f（x）=cosx在（0，1）處的曲率為
．
組卷：22引用：1難度：0.7
16．已知向量
a
，
b
滿足
|
a
|
=
5
，
|
b
|
=
2
，且
a
在
b
上的投影向量為
2
b
，則
a
，
b
夾角的余弦值為
，
a
?
b
=
．
組卷：101引用：4難度：0.7

三、解答題：共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟，第17～21題為必考題，每道試題考生都必須作答．第22、23題為選考題，考生根據(jù)要求作答．（一）必考題：共60分．

17．設(shè)函數(shù)f（x）=5-|x+a|-|x-2|．
（1）當(dāng)a=1時(shí)，求不等式f（x）≥0的解集；
（2）若f（x）≤1，求a的取值范圍．
組卷：4435引用：35難度：0.5
18．以直角坐標(biāo)系的原點(diǎn)O為極點(diǎn)，x軸的正半軸為極軸，建立極坐標(biāo)系，且在兩種坐標(biāo)系中取相同的長(zhǎng)度單位．曲線C的極坐標(biāo)方程是ρ²=
16
1
+
3
co
s
2
θ
．
（Ⅰ）求曲線C的直角坐標(biāo)方程；
（Ⅱ）設(shè)曲線C與x軸正半軸及y軸正半軸交于點(diǎn)M，N，在第一象限內(nèi)曲線C上任取一點(diǎn)P，求四邊形OMPN面積的最大值．
組卷：155引用：4難度：0.5
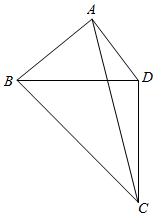19．為了美化環(huán)境，某公園欲將一塊空地規(guī)劃建成休閑草坪，休閑草坪的形狀為如圖所示的四邊形ABCD．其中AB=3百米，AD=
5
百米，且△BCD是以D為直角頂點(diǎn)的等腰直角三角形．?dāng)M修建兩條小路AC，BD（路的寬度忽略不計(jì)），設(shè)∠BAD=θ，θ∈（
π
2
，π）．
（1）當(dāng)cosθ=
-
5
5
時(shí)，求小路AC的長(zhǎng)度；
（2）當(dāng)草坪ABCD的面積最大時(shí)，求此時(shí)小路BD的長(zhǎng)度．
組卷：762引用：20難度：0.4

20．電子郵件是一種用電子手段提供信息交換的通信方式，是互聯(lián)網(wǎng)應(yīng)用最廣的服務(wù)．我們?cè)谑褂秒娮余]件時(shí)發(fā)現(xiàn)一個(gè)有趣的現(xiàn)象：中國(guó)人的郵箱名稱里含有數(shù)字的比較多，而外國(guó)人郵箱名稱里含有數(shù)字的比較少．為了研究郵箱名稱里含有數(shù)字是否與國(guó)籍有關(guān)，隨機(jī)調(diào)取了40個(gè)郵箱名稱，得到如下2×2列聯(lián)表：

中國(guó)人外國(guó)人總計(jì)

郵箱名稱里有數(shù)字 15 5 20

郵箱名稱里無數(shù)字 5 15 20

總計(jì) 20 20 40

（1）根據(jù)小概率值α=0.001的獨(dú)立性檢驗(yàn)，分析“郵箱名稱里含有數(shù)字與國(guó)籍”是否有關(guān)？
（2）用樣本估計(jì)總體，將頻率視為概率．在中國(guó)人郵箱名稱里和外國(guó)人郵箱名稱里各隨機(jī)抽取6個(gè)郵箱名稱，記“6個(gè)中國(guó)人郵箱名稱里恰有3個(gè)含有數(shù)字”的概率為P₁，“6個(gè)外國(guó)人郵箱名稱里恰有3個(gè)含有數(shù)字”的概率為P₂，試比較P₁與P₂的大小．
參考公式和數(shù)據(jù)：Χ²=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
，n=a+b+c+d.

α 0.10 0.05 0.025 0.010 0.005 0.001

Χ_α 2.706 3.841 5.024 6.635 7.879 10.828

組卷：105引用：2難度：0.5

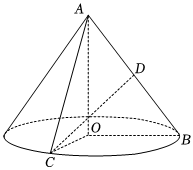21．如圖，在Rt△AOB中，∠OAB=
π
6
，斜邊AB=4，D是AB的中點(diǎn)，現(xiàn)將Rt△AOB以直角邊AO為軸旋轉(zhuǎn)一周得到一個(gè)圓錐，點(diǎn)C為圓錐底面圓周上的一點(diǎn)，且∠BOC=90°．
（1）求圓錐的表面積；
（2）若某動(dòng)點(diǎn)在圓錐側(cè)面上運(yùn)動(dòng)，試求該動(dòng)點(diǎn)從點(diǎn)C出發(fā)運(yùn)動(dòng)到點(diǎn)D所經(jīng)過的最短距離；
（3）若一個(gè)棱長(zhǎng)為a的正方體木塊可以在這個(gè)圓錐內(nèi)任意轉(zhuǎn)動(dòng)，求a的最大值．
組卷：123引用：2難度：0.5

四、選考題：共10分，請(qǐng)考生在第22、23題中任選一題作答，如果多做，則按所做的第一題計(jì)分．

22．設(shè)函數(shù)
f
（
x
）
=
lnx
x
，函數(shù)
g
（
x
）
=
2
e
x
-
（
a
+
b
）
x
-
f
（
1
a
）
-
f
（
1
b
）
-
（
a
+
b
）
，其中0＜a＜b,（e是自然對(duì)數(shù)的底數(shù)）．
（1）求函數(shù)f（x）在x=e處的切線方程；
（2）記函數(shù)g（x）的最小值為φ（a,b）．求證：φ（a,b）＜（b-a）ln2．
組卷：25引用：1難度：0.6
23．已知橢圓C：
x
2
a
2
+
y
2
b
2
=1（a＞b＞0）經(jīng)過點(diǎn)M（1，
2
2
），N（
2
，0）．
（1）求橢圓C的方程；
（2）已知直線l的傾斜角為銳角，l與圓x²+y²=
1
2
相切，與橢圓C交于A、B兩點(diǎn)，且△AOB的面積為
2
3
，求直線l的方程．
組卷：265引用：3難度：0.6

0/60 進(jìn)入組卷

0/20 進(jìn)入試卷籃

布置作業(yè) 發(fā)布測(cè)評(píng) 反向細(xì)目表 平行組卷 下載答題卡 試卷分析 在線訓(xùn)練 收藏試卷

充值會(huì)員，資源免費(fèi)下載

A．f（-x）+f（x）=1	B．f（-x）-f（x）=0
C．f（-x）+f（x）=0	D．f（-x）-f（x）=-1

（1，1）	（1，2）	（1，3）	（1，4）
（2，1）	（2，2）	（2，3）	（2，4）
（3，1）	（3，2）	（3，3）	（3，4）
（4，1）	（4，2）	（4，3）	（4，4）

	中國(guó)人	外國(guó)人	總計(jì)
郵箱名稱里有數(shù)字	15	5	20
郵箱名稱里無數(shù)字	5	15	20
總計(jì)	20	20	40

α	0.10	0.05	0.025	0.010	0.005	0.001
Χ_α	2.706	3.841	5.024	6.635	7.879	10.828

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2019-2020學(xué)年湖北省十堰市高三（上）期末數(shù)學(xué)試卷（文科）（元月調(diào)考）

一、選擇題：本題共12小題，每小題5分，共60分．在每小題給出的四個(gè)選項(xiàng)中，只有一項(xiàng)是符合題目要求的．

1．如圖，正方體ABCD-A1B1C1D1中，M是A1D的中點(diǎn)，則（ ）

2．已知曲線C1：y=sinx,曲線C2：y=sin（ωx+φ）（ω＞0，|φ|＜π2）的部分圖像如圖所示，則下列結(jié)論正確的是（ ）

3．若復(fù)數(shù)z滿足（1+3i）z=2+4i,則z的虛部為（ ）

4．在正三棱柱ABC-A'B'C'中，D是側(cè)棱BB'上一點(diǎn)，E是側(cè)棱CC'上一點(diǎn)，若線段AD+DE+EA'的最小值是27，且其內(nèi)部存在一個(gè)內(nèi)切球（與該棱柱的所有面均相切），則該棱柱的外接球表面積為（ ）

5．已知等軸雙曲線的焦距為8，左、右焦點(diǎn)F1，F(xiàn)2在x軸上，中心在原點(diǎn)，點(diǎn)A的坐標(biāo)為（2，23），P為雙曲線右支上一動(dòng)點(diǎn)，則|PF1|+|PA|的最小值為（ ）

6．某校初一（1）班和初一（2）班各有10人騎自行車上學(xué)，他們每天騎行路程（單位：千米）的莖葉圖如圖所示，則1班10人每天騎行路程的極差和2班10人每天騎行路程的中位數(shù)分別是（ ）

7．拋物線C：y2=-12x的焦點(diǎn)為F，P為拋物線C上一動(dòng)點(diǎn)，定點(diǎn)A（-5，2），則|PA|+|PF|的最小值為（ ）

8．已知函數(shù)f（x）=2x1+2x，則對(duì)任意實(shí)數(shù)x,有（ ）

9．已知函數(shù)f（x）的定義域?yàn)锽，函數(shù)f（1-2x）的定義域?yàn)?div id="gakugmc" class="MathJye" mathtag="math">A=[-12，12）

10．已知集合A={x|x-1＞0}，B={x|x2-2x≤0}，則A∩B=（ ）

11．已知等比數(shù)列的前n項(xiàng)和Sn=4n+a,則a的值等于（ ）

12．執(zhí)行如圖所示的程序框圖，輸出的結(jié)果為（ ）

二、填空題：本大題共4小題，每小題5分，共20分．

13．若Sn數(shù)列{an}的前n項(xiàng)和，且對(duì)任意的正整數(shù)n,有Sn=2an-1，則a1=，Sn=．

16．已知向量a，b滿足|a|=5，|b|=2，且a在b上的投影向量為2b，則a，b夾角的余弦值為 ，a?b=．

三、解答題：共70分．解答應(yīng)寫出文字說明、證明過程或演算步驟，第17～21題為必考題，每道試題考生都必須作答．第22、23題為選考題，考生根據(jù)要求作答．（一）必考題：共60分．

17．設(shè)函數(shù)f（x）=5-|x+a|-|x-2|．（1）當(dāng)a=1時(shí)，求不等式f（x）≥0的解集；（2）若f（x）≤1，求a的取值范圍．

四、選考題：共10分，請(qǐng)考生在第22、23題中任選一題作答，如果多做，則按所做的第一題計(jì)分．

23．已知橢圓C：x2a2+y2b2=1（a＞b＞0）經(jīng)過點(diǎn)M（1，22），N（2，0）．（1）求橢圓C的方程；（2）已知直線l的傾斜角為銳角，l與圓x2+y2=12相切，與橢圓C交于A、B兩點(diǎn)，且△AOB的面積為23，求直線l的方程．

1．如圖，正方體ABCD-A₁B₁C₁D₁中，M是A₁D的中點(diǎn)，則（　　）

2．已知曲線C₁：y=sinx,曲線C₂：
y
=
sin
（
ωx
+
φ
）
（
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分圖像如圖所示，則下列結(jié)論正確的是（　　）

3．若復(fù)數(shù)z滿足（1+3i）z=2+4i,則z的虛部為（　　）

4．在正三棱柱ABC-A'B'C'中，D是側(cè)棱BB'上一點(diǎn)，E是側(cè)棱CC'上一點(diǎn)，若線段AD+DE+EA'的最小值是
2
7
，且其內(nèi)部存在一個(gè)內(nèi)切球（與該棱柱的所有面均相切），則該棱柱的外接球表面積為（　　）

5．已知等軸雙曲線的焦距為8，左、右焦點(diǎn)F₁，F(xiàn)₂在x軸上，中心在原點(diǎn)，點(diǎn)A的坐標(biāo)為
（
2
，
2
3
）
，P為雙曲線右支上一動(dòng)點(diǎn)，則|PF₁|+|PA|的最小值為（　　）

6．某校初一（1）班和初一（2）班各有10人騎自行車上學(xué)，他們每天騎行路程（單位：千米）的莖葉圖如圖所示，則1班10人每天騎行路程的極差和2班10人每天騎行路程的中位數(shù)分別是（　　）

7．拋物線C：y²=-12x的焦點(diǎn)為F，P為拋物線C上一動(dòng)點(diǎn)，定點(diǎn)A（-5，2），則|PA|+|PF|的最小值為（　　）

8．已知函數(shù)f（x）=
2
x
1
+
2
x
，則對(duì)任意實(shí)數(shù)x,有（　　）

9．已知函數(shù)f（x）的定義域?yàn)锽，函數(shù)f（1-2x）的定義域?yàn)?div id="gakugmc" class="MathJye" mathtag="math">
A
=
[
-
1
2
，
1
2
）

10．已知集合A={x|x-1＞0}，B={x|x²-2x≤0}，則A∩B=（　　）

11．已知等比數(shù)列的前n項(xiàng)和S_n=4ⁿ+a,則a的值等于（　　）

12．執(zhí)行如圖所示的程序框圖，輸出的結(jié)果為（　　）

13．若S_n數(shù)列{a_n}的前n項(xiàng)和，且對(duì)任意的正整數(shù)n,有S_n=2a_n-1，則a₁=
，S_n=
．

16．已知向量
a
，
b
滿足
|
a
|
=
5
，
|
b
|
=
2
，且
a
在
b
上的投影向量為
2
b
，則
a
，
b
夾角的余弦值為
，
a
?
b
=
．

17．設(shè)函數(shù)f（x）=5-|x+a|-|x-2|．
（1）當(dāng)a=1時(shí)，求不等式f（x）≥0的解集；
（2）若f（x）≤1，求a的取值范圍．