當前位置：試卷中心 > 試卷詳情

2021-2022學年遼寧省沈陽市重點高中聯合體高二（上）月考數學試卷（12月份）

發布：2025/11/13 13:0:26

一、單選題（本大題共8個小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合要求的。）

1．古希臘數學家阿波羅尼斯與歐幾里得、阿基米德齊名，他發現：“平面內到兩個定點A，B的距離之比為定值m（m≠1）的點的軌跡是圓”．人們將這個圓以他的名字命名為阿波羅尼斯圓，簡稱阿氏圓．在平面直角坐標系xOy中，A（-2，0），B（4，0），點P滿足
|
PA
|
|
PB
|
=
1
2
．設點P的軌跡為C，則下列結論正確的是（　　）
A．圓C的方程為（x+4）²+y²=12
B．軌跡圓C的面積為12π
C．在C上存在K使得|KO|=2|KA|
D．當A，B，P三點不共線時，射線PO是∠APB的平分線
組卷：94引用：5難度：0.6
2．已知F₁，F₂是橢圓
x
2
25
+
y
2
16
=
1
的兩個焦點，P是橢圓上一點，則|PF₁|?|PF₂|的最大值是（　　）
A．
25
4
B．9 C．16 D．25
組卷：1299引用：10難度：0.7
3．已知直線x+my-2=0與直線y=nx垂直，則m,n的關系為（　　）
A．mn-1=0 B．mn+1=0 C．m-n=0 D．m+n+1=0
組卷：38引用：3難度：0.7
4．下列各個圖形中，異面直線的畫法不妥的是（　　）
A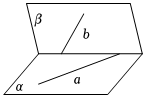． B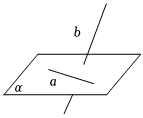． C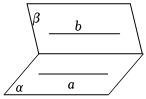． D．
組卷：132引用：3難度：0.9
5．已知直線y=kx+t與圓x²+（y+1）²=1相切且與拋物線C：x²=4y交于不同的兩點M，N，則實數t的取值范圍是（　　）
A．（-∞，-3）∪（0，+∞） B．（-∞，-2）∪（0，+∞）
C．（-3，0） D．（-2，0）
組卷：51引用：1難度：0.5
6．放假伊始，8名同學相約前往某門店體驗沉浸式角色扮演型劇本游戲，目前店中僅有可供4人組局的劇本，其中A，B角色各1人，C角色2人．已知這8名同學中有4名男生，4名女生，店主讓他們8人分成兩組先后參加游戲，其中A，B角色不可同時為女生，C角色至少有一名女生，則他們不同的選擇方式共有（　　）
A．2376種 B．4752種 C．9504種 D．1584種
組卷：104引用：5難度：0.6
7．某市為了實施教育振興計劃，依托本市一些優質教育資源，每年都對本市所有在高校就讀的定向師范生實施教育教學技能培訓，以提高定向師范生的畢業質量．現有5名即將畢業的定向師范生擬分配到3所學校進行跟崗培訓，每名師范生只能跟崗1所學校，每所學校至少分配1名師范生，則不同的跟崗分配方案共有（　　）
A．150種 B．300種 C．360種 D．540種
組卷：54引用：3難度：0.8
8．已知F₁，F₂是橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的兩個焦點，P為C上一點，且∠F₁PF₂=60°，|PF₁|=3|PF₂|，則C的離心率為（　　）
A．
2
2
B．
21
6
C．
7
4
D．
2
3
組卷：690引用：3難度：0.7

二、多選題（本大題共4個小題，每小題5分，共計20分。在每小題給出的選項中有多項符合題目要求，全部選對得5分，部分選對得2分，錯選或者多選不得分。）

9．已知雙曲線C：x²-
y
2
3
=1，F₁，F₂為雙曲線的左、右焦點，若直線l過點F₂，且與雙曲線的右支交于M，N兩點，下列說法正確的是（　　）
A．雙曲線C的離心率為
3
B．若l的斜率為2，則MN的中點為（8，12）
C．若∠F₁MF₂=
π
3
，則△MF₁F₂的面積為3
3
D．使△MNF₁為等腰三角形的直線l有3條
組卷：7引用：0難度：0.5
10．已知雙曲線C：
y
2
9
-
x
2
7
=
1
，則下列選項中正確的是（　　）
A．C的焦點坐標為（±4，0） B．C的頂點坐標為（0，±3）
C．C的離心率為
4
3
D．C的虛軸長為
2
7
組卷：70引用：6難度：0.6
11．已知正四面體ABCD，下列說法中正確的是（　　）
A．AB與CD垂直
B．直線AD與平面BCD所成角的正弦值為
6
3
C．平面ABD與平面ABC所成角的大小為
π
3
D．若AB=2，則直線AD與直線BC之間的距離為
2
組卷：25引用：2難度：0.5
12．已知拋物線C：x²=2y的焦點為F，準線為l,直線y=kx+m與C相交于A，B兩點，M為AB的中點，則（　　）
A．若m=2，則∠AOB=90°
B．若
3
AF
=
7
FB
，則直線AB的斜率為
2
21
21
C．△OBF不可能是正三角形
D．當AB=4時，點M到l的距離的最小值為2
組卷：80引用：2難度：0.5

三、填空題（本大題共4個小題，每題5分，共計20分。）

13．用0，1，2，3，4，5，6七個數共可以組成

個沒有重復數字的三位數．
組卷：516引用：4難度：0.7
14．方程
x
2
m
-
2
+
y
2
m
-
6
=1表示橢圓，則該橢圓的焦點坐標是
．
組卷：40引用：1難度：0.6
15．過拋物線y²=2px（p＞0）的焦點F作直線l,交拋物線于A、B兩點，交其準線于C點，若
CB
=
3
BF
，則直線l的斜率為
．
組卷：55引用：4難度：0.7
16．若橢圓
2
x
2
a
2
+
y
2
a
2
=
1
與以A（1，2）、B（2，3）為端點的線段AB無交點，則正實數a的范圍是
．
組卷：10引用：0難度：0.7

四、解答題（本大題共6個小題，共計70分，解答應寫出文字說明、證明過程或演算步驟，并寫在答題卡相應位置上。）

17．求下列方程中的n值．
（1）
A
3
2
n
=
2
A
4
n
+
1
；
（2）
C
n
-
2
n
+
2
+
C
n
-
3
n
+
2
=
1
10
A
3
n
+
3
．
組卷：138引用：2難度：0.7
18．已知圓C過點M（0，-1）且與圓C₁：
x
2
+
y
2
-
2
2
x
-
2
2
y
+
3
=
0
相切于點
N
（
2
2
，
2
2
）
，直線l：kx-y-k+3=0與圓C交于不同的兩點A，B．
（1）求圓C的方程；
（2）若圓C與x軸的正半軸交于點P，直線PA，PB的斜率分別為k₁，k₂，求k₁+k₂的值．
組卷：54引用：5難度：0.5
19．3名女生和4名男生站成一排照相．
（1）共有多少種不同的站法？
（2）4名男生全部相鄰的站法有多少種？
（3）若甲是女生，甲既不站排頭也不站排尾，則女生互不相鄰的站法有多少種？
組卷：9引用：0難度：0.8
20．已知
F
（
1
2
，
0
）
為拋物線y²=2px（p＞0）的焦點，點N（x₀，y₀）（y₀＞0）為其上一點，M與N關于x軸對稱，直線l與拋物線交于異于M、N的A、B兩點，
|
NF
|
=
5
2
，K_NA?K_NB=-2．
（Ⅰ）求拋物線的標準方程和N點的坐標；
（Ⅱ）判斷是否存在這樣的直線l,使得△MAB的面積最小．若存在，求出直線l的方程和△MAB面積的最小值；若不存在，請說明理由．
組卷：136引用：2難度：0.5
21．如圖，四棱錐P-ABCD的底面是等腰梯形，AD∥BC，BC=2AB=2AD=2，PC=
3
，PC⊥底面ABCD，M為棱AP上的一點．
（1）證明：AB⊥CM；
（2）若二面角A-DC-M的余弦值為
17
17
，求
PM
PA
的值．
組卷：222引用：6難度：0.5
22．已知橢圓C的方程為
x
2
a
2
+
y
2
3
=1（a＞0），斜率為k（k≠0）的直線與C交于M，N兩點．
（1）若G為MN的中點，O為坐標原點，且直線OG的斜率為-
3
4
k
，求橢圓C的方程；
（2）在（1）的條件下，若P是橢圓C的左頂點，直線PM的斜率為k_PM，直線PN的斜率為k_PN，k_PM?k_PN=-
1
4
，F是橢圓的左焦點，要使F在以MN為直徑的圓內，求k的取值范圍．
組卷：151引用：1難度：0.5

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．（-∞，-3）∪（0，+∞）	B．（-∞，-2）∪（0，+∞）
C．（-3，0）	D．（-2，0）

A．C的焦點坐標為（±4，0）	B．C的頂點坐標為（0，±3）
C．C的離心率為 4 3	D．C的虛軸長為 2 7

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2021-2022學年遼寧省沈陽市重點高中聯合體高二（上）月考數學試卷（12月份）

一、單選題（本大題共8個小題，每小題5分，共40分，在每小題給出的四個選項中，只有一項是符合要求的。）

2．已知F1，F2是橢圓x225+y216=1的兩個焦點，P是橢圓上一點，則|PF1|?|PF2|的最大值是（ ）

3．已知直線x+my-2=0與直線y=nx垂直，則m,n的關系為（ ）

4．下列各個圖形中，異面直線的畫法不妥的是（ ）

5．已知直線y=kx+t與圓x2+（y+1）2=1相切且與拋物線C：x2=4y交于不同的兩點M，N，則實數t的取值范圍是（ ）

8．已知F1，F2是橢圓C：x2a2+y2b2=1（a＞b＞0）的兩個焦點，P為C上一點，且∠F1PF2=60°，|PF1|=3|PF2|，則C的離心率為（ ）

二、多選題（本大題共4個小題，每小題5分，共計20分。在每小題給出的選項中有多項符合題目要求，全部選對得5分，部分選對得2分，錯選或者多選不得分。）

9．已知雙曲線C：x2-y23=1，F1，F2為雙曲線的左、右焦點，若直線l過點F2，且與雙曲線的右支交于M，N兩點，下列說法正確的是（ ）

10．已知雙曲線C：y29-x27=1，則下列選項中正確的是（ ）

11．已知正四面體ABCD，下列說法中正確的是（ ）

12．已知拋物線C：x2=2y的焦點為F，準線為l,直線y=kx+m與C相交于A，B兩點，M為AB的中點，則（ ）

三、填空題（本大題共4個小題，每題5分，共計20分。）

13．用0，1，2，3，4，5，6七個數共可以組成 個沒有重復數字的三位數．

14．方程x2m-2+y2m-6=1表示橢圓，則該橢圓的焦點坐標是．

15．過拋物線y2=2px（p＞0）的焦點F作直線l,交拋物線于A、B兩點，交其準線于C點，若CB=3BF，則直線l的斜率為．

16．若橢圓2x2a2+y2a2=1與以A（1，2）、B（2，3）為端點的線段AB無交點，則正實數a的范圍是．

四、解答題（本大題共6個小題，共計70分，解答應寫出文字說明、證明過程或演算步驟，并寫在答題卡相應位置上。）

17．求下列方程中的n值．（1）A32n=2A4n+1；（2）Cn-2n+2+Cn-3n+2=110A3n+3．

18．已知圓C過點M（0，-1）且與圓C1：x2+y2-22x-22y+3=0相切于點N（22，22），直線l：kx-y-k+3=0與圓C交于不同的兩點A，B．（1）求圓C的方程；（2）若圓C與x軸的正半軸交于點P，直線PA，PB的斜率分別為k1，k2，求k1+k2的值．

19．3名女生和4名男生站成一排照相．（1）共有多少種不同的站法？（2）4名男生全部相鄰的站法有多少種？（3）若甲是女生，甲既不站排頭也不站排尾，則女生互不相鄰的站法有多少種？

21．如圖，四棱錐P-ABCD的底面是等腰梯形，AD∥BC，BC=2AB=2AD=2，PC=3，PC⊥底面ABCD，M為棱AP上的一點．（1）證明：AB⊥CM；（2）若二面角A-DC-M的余弦值為1717，求PMPA的值．

2．已知F₁，F₂是橢圓
x
2
25
+
y
2
16
=
1
的兩個焦點，P是橢圓上一點，則|PF₁|?|PF₂|的最大值是（　　）

3．已知直線x+my-2=0與直線y=nx垂直，則m,n的關系為（　　）

4．下列各個圖形中，異面直線的畫法不妥的是（　　）

5．已知直線y=kx+t與圓x²+（y+1）²=1相切且與拋物線C：x²=4y交于不同的兩點M，N，則實數t的取值范圍是（　　）

8．已知F₁，F₂是橢圓
C
：
x
2
a
2
+
y
2
b
2
=
1
（
a
＞
b
＞
0
）
的兩個焦點，P為C上一點，且∠F₁PF₂=60°，|PF₁|=3|PF₂|，則C的離心率為（　　）

9．已知雙曲線C：x²-
y
2
3
=1，F₁，F₂為雙曲線的左、右焦點，若直線l過點F₂，且與雙曲線的右支交于M，N兩點，下列說法正確的是（　　）

10．已知雙曲線C：
y
2
9
-
x
2
7
=
1
，則下列選項中正確的是（　　）

11．已知正四面體ABCD，下列說法中正確的是（　　）

12．已知拋物線C：x²=2y的焦點為F，準線為l,直線y=kx+m與C相交于A，B兩點，M為AB的中點，則（　　）

13．用0，1，2，3，4，5，6七個數共可以組成

個沒有重復數字的三位數．

14．方程
x
2
m
-
2
+
y
2
m
-
6
=1表示橢圓，則該橢圓的焦點坐標是
．

15．過拋物線y²=2px（p＞0）的焦點F作直線l,交拋物線于A、B兩點，交其準線于C點，若
CB
=
3
BF
，則直線l的斜率為
．

16．若橢圓
2
x
2
a
2
+
y
2
a
2
=
1
與以A（1，2）、B（2，3）為端點的線段AB無交點，則正實數a的范圍是
．

17．求下列方程中的n值．
（1）
A
3
2
n
=
2
A
4
n
+
1
；
（2）
C
n
-
2
n
+
2
+
C
n
-
3
n
+
2
=
1
10
A
3
n
+
3
．

19．3名女生和4名男生站成一排照相．
（1）共有多少種不同的站法？
（2）4名男生全部相鄰的站法有多少種？
（3）若甲是女生，甲既不站排頭也不站排尾，則女生互不相鄰的站法有多少種？

21．如圖，四棱錐P-ABCD的底面是等腰梯形，AD∥BC，BC=2AB=2AD=2，PC=
3
，PC⊥底面ABCD，M為棱AP上的一點．
（1）證明：AB⊥CM；
（2）若二面角A-DC-M的余弦值為
17
17
，求
PM
PA
的值．