2023-2024學年陜西省西安市濱河學校高一(上)期中數學試卷
發布:2025/11/13 15:0:30
一、單選題。本題共8小題,每小題4分,共32分。在每一題給出的四個選項中,只有一項是符合題目要求的。
-
1.二次函數f(x)=x2+2ax-1在區間(1,+∞)上單調遞增的一個充分不必要條件為( )
組卷:96引用:2難度:0.7解析 -
2.下列結論正確的是( )
組卷:202引用:7難度:0.7解析 -
3.已知f(x)的定義域為(0,1],則f(sinx)的定義域為( )
組卷:0引用:0難度:0.7解析 -
4.已知關于x的不等式(2a+3m)x2-(b-3m)x-1>0(a>0,b>0)的解集為(-∞,-1)∪(
,+∞),則下列結論錯誤的是( )12組卷:581引用:4難度:0.5解析 -
5.已知f(x)為奇函數,且當x>0時,f(x)=x2-4x+2,則f(x)在區間[-4,-2]上( )
組卷:150引用:4難度:0.7解析 -
6.已知函數f(x-1)=x2-2x,且f(a)=3,則實數a的值等于( )
組卷:272引用:4難度:0.9解析 -
7.已知全集U={1,2,3,4,5},集合A={3,4,5},B={2,3,4},則?U(A∩B)=( )
組卷:4引用:1難度:0.7解析 -
8.若函數f(x)=(m2-6m+9)
是冪函數且為奇函數,則m的值為( )xm2-3m+1組卷:690引用:3難度:0.7解析
二、多選題。本題共4小題,每小題4分,共16分。在每小題給出的選項中,有多項符合題目要求,全部選對的得4分,部分選對的得2分,有選錯的得0分。
-
9.給出下列四個結論,其中正確的結論有( )
組卷:194引用:1難度:0.8解析 -
10.一組數據:0,1,5,6,7,11,12,則( )
組卷:54引用:11難度:0.7解析 -
11.已知函數f(x)=|ln|x+a||,則其圖象可能是( )
組卷:38引用:3難度:0.7解析 -
12.若函數f(x)在其圖象上存在不同的兩點A(x1,y1),B(x2,y2),其坐標滿足條件:
的最大值為0,則稱f(x)為“柯西函數”,則下列函數中是“柯西函數”的為( )|x1x2+y1y2|-x21+y21?x22+y22組卷:72引用:2難度:0.5解析
三、填空題。本題共4小題,每小題4分,共16分。
-
13.有理數都可以表示成
(m,n∈Z,且n≠0,m與n互質)的形式,進而有理數集可表示為mn.任何有理數,都可以化為有限小數或無限循環小數.反之,任一有限小數或無限循環小數也可以化為Q={mn|m,n∈Z,且n≠0,m與n互質}的形式,從而是有理數;那么無限循環小數mn表示成1..2的形式為 .mn組卷:99引用:1難度:0.7解析 -
14.對于任意實數x,符號[x]表示x的整數部分,即[x]是不超過x的最大整數,這個函數[x]叫做“取整函數”,則[lg1]+[lg2]+[lg3]+…+[lg2018]=.
組卷:25引用:1難度:0.7解析 -
15.已知
,則f(f(x))=2的解集為.f(x)=-log2x,x>0x+1,x≤0組卷:69引用:3難度:0.8解析 -
16.函數y=|x-1|的遞增區間是
.組卷:938引用:3難度:0.9解析
四、解答題。本題共6個小題,共56分。解答應寫出文字說明,證明過程或演算步驟。
-
17.如果函數f(x)的定義域為{x|x>0},且f(x)為增函數,f(x?y)=f(x)+f(y).
(Ⅰ)求證:f()=f(x)-f(y);xy
(Ⅱ)已知f(3)=1,且f(a)-f(a-1)>2,求a的取值范圍.組卷:63引用:7難度:0.3解析 -
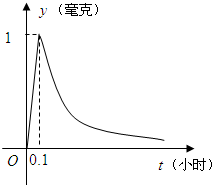 18.為了預防流感,某學校對教室用藥熏消毒法進行消毒.如圖所示,已知藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)的函數關系式為(a為常數).y=(116)t-a
18.為了預防流感,某學校對教室用藥熏消毒法進行消毒.如圖所示,已知藥物釋放過程中,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)成正比;藥物釋放完畢后,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)的函數關系式為(a為常數).y=(116)t-a
(1)求常數a的值;
(2)求從藥物釋放開始,室內每立方米空氣中的含藥量y(毫克)與時間t(小時)之間的函數關系式;
(3)當藥物釋放完畢后,規定空氣中每立方米的含藥量不大于0.25毫克時,學生方可進入教室.問從藥物釋放開始,至少需要經過多少小時,學生才能回到教室?組卷:24引用:1難度:0.3解析 -
19.已知集合A={x|3≤3x≤27},B={x|log2x>1}.
(1)求A∩(?RB);
(2)已知集合C={x|1<x<a},若C∩A=C,求實數a的取值集合.組卷:256引用:7難度:0.5解析 -
20.已知函數
是定義在[n-3,2n]上的奇函數.f(x)=3x+m3x+1
(Ⅰ)求m,n的值;
(Ⅱ)證明:函數f(x)是增函數;
(Ⅲ)若f(a2)+f(-3a-4)<0,求實數a的取值范圍.組卷:150引用:2難度:0.6解析 -
21.已知函數f(x)=x2+4x+3
(1)若g(x)=f(x)+bx為偶函數,求b的值.
(2)求f(x)在[-3,3]上的最值.組卷:6引用:2難度:0.7解析 -
22.解不等式組
,并將解集在數軸上表示出來.x-5<3x-6x-2≤6-3x組卷:4引用:1難度:0.8解析


