2023-2024學年福建省莆田八中、莆田僑中聯考高一(上)期末數學試卷
發布:2025/11/13 15:0:30
一、選擇題:本題共8小題,每小題5分,共40分.在每小題給出的四個選項中,只有一項是符合題目要求.
-
1.函數
的最小正周期和振幅分別是( )f(x)=3sinxcosx+12cos2xA.π,1 B.π,2 C.2π,1 D.2π,2 組卷:19引用:2難度:0.7解析 -
2.定義在R上的函數f(x),滿足f(x)=
,且f(x+1)=f(x-1),若g(x)=3-log2x,則函數F(x)=f(x)-g(x)在(0,+∞)內的零點個數有( )x2+2,x∈[0,1)2-x2,x∈[-1,0)A.3個 B.2個 C.1個 D.0個 組卷:270引用:3難度:0.7解析 -
3.“x-1>0”是“x2-1>0”的( )
A.充分不必要條件 B.必要不充分條件 C.充分必要條件 D.既不充分也不必要條件 組卷:176引用:5難度:0.7解析 -
4.在下列冪函數中:y=x,y=x
,y=x12,y=x23,y=x13,y=x-2,在(0,+∞)上是增函數的個數為( )-13A.2個 B.3個 C.4個 D.5個 組卷:15引用:1難度:0.7解析 -
5.已知角α頂點在坐標原點,始邊與x軸非負半軸重合,終邊過點P(3,-4),將α的終邊逆時針旋轉180°,這時終邊所對應的角是β,則cosβ=( )
A. -45B. -35C. 35D. 45組卷:278引用:5難度:0.7解析 -
6.已知α∈(0,π),若cosα=-
,則tanα的值為( )12A. 33B.- 33C. 3D.- 3組卷:871引用:4難度:0.9解析 -
7.已知集合
,B={x|x2-x-6<0},則A∩?RB=( )A={x|18<2x<8)A.{x|-2<x<3} B.{x|-3<x<2} C.? D.{x|-3<x≤-2} 組卷:15引用:1難度:0.7解析 -
8.定義函數f(x)=
,則函數g(x)=xf(x)-6在區間[1,2n](n∈N*)內的所有零點的和為( )4-8|x-32|,1≤x≤212f(x2),x>2A.n B.2n C. (2n-1)34D. (2n-1)32組卷:246引用:16難度:0.5解析
二、多選題(本題共4小題,每小題5分,共20分,在每小題給出的選項中,有多項符合題目要求.全部選對的得5分,部分選對的得2分,有選錯的得0分)
-
9.下列各組函數中,表示同一函數的是( )
A.y=x-2, y=x2x-2B. ,y=x2-2y=x4-4x2+2C.y=2x-5, y=(2x-5)2D. ,y=2x-1?2x+1y=4x-1組卷:36引用:4難度:0.8解析 -
10.已知直線y=-x+2分別與函數y=ex和y=lnx的圖像交于點A(x1,y1)B(x2,y2),則下列說法正確的是( )
A.x1+x2=2 B. +ex1>2eex2C. +ln(2x2)<2ex1D.x1x2< e2組卷:34引用:1難度:0.5解析 -
11.已知x2(y2+1)=4,則( )
A.xy<2 B.x2y≥-1 C.x+xy≤2 2D.x2+xy≤ 174組卷:57引用:1難度:0.5解析 -
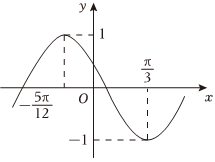 12.已知函數f(x)=sin(ωx+φ)(ω>0,|φ|<π)的的部分圖象如圖所示,則下列說法中正確的是( )
12.已知函數f(x)=sin(ωx+φ)(ω>0,|φ|<π)的的部分圖象如圖所示,則下列說法中正確的是( )A.f(x)的最小正周期為π B.f(x)的圖象關于 對稱(7π12,0)C.f(x)在 上為減函數[-5π6,-π2]D.把f(x)的圖象向右平移 個單位長度可得一個偶函數的圖象5π12組卷:87引用:4難度:0.7解析
三、填空題(本題共4小題,每小題5分,共20分)
-
13.如果x∈(0,2π),則函數y=
+sinx的定義域對應的區間是-tanx.組卷:16引用:1難度:0.7解析 -
14.函數f(x)=3sin(2x-
)的圖象為C,則以下結論中正確的是.(寫出所有正確結論的編號).π3
①圖象C關于直線x=對稱;π12
②圖象C關于點對稱;(2π3,0)
③函數f(x)在區間(-,π12)內是增函數;5π12
④由y=3sin2x的圖象向右平移個單位長度可以得到圖象C.π3組卷:141引用:8難度:0.5解析 -
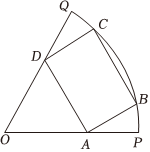 15.如圖,在扇形OPO中,半徑OP=1,圓心角,矩形ABCD內接于扇形OPQ,其中點B,C都在弧PQ上,則矩形ABCD的面積的最大值為 .∠POQ=π3組卷:174引用:3難度:0.6
15.如圖,在扇形OPO中,半徑OP=1,圓心角,矩形ABCD內接于扇形OPQ,其中點B,C都在弧PQ上,則矩形ABCD的面積的最大值為 .∠POQ=π3組卷:174引用:3難度:0.6解析 -
16.已知函數
,x∈R(a為常數)在區間[2,+∞)上是增函數,則實數a的取值范圍是.f(x)=3x2-ax組卷:53引用:2難度:0.6解析
四、解答題:本題共6小題,共70分,解答應寫出文字說明、證明過程或演算步驟.
-
17.已知函數
是定義域在(-2,2)上的奇函數.f(x)=ax2+x+b+1x2+1
(1)求a,b;
(2)判斷f(x)在(0,2)上的單調性,并予以證明.
(3)函數,若g(x)在[m,n]上的值域是[m,n],求m,n的值.g(x)=-xf(x)+2x+1(x≥0)組卷:21引用:2難度:0.5解析 -
18.已知函數f(x)=3ax2+2bx+c,a+b+c=0,f(0)>0,f(1)>0,證明a>0,并利用二分法證明方程f(x)=0在區間[0,1]內有兩個實根.
組卷:76引用:6難度:0.6解析 -
19.已知f(α)=
.sin(5π-α)cos(72π-α)tan(-π+α)-tan(-19π-α)sin(-α)
(1)化簡f(α);
(2)若α為第二象限角,sin(+α)=π3,求f(α).45組卷:27引用:1難度:0.5解析 -
20.為了抗擊新型冠狀病毒肺炎,某醫藥公司研究出一種消毒劑,據實驗表明,該藥物釋放量f(t)(單位:mg/m3)與時間t(單位:h)的函數關系為f(t)=
,當消毒kt,0<t<121kt,t≥12后,測量得藥物釋放量等于1(mg/m3);而實驗表明,當藥物釋放量小于12(h)對人體無害.34(mg/m3)
(1)求k的值;
(2)若使用該消毒劑對房間進行消毒,求對人體有害的時間有多長?組卷:78引用:5難度:0.6解析 -
21.已知函數
.f(x)=sinxcosx+32cos2x+12
(1)求f(x)的最小正周期;
(2)當,求f(x)的最大值.x∈[0,π4]組卷:74引用:2難度:0.5解析 -
22.已知
,sinα=45,α∈(0,π2),求cos(α-β)的值.cosβ=-513組卷:162引用:2難度:0.7解析


