精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

當前位置：試卷中心 > 試卷詳情

2024-2025學年云南大學附中星耀學校高一（下）開學數學試卷

發布：2025/11/13 16:0:33

一、選擇題：本大題共8小題，每小題5分，共40分。在每小題所給的四個選項中，有且只有一項是符合題目要求的。

1．函數y=
（
sin
2
x
2
-
cos
2
x
2
）
?
ln
|
x
|
的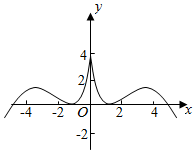圖象可能是（　　）
A． B．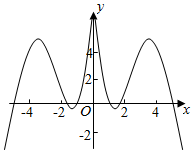
C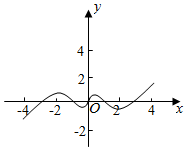． D．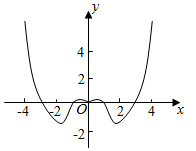
組卷：172引用：3難度：0.6
2．已知集合A={-1，0，2}，B={0，1，2}，則A∪B=（　　）
A．{-1，0，1，2} B．{-1，0，1} C．{0，1，2} D．{0，2}
組卷：271引用：3難度：0.9
3．已知a=4log₂e,b=6log₃e,c=10log₅e,e為自然對數的底數，則（　　）
A．c＞a＞b B．a＞c＞b C．b＞a＞c D．a＞b＞c
組卷：119引用：4難度：0.6
4．已知函數y=f（x）是定義在R上的偶函數，對任意x₁，x₂∈[0，+∞），且x₁≠x₂，都有
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＞
0
成立，若a=f（log₁₅3?log₁₅5），
b
=
f
（
cos
11
π
4
）
，c=f（5^0.1），則（　　）
A．a＜b＜c B．b＜a＜c C．c＜a＜b D．a＜c＜b
組卷：60引用：3難度：0.5
5．古希臘數學家阿波羅尼斯在其巨著《圓錐曲線論》中提出“在同一平面上給出三點，若其中一點到另外兩點的距離之比是一個大于零且不等于1的常數，則該點軌跡是一個圓”．現在，某電信公司要在甲、乙、丙三地搭建三座5G信號塔來構建一個特定的三角形信號覆蓋區域，以實現5G商用，已知甲、乙兩地相距4km,丙、甲兩地距離是丙、乙兩地距離的
3
倍，則這個三角形信號覆蓋區域的最大面積（單位：km²）是（　　）
A．
2
3
B．
4
3
C．
3
6
D．
4
6
組卷：77引用：3難度：0.5
6．計算：sin43°cos13°-sin13°cos43°的值等于（　　）
A．
3
B．
3
2
C．
2
2
D．
1
2
組卷：90引用：17難度：0.9
7．直線y=x-b與曲線
x
=
4
-
y
2
有且僅有一個公共點，則實數b的取值范圍為（　　）
A．
{
-
2
2
，
2
2
}
B．
（
-
2
，
2
]
∪
{
2
2
}
C．
[
-
2
，
2
2
）
∪
{
2
2
}
D．
[
-
2
，
2
）
∪
{
2
2
}
組卷：315引用：8難度：0.5
8．已知函數f（x）的定義域和值域都是集合{-1，0，1，2}，其定義如表所示，則f[f（1）]=（　　）

x -1 0 1 2

f（x） 0 1 2 -1

A．-1 B．0 C．1 D．2
組卷：45引用：7難度：0.8

二、選擇題：本題共3小題，每小題6分，共18分。在每小題給出的選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。

9．已知函數
f
（
x
）
=
sin
（
ωx
-
π
3
）
（
ω
∈
N
*
）
的圖象在（0，π）內恰有2個零點，則（　　）

A．ω=2

B．直線

是f（x）圖象的一條對稱軸

C．函數f（x）在區間為

[

，-

]

上單調遞增

D．將函數g（x）=cos2x的圖象向左平移

個單位得到函數f（x）的圖象

組卷：62引用：3難度：0.5

10．已知函數f（x）=
|
lo
g
5
（
1
-
x
）
|
，
x
＜
1
-
（
x
-
2
）
2
+
2
，
x
≥
1
，則方程f（x+
1
x
-2）=a（a∈R）的實數根個數可能為（　　）
A．5個 B．6個 C．7個 D．8個
組卷：159引用：6難度：0.3
11．下列條件可以作為x²＜1的充分不必要條件的有（　　）
A．x＜1 B．x=0 C．x＞-1 D．-1＜x＜0
組卷：116引用：8難度：0.8

三、填空題：本題共3小題，每小題5分，共15分。

12．若關于x的方程2cos2x-4sinx+4k+5=0有解，則實數k的取值范圍是
．
組卷：35引用：3難度：0.5
13．設函數
f
（
x
）
=
lo
g
3
x
,
（
x
＞
0
）
2
x
-
1
，
（
x
≤
0
）
，則f（f（1））=
．
組卷：13引用：1難度：0.7
14．冪函數
f
（
x
）
=
x
3
2
的定義域為
．
組卷：18引用：1難度：0.7

四、解答題：本大題共5小題，共77分。解答時應寫出必要的文字說明、證明過程或演算步驟。

15．（1）在①
z
+
z
=
-
8
，②z為純虛數，③z為非零實數這三個條件中任選一個，補充在下面的問題中，并對其求解．
已知復數z=（m²-2m-3）+（m²-3m-4）i（i為虛數單位），若____，求實數m的值．
（2）已知x=1-i是關于x的實系數一元二次方程x²+ax+b=0的一個根，求a,b的值．
組卷：33引用：2難度：0.7
16．某醫學研究所研發一種藥物，據監測，如果成人在2h內按規定的劑量注射該藥，在注射期間，血液中的藥物含量呈線性增加；停止注射后，血液中的藥物含量呈指數衰減，每毫升血液中的藥物含量y（μg）與服藥后的時間t（h）之間近似滿足如圖所示的曲線，其中OA是線段，曲線段AB是函數y=ka^t（t≥2，a＞0，k,a是常數）的圖象，且A（2，4），B（3，2）．
（1）寫出注射該藥后每毫升血液中藥物含量y關于時間t的函數關系式；
（2）據測定：每毫升血液中藥物含量不少于0.5kg時治療有效，如果某人第一次注射藥物為早上8點，為保持療效，第二次注射藥物最遲是當天幾點鐘？
（3）若按（2）中的最遲時間注射第二次藥物，則第二次開始注射到達1.5h時，此刻該人每毫升血液中藥物含量為多少μg？（參考數據：
2
≈1.4）
組卷：50引用：4難度：0.6
17．已知函數
f
（
x
）
=
x
-
1
x
．
（Ⅰ）判斷f（x）的奇偶性；
（Ⅱ）證明：f（x）在區間（0，+∞）上單調遞增；
（Ⅲ）求函數f（x）在區間[-3，-1]上的最小值．
組卷：86引用：4難度：0.6
18．已知函數
f
（
x
）
=
6
x
+
b
x
2
+
a
為定義在R上的奇函數，且
f
（
1
）
=
3
2
．
（1）求函數f（x）的解析式；
（2）若?x∈[1，3]，使得不等式|f（x）-m|≤1成立，求實數m的取值范圍；
（3）若?n∈[0，1]，?t∈（0，+∞），使得不等式
f
（
t
）
+
nf
（
t
3
）
-
s
≤
0
成立，求實數s的最小值．
組卷：150引用：4難度：0.5
19．已知cos（α-β）=-
5
13
，cosβ=
4
5
，α∈（
π
2
，π），β∈（0，
π
2
），求cos（α-2β）的值．
組卷：161引用：4難度：0.7

0/60 進入組卷

0/20 進入試卷籃

布置作業 發布測評 反向細目表 平行組卷 下載答題卡 試卷分析 在線訓練 收藏試卷

充值會員，資源免費下載

A．	B．
C．	D．

x	-1	0	1	2
f（x）	0	1	2	-1

精品午夜寂寞影院在线观看_一本久道久久综合多人_日本视频在线观看免费_亚洲免费二区

2024-2025學年云南大學附中星耀學校高一（下）開學數學試卷

一、選擇題：本大題共8小題，每小題5分，共40分。在每小題所給的四個選項中，有且只有一項是符合題目要求的。

1．函數y=（sin2x2-cos2x2）?ln|x|的圖象可能是（ ）

2．已知集合A={-1，0，2}，B={0，1，2}，則A∪B=（ ）

3．已知a=4log2e,b=6log3e,c=10log5e,e為自然對數的底數，則（ ）

4．已知函數y=f（x）是定義在R上的偶函數，對任意x1，x2∈[0，+∞），且x1≠x2，都有f（x1）-f（x2）x1-x2＞0成立，若a=f（log153?log155），b=f（cos11π4），c=f（50.1），則（ ）

6．計算：sin43°cos13°-sin13°cos43°的值等于（ ）

7．直線y=x-b與曲線x=4-y2有且僅有一個公共點，則實數b的取值范圍為（ ）

8．已知函數f（x）的定義域和值域都是集合{-1，0，1，2}，其定義如表所示，則f[f（1）]=（ ） x -1 0 1 2 f（x） 0 1 2 -1

二、選擇題：本題共3小題，每小題6分，共18分。在每小題給出的選項中，有多項符合題目要求。全部選對的得6分，部分選對的得部分分，有選錯的得0分。

9．已知函數f（x）=sin（ωx-π3）（ω∈N*）的圖象在（0，π）內恰有2個零點，則（ ）

10．已知函數f（x）=|log5（1-x）|，x＜1-（x-2）2+2，x≥1，則方程f（x+1x-2）=a（a∈R）的實數根個數可能為（ ）

11．下列條件可以作為x2＜1的充分不必要條件的有（ ）

三、填空題：本題共3小題，每小題5分，共15分。

12．若關于x的方程2cos2x-4sinx+4k+5=0有解，則實數k的取值范圍是．

13．設函數f（x）=log3x,（x＞0）2x-1，（x≤0），則f（f（1））=．

14．冪函數f（x）=x32的定義域為 ．

四、解答題：本大題共5小題，共77分。解答時應寫出必要的文字說明、證明過程或演算步驟。

17．已知函數f（x）=x-1x．（Ⅰ）判斷f（x）的奇偶性；（Ⅱ）證明：f（x）在區間（0，+∞）上單調遞增；（Ⅲ）求函數f（x）在區間[-3，-1]上的最小值．

19．已知cos（α-β）=-513，cosβ=45，α∈（π2，π），β∈（0，π2），求cos（α-2β）的值．

1．函數y=
（
sin
2
x
2
-
cos
2
x
2
）
?
ln
|
x
|
的圖象可能是（　　）

2．已知集合A={-1，0，2}，B={0，1，2}，則A∪B=（　　）

3．已知a=4log₂e,b=6log₃e,c=10log₅e,e為自然對數的底數，則（　　）

4．已知函數y=f（x）是定義在R上的偶函數，對任意x₁，x₂∈[0，+∞），且x₁≠x₂，都有
f
（
x
1
）
-
f
（
x
2
）
x
1
-
x
2
＞
0
成立，若a=f（log₁₅3?log₁₅5），
b
=
f
（
cos
11
π
4
）
，c=f（5^0.1），則（　　）

6．計算：sin43°cos13°-sin13°cos43°的值等于（　　）

7．直線y=x-b與曲線
x
=
4
-
y
2
有且僅有一個公共點，則實數b的取值范圍為（　　）

8．已知函數f（x）的定義域和值域都是集合{-1，0，1，2}，其定義如表所示，則f[f（1）]=（　　）

x -1 0 1 2

f（x） 0 1 2 -1

9．已知函數
f
（
x
）
=
sin
（
ωx
-
π
3
）
（
ω
∈
N
*
）
的圖象在（0，π）內恰有2個零點，則（　　）

10．已知函數f（x）=
|
lo
g
5
（
1
-
x
）
|
，
x
＜
1
-
（
x
-
2
）
2
+
2
，
x
≥
1
，則方程f（x+
1
x
-2）=a（a∈R）的實數根個數可能為（　　）

11．下列條件可以作為x²＜1的充分不必要條件的有（　　）

12．若關于x的方程2cos2x-4sinx+4k+5=0有解，則實數k的取值范圍是
．

13．設函數
f
（
x
）
=
lo
g
3
x
,
（
x
＞
0
）
2
x
-
1
，
（
x
≤
0
）
，則f（f（1））=
．

14．冪函數
f
（
x
）
=
x
3
2
的定義域為
．

17．已知函數
f
（
x
）
=
x
-
1
x
．
（Ⅰ）判斷f（x）的奇偶性；
（Ⅱ）證明：f（x）在區間（0，+∞）上單調遞增；
（Ⅲ）求函數f（x）在區間[-3，-1]上的最小值．

19．已知cos（α-β）=-
5
13
，cosβ=
4
5
，α∈（
π
2
，π），β∈（0，
π
2
），求cos（α-2β）的值．